13.3.2等边三角形(2)课件 (共23张PPT)
文档属性
| 名称 | 13.3.2等边三角形(2)课件 (共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 22:25:01 | ||
图片预览





文档简介
(共23张PPT)
人教版 八年级上册
13. 3.2 等边三角形(2)
教学目标
1.探究有一个锐角等于30°的直角三角形的性质,并能运用这一性质解决问题;
2.经历对有一个锐角等于30°的直角三角形的性质的探索过程,培养学生的自主探究能力.
教学重点:有一个锐角等于30°的直角三角形的特殊性质;
教学难点:有一个锐角等于30°的直角三角形的性质的应用.
1.等边三角形三个内角都相等,并且每一个内角都等60°.
2.等边三角形是轴对称图形,有三条对称轴.中线 (角平分线,高)所在的直线就是它的对称轴.
3. 三个角都相等的三角形是等边三角形.
4.有一个角是60°的等腰三角形是等边三角形.
复习旧知
问题 已知△ABC 中,∠A =60°,( ).请你在括号内补充一个条件,使△ABC 能成为等边三角形.
∠B =60°
A
B
C
∠C =60°
AB =BC
AC =BC
AB =AC
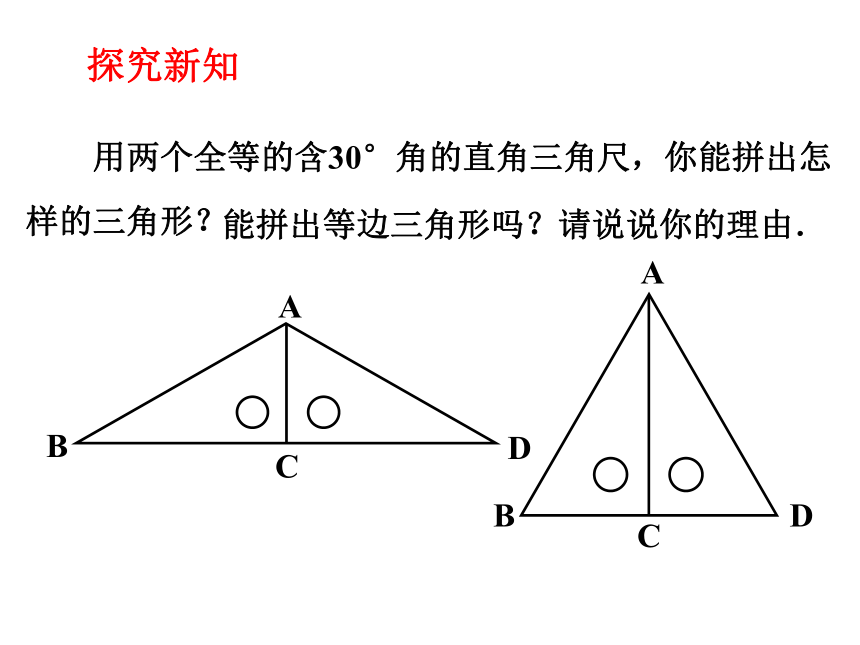
用两个全等的含30°角的直角三角尺,你能拼出怎
样的三角形?
A
B
D
C
A
B
C
D
能拼出等边三角形吗?请说说你的理由.
探究新知
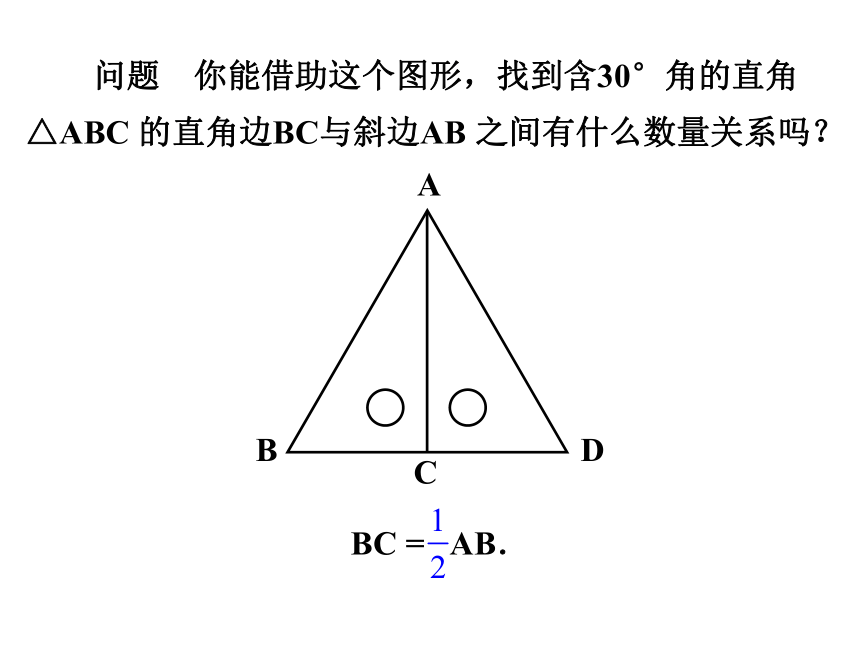
BC = AB.
问题 你能借助这个图形,找到含30°角的直角
△ABC 的直角边BC与斜边AB 之间有什么数量关系吗?
A
B
D
C
思考 这个命题是真命题吗?请进行证明.
问题 请说一说你猜想的命题中,条件和结论分别是什么?并结合图形,用符号语言表述出来.
猜想 在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
直角三角形中一个锐角等于30°,
30°锐角所对的直角边等于斜边的一半.
条件:
结论:
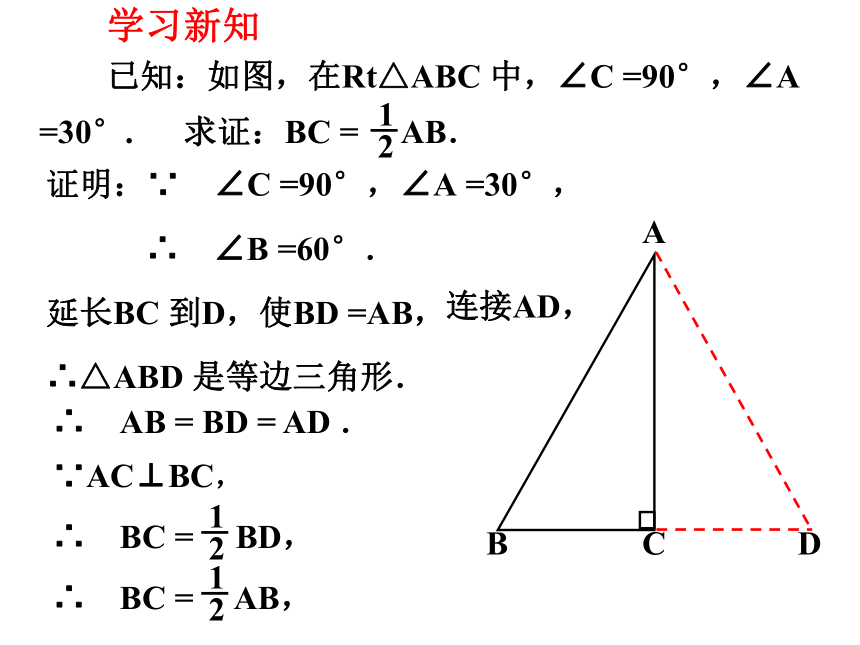
学习新知
证明:∵ ∠C =90°,∠A =30°,
∴ ∠B =60°.
延长BC 到D,使BD =AB,
∴△ABD 是等边三角形.
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB.
A
B
C
D
1
2
∴ AB = BD = AD .
∴ BC = BD,
∴ BC = AB,
1
2
1
2
∵AC⊥BC,
连接AD,
学习新知
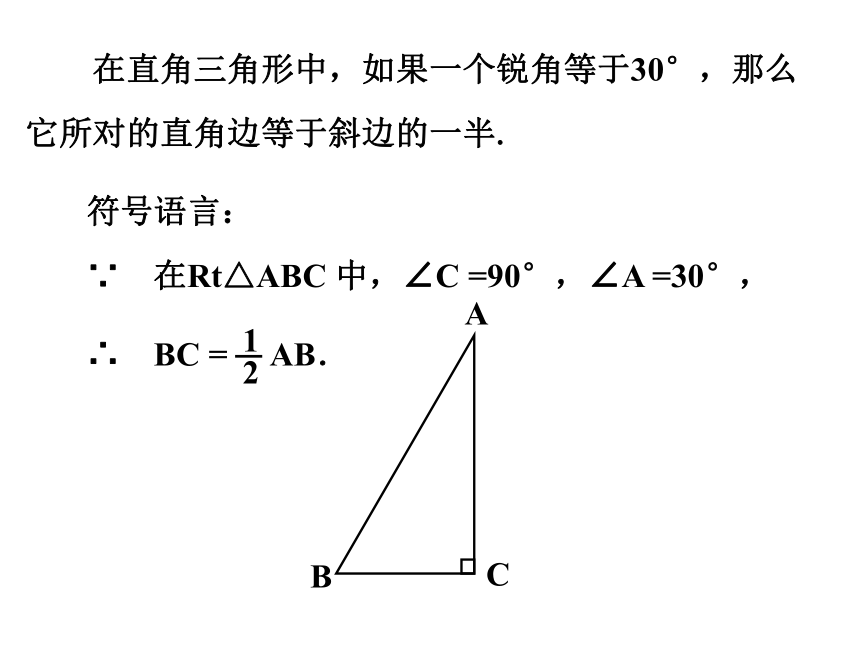
符号语言:
∵ 在Rt△ABC 中,∠C =90°,∠A =30°,
在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半.
A
B
C
∴ BC = AB.
1
2
1.如图,在△ABC 中,∠C =90°,∠A = 30°,
AB =10,则BC 的长为 .
5
A
B
C
练习巩固
2.如图,在△ABC 中,∠ACB =90°,CD 是 高,∠A =30°,AB =4.则BD = .
1
A
B
C
D
图中BC、DE 分别是哪个直角三角形的直角边?
例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长?
A
B
C
D
E
它们所对的锐角分别是多少度?
例题解析
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,
∵AD = AB,
∴ DE = AD =1.85(m) .
∴ BC =3.7(m).
答:立柱BC 的长是3.7 m,DE 的长是1.85 m.
例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长?
A
B
C
D
E
DE = AD
1
2
1
2
1
2
1
2
3. Rt△ABC 中,∠C =90°,∠B =2∠A,
∠B 和∠A 各是多少度?边AB 与BC 之间有什么关系?
A
B
C
∵∠C =90°,
∴∠A +∠B =90°.
∵∠B =2∠A ,
∴∠A =30°,
∴∠B =60°.
∴ BC = AB
1
2
解:
练习巩固
4.如图, ∠C=90°,D是CA的延长线上一点,∠D=15 °,且AD=AB,则BC= AD.
B
C
A
D
1
2
∵AB =AD,
∴∠ABD =∠D =15°,
∴∠CAB =∠ABD +∠D=30°.
5.如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=14.4cm,则AD= cm.
A
B
C
D
4.8
∵AB =AC,
∴∠B =∠C =30°,
∴∠DAC =30°,
∵DA⊥BA,
∴∠DAB =90°,
∴∠BAC =120°,
∴∠DAC =∠C ,
∴AD=CD ,
BD=2AD ,
∴BC=BD+CD
=2AD+AD
=3AD
=14.4,
∴AD=4.8 .
6.要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
A
C
B
┓
D
E
∵ △ABC和△BDE都是等边三角形
∴AB=AC,
在△ABE和△CBD中,
AB=AC
∠ABC=∠DBE
BE=BD
∴ △ABE≌△CBD
∴AE=CD.
7.如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
证明:
BE=BD,
∠ABC=∠DBE=60°.
1.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .
A
B
C
E
D
F
巩固提高
2
2.如图, △ABC中. ∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,则AC= .
A
B
C
D
E
3
今天作业
课本P83页第13、14题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
13. 3.2 等边三角形(2)
教学目标
1.探究有一个锐角等于30°的直角三角形的性质,并能运用这一性质解决问题;
2.经历对有一个锐角等于30°的直角三角形的性质的探索过程,培养学生的自主探究能力.
教学重点:有一个锐角等于30°的直角三角形的特殊性质;
教学难点:有一个锐角等于30°的直角三角形的性质的应用.
1.等边三角形三个内角都相等,并且每一个内角都等60°.
2.等边三角形是轴对称图形,有三条对称轴.中线 (角平分线,高)所在的直线就是它的对称轴.
3. 三个角都相等的三角形是等边三角形.
4.有一个角是60°的等腰三角形是等边三角形.
复习旧知
问题 已知△ABC 中,∠A =60°,( ).请你在括号内补充一个条件,使△ABC 能成为等边三角形.
∠B =60°
A
B
C
∠C =60°
AB =BC
AC =BC
AB =AC
用两个全等的含30°角的直角三角尺,你能拼出怎
样的三角形?
A
B
D
C
A
B
C
D
能拼出等边三角形吗?请说说你的理由.
探究新知
BC = AB.
问题 你能借助这个图形,找到含30°角的直角
△ABC 的直角边BC与斜边AB 之间有什么数量关系吗?
A
B
D
C
思考 这个命题是真命题吗?请进行证明.
问题 请说一说你猜想的命题中,条件和结论分别是什么?并结合图形,用符号语言表述出来.
猜想 在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
直角三角形中一个锐角等于30°,
30°锐角所对的直角边等于斜边的一半.
条件:
结论:
学习新知
证明:∵ ∠C =90°,∠A =30°,
∴ ∠B =60°.
延长BC 到D,使BD =AB,
∴△ABD 是等边三角形.
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB.
A
B
C
D
1
2
∴ AB = BD = AD .
∴ BC = BD,
∴ BC = AB,
1
2
1
2
∵AC⊥BC,
连接AD,
学习新知
符号语言:
∵ 在Rt△ABC 中,∠C =90°,∠A =30°,
在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半.
A
B
C
∴ BC = AB.
1
2
1.如图,在△ABC 中,∠C =90°,∠A = 30°,
AB =10,则BC 的长为 .
5
A
B
C
练习巩固
2.如图,在△ABC 中,∠ACB =90°,CD 是 高,∠A =30°,AB =4.则BD = .
1
A
B
C
D
图中BC、DE 分别是哪个直角三角形的直角边?
例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长?
A
B
C
D
E
它们所对的锐角分别是多少度?
例题解析
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,
∵AD = AB,
∴ DE = AD =1.85(m) .
∴ BC =3.7(m).
答:立柱BC 的长是3.7 m,DE 的长是1.85 m.
例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长?
A
B
C
D
E
DE = AD
1
2
1
2
1
2
1
2
3. Rt△ABC 中,∠C =90°,∠B =2∠A,
∠B 和∠A 各是多少度?边AB 与BC 之间有什么关系?
A
B
C
∵∠C =90°,
∴∠A +∠B =90°.
∵∠B =2∠A ,
∴∠A =30°,
∴∠B =60°.
∴ BC = AB
1
2
解:
练习巩固
4.如图, ∠C=90°,D是CA的延长线上一点,∠D=15 °,且AD=AB,则BC= AD.
B
C
A
D
1
2
∵AB =AD,
∴∠ABD =∠D =15°,
∴∠CAB =∠ABD +∠D=30°.
5.如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=14.4cm,则AD= cm.
A
B
C
D
4.8
∵AB =AC,
∴∠B =∠C =30°,
∴∠DAC =30°,
∵DA⊥BA,
∴∠DAB =90°,
∴∠BAC =120°,
∴∠DAC =∠C ,
∴AD=CD ,
BD=2AD ,
∴BC=BD+CD
=2AD+AD
=3AD
=14.4,
∴AD=4.8 .
6.要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
A
C
B
┓
D
E
∵ △ABC和△BDE都是等边三角形
∴AB=AC,
在△ABE和△CBD中,
AB=AC
∠ABC=∠DBE
BE=BD
∴ △ABE≌△CBD
∴AE=CD.
7.如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
证明:
BE=BD,
∠ABC=∠DBE=60°.
1.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .
A
B
C
E
D
F
巩固提高
2
2.如图, △ABC中. ∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,则AC= .
A
B
C
D
E
3
今天作业
课本P83页第13、14题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
