10.3实数(2)[下学期]
文档属性
| 名称 | 10.3实数(2)[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-31 00:00:00 | ||
图片预览




文档简介
课件22张PPT。10.3实数(2)
问题:每个有理数都可以用数轴上的点来表示.
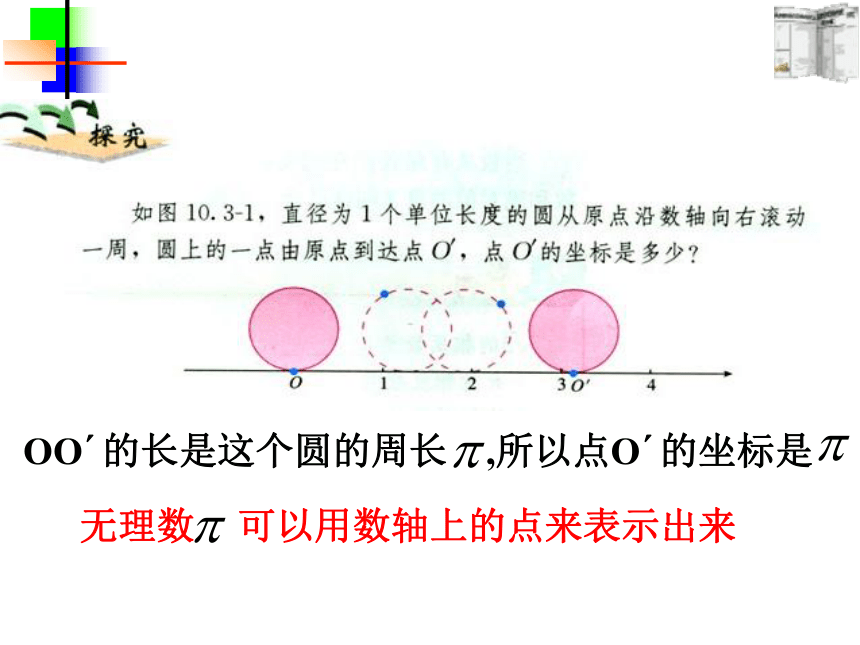
无理数是否也可以用数轴上的点来表示出来呢?OO′的长是这个圆的周长 ,所以点O′的坐标是无理数 可以用数轴上的点来表示出来(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
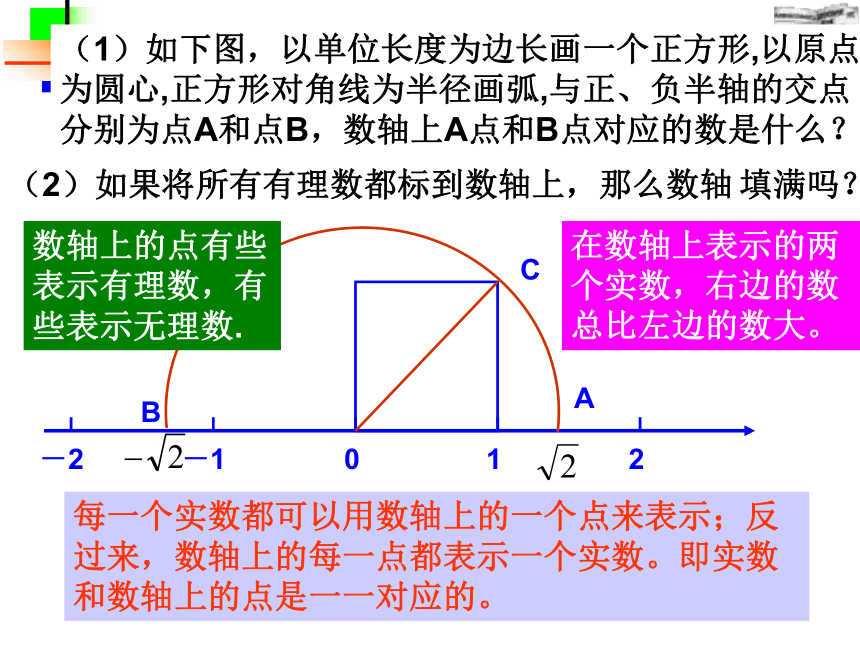
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数,右边的数总比左边的数大。数轴上的点有些
表示有理数,有
些表示无理数.例1 比较下列各组数里两个数的大小随堂练习:P178解:点A表示-1.5; 点B表示 ;点C表示 ;点D表示3;点E表示 .深入探究:平面直角坐标系中的点与有序实数对之间 也存在一一对应关系吗?问:1、数从有理数扩充到实数后,我们经学过哪些运算?除法运算中除数不能为0;正数及0可以进行开平方运算任何实数都可以开立方运算有哪些规定?2、有理数满足哪些运算律?加法交换律:a+b=b+a加法结合律(a+b)+c=a+(b+c)乘法交换律ab=ba乘法结合律(ab)c=a(bc)分配律a(b+c)=ab+ac实数范围内运算与运算律仍适用例1、计算下列各式的值:(2)| |解:(分配律)(加法结合律)练习.计算解:(2)| |P178例2、计算:≈2.236+3.142≈5.38≈1.732×1.414≈2.45解:≈ ×2.24×1.41≈1.6答:?OAB的面积约是1.6.S?OAB=解:由已知可得OB= ,?OAB的OB边上的高为 变题:如图,点B的坐标为( ,0), ?OAB
面积为 ,点A的坐标为(1, y )
求A点的纵坐标.?OAB的OB边上的高为|y|.
∵S?OAB=∴ × × | y | =∴| y |=∴y =±∵点A在第一象限∴A点的纵坐标是解: (1)围成的四边形ABCD是长方形.(2)由已知AB=5-2=3,AD=(3)A、B、C、D四点的坐标分别变为(2, )、(5, )、
( 5, 0)、( 2, 0)P179四边形ABCD的面积=AB×AD =通过这节课的学习,你有哪些收获?1、判断下列说法是否正确:1. 无限小数都是无理数。( )6.无理数都是无限不循环小数。( )2.无理数都是无限小数。( )3.带根号的数都是无理数。( )5.所有的实数都可以用数轴上的点表示,反过来,数轴上所有的点都表示实数。( )7.两个无理数之积不一定是无理数。( )8.两个无理数之和一定是无理数。 ( )×××P1784.所有的有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数。 ( )×P179解:将l=0.5m代入公式t=2 ,得t≈2×3.14×0.22t≈1.4 (s)答:小重物来回摆动一次所用的时间约1.4s。P184解:将h=1.5代入公式s2=16.88h,得s2=25.32,≈5.03(km)将h=35代入公式s2=16.88h,得s2=590.8,≈24.31.03(km)解: 设圆的半径为r cm,正方形的边长为a cm.由题意,得 r2=2 , a2=2 ∴圆的周长C1=2 r =2 ∴C1
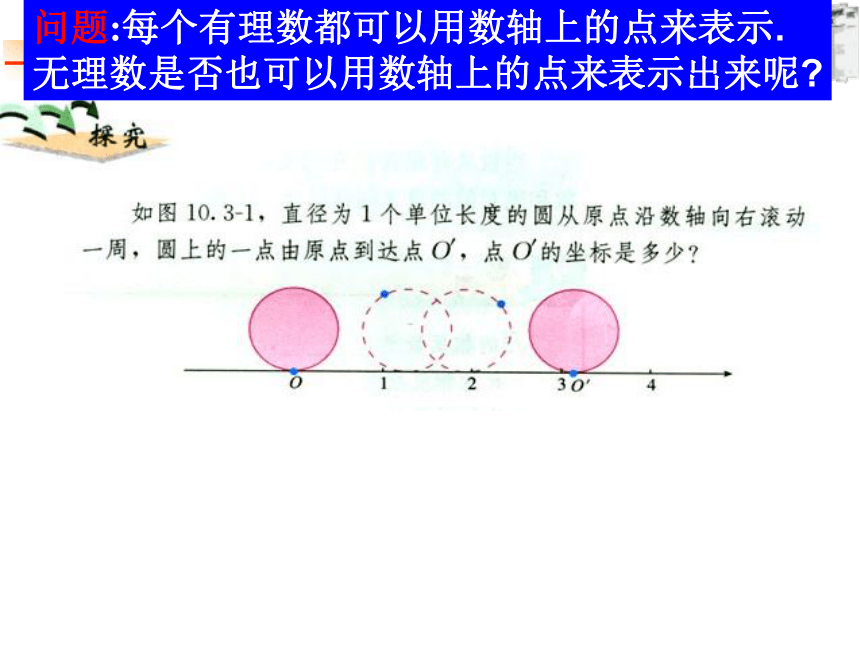
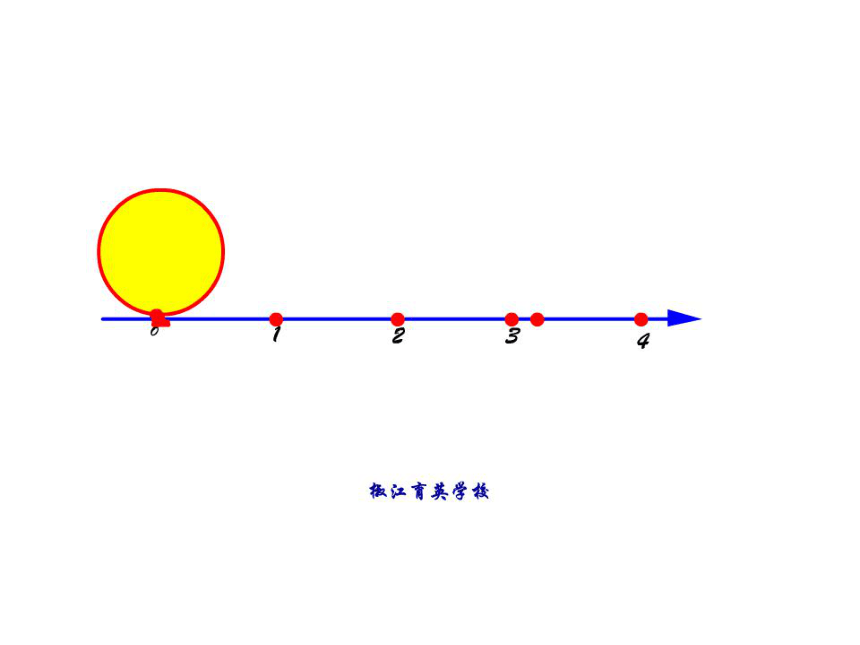
问题:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢?OO′的长是这个圆的周长 ,所以点O′的坐标是无理数 可以用数轴上的点来表示出来(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数,右边的数总比左边的数大。数轴上的点有些
表示有理数,有
些表示无理数.例1 比较下列各组数里两个数的大小随堂练习:P178解:点A表示-1.5; 点B表示 ;点C表示 ;点D表示3;点E表示 .深入探究:平面直角坐标系中的点与有序实数对之间 也存在一一对应关系吗?问:1、数从有理数扩充到实数后,我们经学过哪些运算?除法运算中除数不能为0;正数及0可以进行开平方运算任何实数都可以开立方运算有哪些规定?2、有理数满足哪些运算律?加法交换律:a+b=b+a加法结合律(a+b)+c=a+(b+c)乘法交换律ab=ba乘法结合律(ab)c=a(bc)分配律a(b+c)=ab+ac实数范围内运算与运算律仍适用例1、计算下列各式的值:(2)| |解:(分配律)(加法结合律)练习.计算解:(2)| |P178例2、计算:≈2.236+3.142≈5.38≈1.732×1.414≈2.45解:≈ ×2.24×1.41≈1.6答:?OAB的面积约是1.6.S?OAB=解:由已知可得OB= ,?OAB的OB边上的高为 变题:如图,点B的坐标为( ,0), ?OAB
面积为 ,点A的坐标为(1, y )
求A点的纵坐标.?OAB的OB边上的高为|y|.
∵S?OAB=∴ × × | y | =∴| y |=∴y =±∵点A在第一象限∴A点的纵坐标是解: (1)围成的四边形ABCD是长方形.(2)由已知AB=5-2=3,AD=(3)A、B、C、D四点的坐标分别变为(2, )、(5, )、
( 5, 0)、( 2, 0)P179四边形ABCD的面积=AB×AD =通过这节课的学习,你有哪些收获?1、判断下列说法是否正确:1. 无限小数都是无理数。( )6.无理数都是无限不循环小数。( )2.无理数都是无限小数。( )3.带根号的数都是无理数。( )5.所有的实数都可以用数轴上的点表示,反过来,数轴上所有的点都表示实数。( )7.两个无理数之积不一定是无理数。( )8.两个无理数之和一定是无理数。 ( )×××P1784.所有的有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数。 ( )×P179解:将l=0.5m代入公式t=2 ,得t≈2×3.14×0.22t≈1.4 (s)答:小重物来回摆动一次所用的时间约1.4s。P184解:将h=1.5代入公式s2=16.88h,得s2=25.32,≈5.03(km)将h=35代入公式s2=16.88h,得s2=590.8,≈24.31.03(km)解: 设圆的半径为r cm,正方形的边长为a cm.由题意,得 r2=2 , a2=2 ∴圆的周长C1=2 r =2 ∴C1
