2022-2023学年高一上学期数学人教A版(2019)必修第一册二次函数在闭区间上的最值 专题课件(共26张PPT)
文档属性
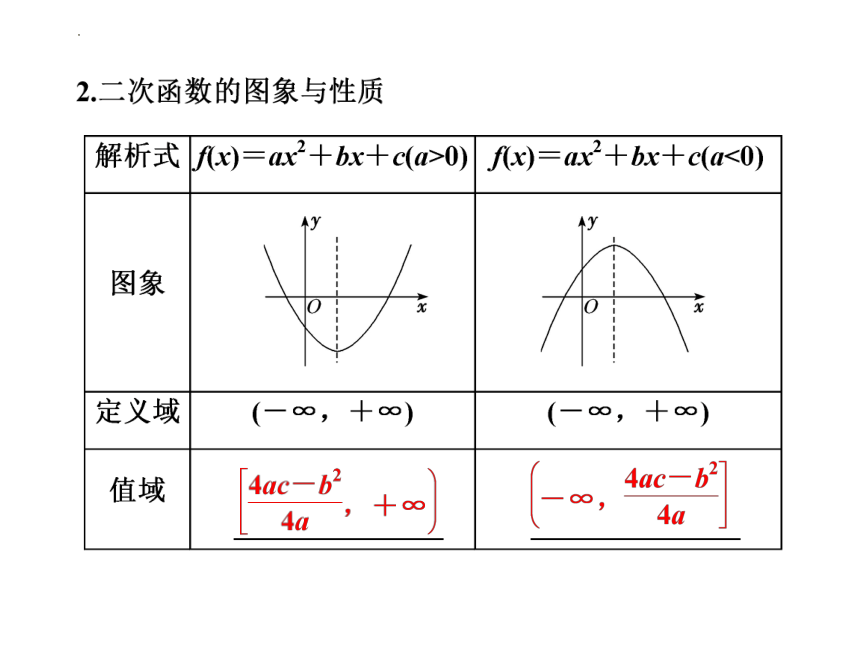
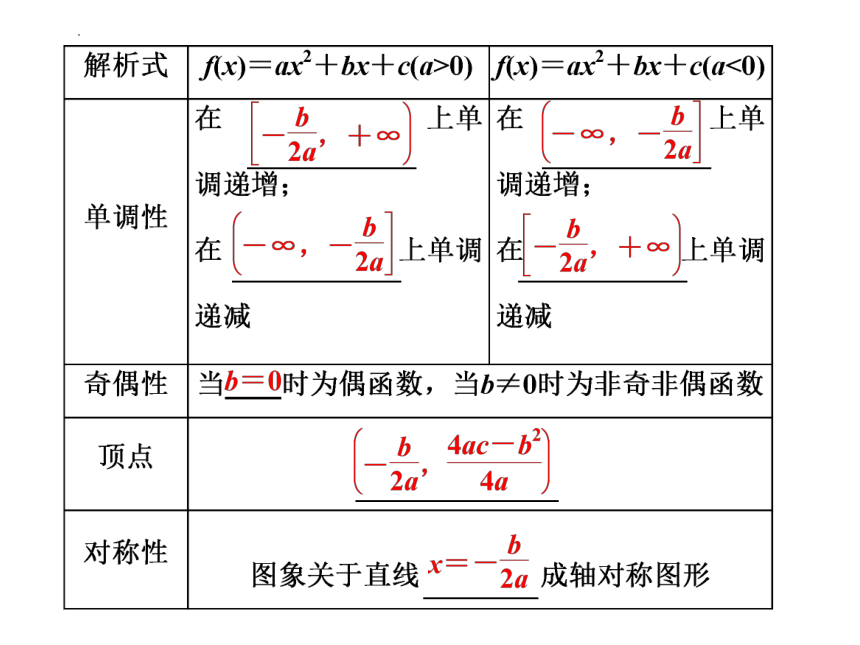
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册二次函数在闭区间上的最值 专题课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1015.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
二次函数在闭区间上的最值
上节课我们学习了定义域为实数的函数的最
值问题。如果我们遇到指定闭区间上的函数求最值或值域应该如何来做,这节课我们来研究二次函数的这个问题。
情境诱导,探求新知
复习导入,探求新知
例1、已知函数 在下列区间上的最值
(1) ∈[–2,0];
(2) ∈[ 2,4];
(3) ∈[ ];
(4) ∈[t,t+2],求函数f(x)的最小值.
例1、已知函数f(x)= x2–2x –3.
(1)若x∈[ –2,0 ], 求函数f(x)的最值;
1
0
x
y
–2
3
f(x)=x2 -2x-3
=(x-1)2 -4
解:
∵ -2≤x≤0
∴ 函数f(x)在 [ –2,0 ]上
是减函数。
∴ 当x= 0时, f(x)有最小值–3;
当x= –2时,f(x)有最大值5.
二、探求新知,三会表演
例1、已知函数f(x)= x2 –2x – 3.
1
0
x
y
2
3
4
– 1
(2)若x∈[ 2,4 ],求函数f(x)的最值;
∵ 2≤x≤4
∴ 函数f(x)在 [ 2,4 ]上是增函数。
∴ 当x= 2时, f(x)有最小值–3;
当x= 4时, f(x)有最大值5.
学生观察并说出结果:
例1、已知函数f(x)= x2 – 2x – 3.
y
1
0
x
2
3
4
– 1
(3)若x∈[ ],求
函数f(x)的最值;
当x= 1时,f(x)有最小值–4;
当x= 时,f(x)有最大值 。
学生观察并说出结果:
1
0
x
y
2
3
4
– 1
t
t +2
例1、已知函数 .
(4) ∈[t,t+2]时,
求函数f( )的最小值.
1
0
x
y
2
3
4
– 1
t
t +2
例1、已知函数 .
(4)x∈[t,t+2]时,求函数f(x)的最小值.
解:
f(x)=x2 -2x-3 = (x-1)2 -4
(2)当 t+2>1且t<1,即 -1<t<1 时
对称轴在区间内,
∴ 当 x=1时,f(x)取得最小值f(1)=-4.
.
(4)若x∈[t,t+2]时,求函数f(x)的最小值.
(1)当 t+2≤1,即 t≤ -1时
函数f(x)在【t,t+2】上为减函数,
∴ 当 x=t+2 时,f(x)取得最小值f(t+2)= t2+2t-3.
(3)当 t≥1时,函数f(x)在【t,t+2】上为增函数
∴ 当 x=t 时, f(x)取得最小值f(t)=t2-2t-3.
综上所述:
当t≤ -1时,函数的最小值为f(t+2)= t2+2t-3.
当-1<t<1时,函数的最小值为f(1)= -4.
当t ≥ 1时,函数的最小值为f(t)=t2+2t-3.
变式:(2)若函数f(x)=ax2+2ax+1在区间[1,2]上有最大值4,则a的值为________.
【解析】 (2)f(x)=a(x+1)2+1-a.
①当a=0时,函数f(x)在区间[1,2]上的值为常数1,不符合题意,舍去;
②当a>0时,函数f(x)在区间[1,2]上单调递增,最大值为f(2)=8a+1=4,解得a= ;
③当a<0时,函数f(x)在区间[1,2]上单调递减,最大值为f(1)=3a+1=4,解得a=1,不符合题意,舍去.
综上可知,a的值为 .
探 求 新 知 深 度 学 习
探 求 新 知 深 度 学 习
探 求 新 知 深 度 学 习
方法小结
方法小结
备选例题.例4.若函数f(x)=x|x-a|
在[0,2]上的最大值为2,则a的取值可以为( )
解析:当a≤0 ,f(x)在[0,2]上单调递增,
f(x)max=f(2)=2|2-a|=2,解得a=1(舍去)或a=3(舍去).
二次函数在闭区间上的最值
上节课我们学习了定义域为实数的函数的最
值问题。如果我们遇到指定闭区间上的函数求最值或值域应该如何来做,这节课我们来研究二次函数的这个问题。
情境诱导,探求新知
复习导入,探求新知
例1、已知函数 在下列区间上的最值
(1) ∈[–2,0];
(2) ∈[ 2,4];
(3) ∈[ ];
(4) ∈[t,t+2],求函数f(x)的最小值.
例1、已知函数f(x)= x2–2x –3.
(1)若x∈[ –2,0 ], 求函数f(x)的最值;
1
0
x
y
–2
3
f(x)=x2 -2x-3
=(x-1)2 -4
解:
∵ -2≤x≤0
∴ 函数f(x)在 [ –2,0 ]上
是减函数。
∴ 当x= 0时, f(x)有最小值–3;
当x= –2时,f(x)有最大值5.
二、探求新知,三会表演
例1、已知函数f(x)= x2 –2x – 3.
1
0
x
y
2
3
4
– 1
(2)若x∈[ 2,4 ],求函数f(x)的最值;
∵ 2≤x≤4
∴ 函数f(x)在 [ 2,4 ]上是增函数。
∴ 当x= 2时, f(x)有最小值–3;
当x= 4时, f(x)有最大值5.
学生观察并说出结果:
例1、已知函数f(x)= x2 – 2x – 3.
y
1
0
x
2
3
4
– 1
(3)若x∈[ ],求
函数f(x)的最值;
当x= 1时,f(x)有最小值–4;
当x= 时,f(x)有最大值 。
学生观察并说出结果:
1
0
x
y
2
3
4
– 1
t
t +2
例1、已知函数 .
(4) ∈[t,t+2]时,
求函数f( )的最小值.
1
0
x
y
2
3
4
– 1
t
t +2
例1、已知函数 .
(4)x∈[t,t+2]时,求函数f(x)的最小值.
解:
f(x)=x2 -2x-3 = (x-1)2 -4
(2)当 t+2>1且t<1,即 -1<t<1 时
对称轴在区间内,
∴ 当 x=1时,f(x)取得最小值f(1)=-4.
.
(4)若x∈[t,t+2]时,求函数f(x)的最小值.
(1)当 t+2≤1,即 t≤ -1时
函数f(x)在【t,t+2】上为减函数,
∴ 当 x=t+2 时,f(x)取得最小值f(t+2)= t2+2t-3.
(3)当 t≥1时,函数f(x)在【t,t+2】上为增函数
∴ 当 x=t 时, f(x)取得最小值f(t)=t2-2t-3.
综上所述:
当t≤ -1时,函数的最小值为f(t+2)= t2+2t-3.
当-1<t<1时,函数的最小值为f(1)= -4.
当t ≥ 1时,函数的最小值为f(t)=t2+2t-3.
变式:(2)若函数f(x)=ax2+2ax+1在区间[1,2]上有最大值4,则a的值为________.
【解析】 (2)f(x)=a(x+1)2+1-a.
①当a=0时,函数f(x)在区间[1,2]上的值为常数1,不符合题意,舍去;
②当a>0时,函数f(x)在区间[1,2]上单调递增,最大值为f(2)=8a+1=4,解得a= ;
③当a<0时,函数f(x)在区间[1,2]上单调递减,最大值为f(1)=3a+1=4,解得a=1,不符合题意,舍去.
综上可知,a的值为 .
探 求 新 知 深 度 学 习
探 求 新 知 深 度 学 习
探 求 新 知 深 度 学 习
方法小结
方法小结
备选例题.例4.若函数f(x)=x|x-a|
在[0,2]上的最大值为2,则a的取值可以为( )
解析:当a≤0 ,f(x)在[0,2]上单调递增,
f(x)max=f(2)=2|2-a|=2,解得a=1(舍去)或a=3(舍去).
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
