2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系2 课件(17张PPT))
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系2 课件(17张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览






文档简介
2.5.1 直线与圆的位置关系2
第二章 直线和圆的方程
例1.如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度????????=????????m,拱高????????=????m建造时每间隔4m需要用一根支柱支撑,求支柱????????????????的高度(精确到0.01 m).
?
A
B
A1
A2
A3
A4
O
P
P2
直线与圆位置关系的实际应用
解:建立如图所示的坐标系,设圆心坐标是(0,????),圆的半径是???? ,
则圆的方程是????2+(?????????)2=????2?.
?
答:支柱????2????2的长度约为3.86 m.
?
第一步:建立坐标系,用坐标和方程表示有关的量.
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系.
因为????>0,所以????=14.52?(?2)2?10.5≈14.36?10.5=3.86(m).
?
把点????2的横坐标????=?2?代入圆的方程,得?22+????+10.52=14.52.
?
把????(0,4)?????(10,0)代入圆的方程得方程组02+4?????2=????2,102+0?????2=????2,
?
解得????=??10.5,????2=14.52,
?
所以圆的方程是?????2+????+10.52=14.52
?
直线与圆位置关系的实际应用
归纳总结
坐标法解决平面几何问题的“三步曲”:
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
直线与圆位置关系的实际应用
练1.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
轮船
港口
台风
思考1:解决这个问题的本质是什么?
思考2:你有什么办法判断轮船航线是否经过台风圆域?
直线与圆位置关系的实际应用
例2.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?
轮船
港口
台风
x
y
o
直线与圆位置关系的实际应用
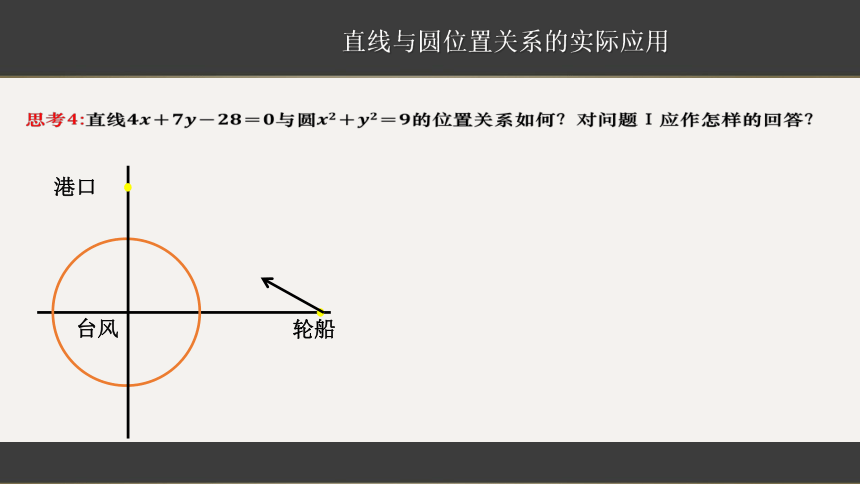
思考4:直线????????+????????-????????=????与圆????????+????????=????的位置关系如何?对问题Ⅰ应作怎样的回答?
?
轮船
港口
台风
直线与圆相切问题
(2)过圆上一点与圆相切的切线方程求法:
例2.过圆????:?????????+????????=????????上一点????(????,?????),?且与圆????相切的切线方程为__________.
?
x+3y-10=0
练2.过圆????:?(????-????)????+(????-????)????=????????上一点????(????,?????),?且与圆????相切的切线方程为_________.
?
3x-y=0
(1) 过圆外一点与圆相切的切线方程求法:
设?????????????=????(?????????????)
?
几何法代数法
?
直线与圆相切问题
归纳总结
一般地, 过圆C: x2+y2=r2上一点P(x0, y0), 且与圆C相切的切线方程为
一般地, 过圆C: (x-a)2+(y-b)2=r2上一点P(x0, y0), 且与圆C相切的切线方程为
直线与圆相切问题
变式:过圆外一点P(????????,????????)向圆?????2+????2=????2做切线,切于????、????两点,求过????、????的直线方程 .
?
·p
A
B
x
y
o
PA的方程为
PB的方程为
则有
可知A点在直线
B点在直线
所以AB的方程为
解:设
直线与圆相切问题
例3.已知从点P(m,3)向圆C:????????+????????+????????+????????+????=???? 引切线,求切线长的最小值.
?
练3.由直线????=????上的点向圆C:????????+?????????????????+????=???? 引切线,求切线长的最小值.
?
直线与圆相切问题
例4.若曲线????=????+????????????? 与直线????=????(?????????)+????有两个相异的交点,
求实数????的取值范围( )
?
变式:直线????=????+????
?
圆上点到直线的距离个数问题
例5. 圆C:????????+????????+????????+?????????????=????上到直线 ????+????+????=????的距离为?????的点共有几个?
?
练5. 设圆????????+?????????????????+????????+?????????????=????上有且仅有两个点到直线 ????????+?????????????????=????的距离为1,求????的取值范围.
?
变式. 若圆????????+???????????????????????????????????=????上至少有三个不同的点到直线 ????????+????????=????的距离为????????,求直线????斜率的取值范围.
?
圆上点到直线的距离个数问题
过直线与圆的交点的圆系方程
例6.求经过直线????+????=????与圆????????+????????+????????-????????-????=????的交点,且经过点????(-????,-????)的圆的方程.
?
法一:解方程组
所以直线与圆交于点A(1,-1)和点B(-4,4).
设所求圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
故所求圆的方程为x2+y2+3x-3y-8=0.
过直线与圆的交点的圆系方程
例6.求经过直线????+????=????与圆????????+????????+????????-????????-????=????的交点,且经过点????(-????,-????)的圆的方程.
?
方法二:设所求圆的方程为x2+y2+2x-4y-8+λ(x+y)=0,
又点P(-1,-2)在圆上,将(-1,-2)代入圆的方程得
(-1)2+(-2)2+2×(-1)-4×(-2)-8+λ(-1-2)=0,解得λ=1.
故所求圆的方程为x2+y2+2x-4y-8+x+y=0,
即x2+y2+3x-3y-8=0.
过直线与圆的交点的圆系方程
练6.已知圆????经过直线????+????+????=????与圆????????+????????=????的交点,且圆????的圆心在直线????????-????-????=????上,求圆????的方程.
?
课堂小结
代数方法
几何方法
图形直观判断
两图形方程判断
直线与圆的位置关系
相交 两个交点 d相切 一个交点 d=r
相离 没有交点 d>r
有无交点,有几个.
直线l与圆C的方程组成的方程组是否有解,有几个解.
判断圆C的圆心到直线l的距离d与圆的半径r的关系(大于、小于、等于).
判断直线与圆的位置关系
第二章 直线和圆的方程
例1.如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度????????=????????m,拱高????????=????m建造时每间隔4m需要用一根支柱支撑,求支柱????????????????的高度(精确到0.01 m).
?
A
B
A1
A2
A3
A4
O
P
P2
直线与圆位置关系的实际应用
解:建立如图所示的坐标系,设圆心坐标是(0,????),圆的半径是???? ,
则圆的方程是????2+(?????????)2=????2?.
?
答:支柱????2????2的长度约为3.86 m.
?
第一步:建立坐标系,用坐标和方程表示有关的量.
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系.
因为????>0,所以????=14.52?(?2)2?10.5≈14.36?10.5=3.86(m).
?
把点????2的横坐标????=?2?代入圆的方程,得?22+????+10.52=14.52.
?
把????(0,4)?????(10,0)代入圆的方程得方程组02+4?????2=????2,102+0?????2=????2,
?
解得????=??10.5,????2=14.52,
?
所以圆的方程是?????2+????+10.52=14.52
?
直线与圆位置关系的实际应用
归纳总结
坐标法解决平面几何问题的“三步曲”:
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
直线与圆位置关系的实际应用
练1.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
轮船
港口
台风
思考1:解决这个问题的本质是什么?
思考2:你有什么办法判断轮船航线是否经过台风圆域?
直线与圆位置关系的实际应用
例2.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?
轮船
港口
台风
x
y
o
直线与圆位置关系的实际应用
思考4:直线????????+????????-????????=????与圆????????+????????=????的位置关系如何?对问题Ⅰ应作怎样的回答?
?
轮船
港口
台风
直线与圆相切问题
(2)过圆上一点与圆相切的切线方程求法:
例2.过圆????:?????????+????????=????????上一点????(????,?????),?且与圆????相切的切线方程为__________.
?
x+3y-10=0
练2.过圆????:?(????-????)????+(????-????)????=????????上一点????(????,?????),?且与圆????相切的切线方程为_________.
?
3x-y=0
(1) 过圆外一点与圆相切的切线方程求法:
设?????????????=????(?????????????)
?
几何法代数法
?
直线与圆相切问题
归纳总结
一般地, 过圆C: x2+y2=r2上一点P(x0, y0), 且与圆C相切的切线方程为
一般地, 过圆C: (x-a)2+(y-b)2=r2上一点P(x0, y0), 且与圆C相切的切线方程为
直线与圆相切问题
变式:过圆外一点P(????????,????????)向圆?????2+????2=????2做切线,切于????、????两点,求过????、????的直线方程 .
?
·p
A
B
x
y
o
PA的方程为
PB的方程为
则有
可知A点在直线
B点在直线
所以AB的方程为
解:设
直线与圆相切问题
例3.已知从点P(m,3)向圆C:????????+????????+????????+????????+????=???? 引切线,求切线长的最小值.
?
练3.由直线????=????上的点向圆C:????????+?????????????????+????=???? 引切线,求切线长的最小值.
?
直线与圆相切问题
例4.若曲线????=????+????????????? 与直线????=????(?????????)+????有两个相异的交点,
求实数????的取值范围( )
?
变式:直线????=????+????
?
圆上点到直线的距离个数问题
例5. 圆C:????????+????????+????????+?????????????=????上到直线 ????+????+????=????的距离为?????的点共有几个?
?
练5. 设圆????????+?????????????????+????????+?????????????=????上有且仅有两个点到直线 ????????+?????????????????=????的距离为1,求????的取值范围.
?
变式. 若圆????????+???????????????????????????????????=????上至少有三个不同的点到直线 ????????+????????=????的距离为????????,求直线????斜率的取值范围.
?
圆上点到直线的距离个数问题
过直线与圆的交点的圆系方程
例6.求经过直线????+????=????与圆????????+????????+????????-????????-????=????的交点,且经过点????(-????,-????)的圆的方程.
?
法一:解方程组
所以直线与圆交于点A(1,-1)和点B(-4,4).
设所求圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
故所求圆的方程为x2+y2+3x-3y-8=0.
过直线与圆的交点的圆系方程
例6.求经过直线????+????=????与圆????????+????????+????????-????????-????=????的交点,且经过点????(-????,-????)的圆的方程.
?
方法二:设所求圆的方程为x2+y2+2x-4y-8+λ(x+y)=0,
又点P(-1,-2)在圆上,将(-1,-2)代入圆的方程得
(-1)2+(-2)2+2×(-1)-4×(-2)-8+λ(-1-2)=0,解得λ=1.
故所求圆的方程为x2+y2+2x-4y-8+x+y=0,
即x2+y2+3x-3y-8=0.
过直线与圆的交点的圆系方程
练6.已知圆????经过直线????+????+????=????与圆????????+????????=????的交点,且圆????的圆心在直线????????-????-????=????上,求圆????的方程.
?
课堂小结
代数方法
几何方法
图形直观判断
两图形方程判断
直线与圆的位置关系
相交 两个交点 d
相离 没有交点 d>r
有无交点,有几个.
直线l与圆C的方程组成的方程组是否有解,有几个解.
判断圆C的圆心到直线l的距离d与圆的半径r的关系(大于、小于、等于).
判断直线与圆的位置关系
