实数复习公开课[下学期]
文档属性
| 名称 | 实数复习公开课[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 407.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-31 00:00:00 | ||
图片预览








文档简介
课件29张PPT。实数复习本章主要内容有关概念特性:一个正数有两个平方根,它们互为相反数,零的平方根还是零。负数没有平方根。乘方互为逆运算开方平方根:一般地,如果一个数的平方等于a,这个数叫做a的平方根。(也叫二次方根)一 平方根与立方根开平方:求一个数的平方根的运算,叫做开平方。正数a的正的平方根也叫做a的算术平方根, 。
零的算术平方根还是零。
非负数a的算术平方根是非负数, 。 求一个数的立方根(三次方根)的运算,叫做开立方,开立方与立方互为逆运算。
一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。表示方法的取值性
质≥开
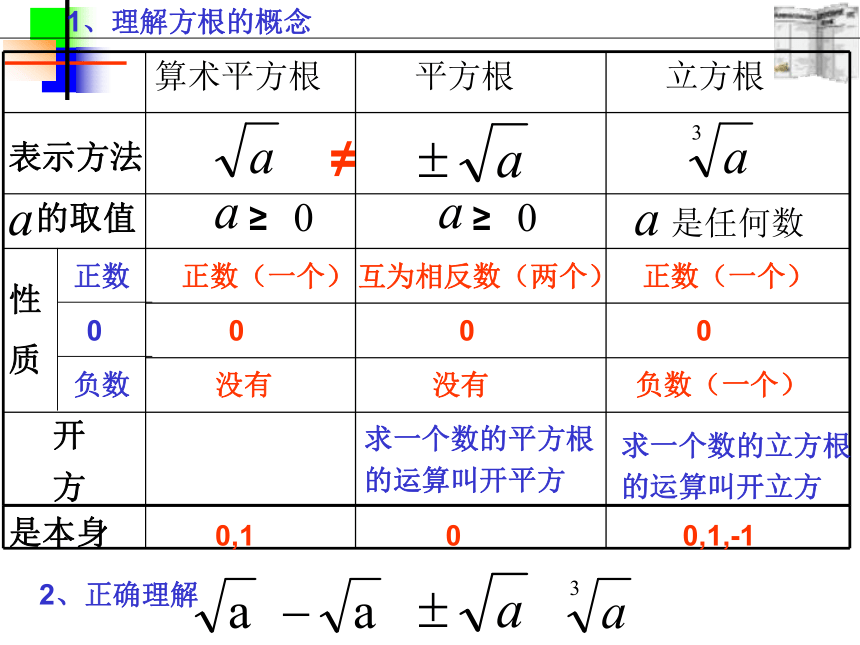
方≥正数0负数正数(一个)0没有互为相反数(两个)0没有正数(一个)0负数(一个)求一个数的平方根
的运算叫开平方求一个数的立方根
的运算叫开立方≠是本身0,100,1,-11、理解方根的概念2、正确理解常见错误:不要搞错了64±884(1)4的算术平方根是±2.(2)4的平方根是2.(3)8的立方是2.(4)无理数就是带根号的数.(5)不带根号的数都是有理数.(6)-1的立方根是-1
(7)-1的平方根是±1
判断题不要遗漏解下列方程:当方程中出现平方时,若有解,一般都有两个解解下列方程:当方程中出现立方时,一般都有一个解掌握规律=几个性质二 实数实数有理数无理数分数整数正无理数负无理数实数有理数无理数分数整数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况按符号分类从不同的角度观察问题例1、将下列各数分别填入下列的集合括号中自然数集合:整数集合:有理数集合:无理数集合:………是负数等于它的相反数是正数等于本身是负数里面的数的符号
化简绝对值要看它例2、必须掌握 在数轴上找出无理数在数轴上找出判断正误:
①-a一定是负数( )
②在实数中,如果一个数不是正数,则一定是负数( )
③开方开不尽的实数叫无理数( )
④无理数都是无限小数( )
⑤带根号的数是无理数( )
⑥没有最小的实数( )
⑦最小的整数是零( )
⑧任何实数的平方都是非负数( )相关练习 (1) 的倒数是 ;
(2) -2的绝对值是 ;
(3)若 ,且xy>0,x+y= 。 2 -3或- 3填空(4)计算三 计算器与实数的运算问题: 如图,神州六号的一块长方形零件,
长为 cm,宽为 cm。周长是_________________。那么这个长方形零件的面积是_________________。(结果保留3个有效数字)周长:∴面积:=6.29252874=6.29252874已知按一定规律排列的一组数,1,,,……, ,,如果从中选出若干个数使它们的和大于3,
那么至少要选出几个数? 探索题a、b为实数,且化简
零的算术平方根还是零。
非负数a的算术平方根是非负数, 。 求一个数的立方根(三次方根)的运算,叫做开立方,开立方与立方互为逆运算。
一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。表示方法的取值性
质≥开
方≥正数0负数正数(一个)0没有互为相反数(两个)0没有正数(一个)0负数(一个)求一个数的平方根
的运算叫开平方求一个数的立方根
的运算叫开立方≠是本身0,100,1,-11、理解方根的概念2、正确理解常见错误:不要搞错了64±884(1)4的算术平方根是±2.(2)4的平方根是2.(3)8的立方是2.(4)无理数就是带根号的数.(5)不带根号的数都是有理数.(6)-1的立方根是-1
(7)-1的平方根是±1
判断题不要遗漏解下列方程:当方程中出现平方时,若有解,一般都有两个解解下列方程:当方程中出现立方时,一般都有一个解掌握规律=几个性质二 实数实数有理数无理数分数整数正无理数负无理数实数有理数无理数分数整数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况按符号分类从不同的角度观察问题例1、将下列各数分别填入下列的集合括号中自然数集合:整数集合:有理数集合:无理数集合:………是负数等于它的相反数是正数等于本身是负数里面的数的符号
化简绝对值要看它例2、必须掌握 在数轴上找出无理数在数轴上找出判断正误:
①-a一定是负数( )
②在实数中,如果一个数不是正数,则一定是负数( )
③开方开不尽的实数叫无理数( )
④无理数都是无限小数( )
⑤带根号的数是无理数( )
⑥没有最小的实数( )
⑦最小的整数是零( )
⑧任何实数的平方都是非负数( )相关练习 (1) 的倒数是 ;
(2) -2的绝对值是 ;
(3)若 ,且xy>0,x+y= 。 2 -3或- 3填空(4)计算三 计算器与实数的运算问题: 如图,神州六号的一块长方形零件,
长为 cm,宽为 cm。周长是_________________。那么这个长方形零件的面积是_________________。(结果保留3个有效数字)周长:∴面积:=6.29252874=6.29252874已知按一定规律排列的一组数,1,,,……, ,,如果从中选出若干个数使它们的和大于3,
那么至少要选出几个数? 探索题a、b为实数,且化简
