1.2利用二分法求方程的近似解课件(共16张PPT)
文档属性
| 名称 | 1.2利用二分法求方程的近似解课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 975.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 15:16:12 | ||
图片预览






文档简介
(共16张PPT)
1.2 利用二分法求方程的近似解
核心知识目标 核心素养目标
1.通过具体实例理解二分法的概念及其使用条件.
2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解.
3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解. 1.通过对二分法概念的学
习,培养数学抽象素养.
2.通过利用二分法求函数零点的近似解,培养数学运算素养.
知识探究·素养培育
探究点一
[问题1] 现有外观相同的16枚金币,其中1枚较轻.现有一个无砝码的天平,请你设计能尽快找出这枚较轻金币的方案.
二分法
提示:把16枚金币一分为二,天平两端各放8枚,找出较轻的那一边,然后再把这8枚金币一分为二,天平两端各放4枚,找出较轻的那4枚,以此类推,直到剩余2枚时就可测出较轻的那枚金币.
知识点1:二分法的概念
(1)满足精度ε的近似解:设 是方程f(x)=0的一个解,给定正数ε,若x0满足 ,就称x0是满足精确度ε的近似解.
(2)二分法的定义:对于一般的函数y=f(x),x∈[a,b],若函数y=f(x)的图象是一条连续的曲线, ,则每次取区间的 ,将区间一分为二,再经比较,按需要留下其中一个小区间的求方程近似解的方法称为二分法.
|x0- |<ε
[思考1] 若函数y=f(x)在定义域内有零点,该零点是否一定能用二分法
求解
提示:二分法只适用于函数的变号零点(即函数在零点两侧符号相反),因此函数在零点两侧同号的零点不能用二分法求解,如f(x)=(x-1)2的零点就不能用二分法求解.
f(a)·f(b)<0
中点
[例1] 已知函数f(x)的图象如图所示,其中零点的个数与可以用二分法求解的个数分别为( )
(A)4,4 (B)3,4
(C)5,4 (D)4,3
解析:图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以可以用二分法求解的个数为3,故选D.
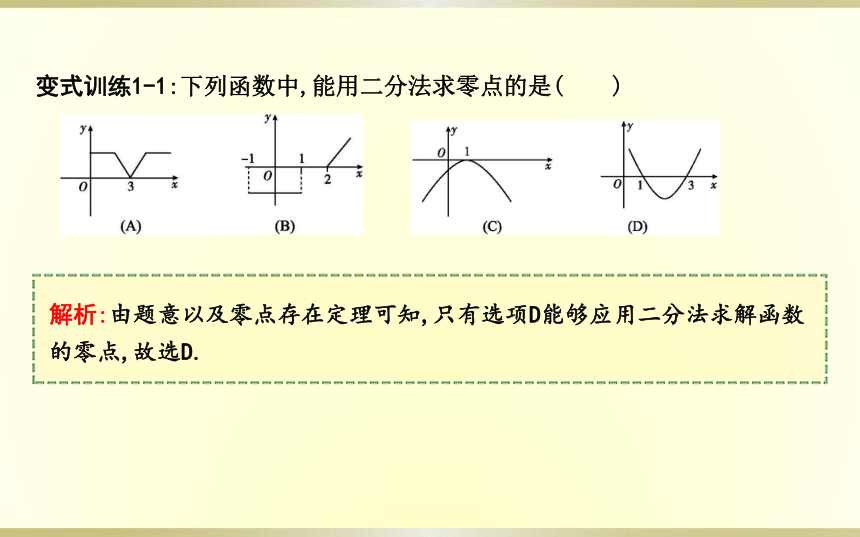
变式训练1-1:下列函数中,能用二分法求零点的是( )
解析:由题意以及零点存在定理可知,只有选项D能够应用二分法求解函数的零点,故选D.
方法总结
判断一个函数能否用二分法求其零点的依据是其图象在零点附近是连续不断的,且该零点为变号零点.因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用.
探究点二
二分法的步骤
[问题2] (1)函数f(x)=ln x+2x-6的零点所在的大致区间是( )
(A)(1,2) (B)(2,3)
(C)(3,4) (D)(4,5)
(2)如果利用二分法求函数f(x)=ln x+2x-6的近似零点,则接下来应该怎
么做
提示:(1)因为f(2)=ln 2-2<0,f(3)=ln 3>0,所以函数f(x)=ln x+2x-6的零点所在的大致区间为(2,3).
(2)如果利用二分法求函数的近似零点,接下来应该计算区间(2,3)中点的函数值f(2.5),然后再判定零点的大致区间,以此类推,直到达到要求的精确度为止.
知识点2:二分法求方程近似解的步骤
利用二分法求方程近似解的过程可以用下图表示出来.
异号
其中:“初始区间”是一个两端点函数值 的区间;
新区间的一个端点是原区间的 ,另一端点是原区间两端点中的一个,并且新区间两端点的函数值 .
中点
异号
[思考2] “精确到0.1”与“精确度为0.1”一样吗
提示:不一样.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后保留一位小数得1.3.而“精确度为0.1”指零点近似值所在区间(a,b)满足|a-b|<
0.1,比如零点近似值所在区间为(1.25,1.34).若精确度为0.1,则近似值可以是1.25,也可以是1.34.
[例2] 求方程x3-3=0的一个近似解.(精确度为0.02)
解:考查函数f(x)=x3-3,基于零点存在定理,从一个两端点函数值异号的区间开始,应用二分法逐步缩小方程解所在的区间.
经计算f(1)=-2<0,f(2)=5>0,
所以方程x3-3=0在区间(1,2)内有解.
取区间(1,2)的中点1.5,f(1.5)=0.375>0,
所以方程x3-3=0在区间(1,1.5)内有解.
如此下去,得到方程x3-3=0的解所在区间(如下表):
次数 左端点 左端点
函数值 右端点 右端点
函数值 区间长度
第1次 1 -2 2 5 1
第2次 1 -2 1.5 0.375 0.5
第3次 1.25 -1.047 1.5 0.375 0.25
第4次 1.375 -0.400 1.5 0.375 0.125
第5次 1.437 5 -0.030 1.5 0.375 0.062 5
第6次 1.437 5 -0.030 1.468 75 0.168 0.031 25
第7次 1.437 5 -0.030 1.453 125 0.068 4 0.015 625
至此可以看出区间[1.437 5,1.453 125]的区间长度小于0.02,而方程的近似解就在这个区间内,因此区间内任意一个数都是满足精确度的近似解,例如,1.45就是方程x3-3=0精确度为0.02的一个近似解.
变式训练2-1:根据下表,用二分法求函数f(x)=x3-3x+1在区间(1,2)上的零点的近似值(精确度为0.1)是 .
解析:由表中数据知f(1.5)·f(2)<0,f(1.5)·f(1.562 5)<0,所以函数零点在区间(1.5,1.562 5)上,又因为|1.562 5-1.5|=0.062 5<0.1,所以函数f(x)=x3-3x+1在区间(1,2)上的零点的近似值可以取1.5.
f(1)=-1 f(2)=3 f(1.5)=-0.125
f(1.75)=
1.109 375 f(1.625)=
0.416 015 625 f(1.562 5)=
0.127 197 265
答案:1.5
区间 中点的值 中点函数值
(1,2) 1.5 1.375
(1,1.5) 1.25 -0.046 9
(1.25,1.5) 1.375 0.599 6
(1.25,1.375) 1.312 5 0.261 0
(1.25,1.312 5) 1.281 25 0.103 3
(1.25,1.281 25) 1.265 625 0.027 3
(1.25,1.265 625) 1.257 812 5 -0.010 0
方法总结
(1)用二分法求方程近似解应遵循的原则
①需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法
完成).
②取区间端点的中点c,计算f(c),确定有解区间是(m,c)还是(c,n),逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.
(2)二分法求方程近似解步骤的记忆口诀
定区间,找中点,中值计算两边看.
同号丢,异号算,零点落在异号间.
周而复始怎么办 精确度上来判断.
1.2 利用二分法求方程的近似解
核心知识目标 核心素养目标
1.通过具体实例理解二分法的概念及其使用条件.
2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解.
3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解. 1.通过对二分法概念的学
习,培养数学抽象素养.
2.通过利用二分法求函数零点的近似解,培养数学运算素养.
知识探究·素养培育
探究点一
[问题1] 现有外观相同的16枚金币,其中1枚较轻.现有一个无砝码的天平,请你设计能尽快找出这枚较轻金币的方案.
二分法
提示:把16枚金币一分为二,天平两端各放8枚,找出较轻的那一边,然后再把这8枚金币一分为二,天平两端各放4枚,找出较轻的那4枚,以此类推,直到剩余2枚时就可测出较轻的那枚金币.
知识点1:二分法的概念
(1)满足精度ε的近似解:设 是方程f(x)=0的一个解,给定正数ε,若x0满足 ,就称x0是满足精确度ε的近似解.
(2)二分法的定义:对于一般的函数y=f(x),x∈[a,b],若函数y=f(x)的图象是一条连续的曲线, ,则每次取区间的 ,将区间一分为二,再经比较,按需要留下其中一个小区间的求方程近似解的方法称为二分法.
|x0- |<ε
[思考1] 若函数y=f(x)在定义域内有零点,该零点是否一定能用二分法
求解
提示:二分法只适用于函数的变号零点(即函数在零点两侧符号相反),因此函数在零点两侧同号的零点不能用二分法求解,如f(x)=(x-1)2的零点就不能用二分法求解.
f(a)·f(b)<0
中点
[例1] 已知函数f(x)的图象如图所示,其中零点的个数与可以用二分法求解的个数分别为( )
(A)4,4 (B)3,4
(C)5,4 (D)4,3
解析:图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以可以用二分法求解的个数为3,故选D.
变式训练1-1:下列函数中,能用二分法求零点的是( )
解析:由题意以及零点存在定理可知,只有选项D能够应用二分法求解函数的零点,故选D.
方法总结
判断一个函数能否用二分法求其零点的依据是其图象在零点附近是连续不断的,且该零点为变号零点.因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用.
探究点二
二分法的步骤
[问题2] (1)函数f(x)=ln x+2x-6的零点所在的大致区间是( )
(A)(1,2) (B)(2,3)
(C)(3,4) (D)(4,5)
(2)如果利用二分法求函数f(x)=ln x+2x-6的近似零点,则接下来应该怎
么做
提示:(1)因为f(2)=ln 2-2<0,f(3)=ln 3>0,所以函数f(x)=ln x+2x-6的零点所在的大致区间为(2,3).
(2)如果利用二分法求函数的近似零点,接下来应该计算区间(2,3)中点的函数值f(2.5),然后再判定零点的大致区间,以此类推,直到达到要求的精确度为止.
知识点2:二分法求方程近似解的步骤
利用二分法求方程近似解的过程可以用下图表示出来.
异号
其中:“初始区间”是一个两端点函数值 的区间;
新区间的一个端点是原区间的 ,另一端点是原区间两端点中的一个,并且新区间两端点的函数值 .
中点
异号
[思考2] “精确到0.1”与“精确度为0.1”一样吗
提示:不一样.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后保留一位小数得1.3.而“精确度为0.1”指零点近似值所在区间(a,b)满足|a-b|<
0.1,比如零点近似值所在区间为(1.25,1.34).若精确度为0.1,则近似值可以是1.25,也可以是1.34.
[例2] 求方程x3-3=0的一个近似解.(精确度为0.02)
解:考查函数f(x)=x3-3,基于零点存在定理,从一个两端点函数值异号的区间开始,应用二分法逐步缩小方程解所在的区间.
经计算f(1)=-2<0,f(2)=5>0,
所以方程x3-3=0在区间(1,2)内有解.
取区间(1,2)的中点1.5,f(1.5)=0.375>0,
所以方程x3-3=0在区间(1,1.5)内有解.
如此下去,得到方程x3-3=0的解所在区间(如下表):
次数 左端点 左端点
函数值 右端点 右端点
函数值 区间长度
第1次 1 -2 2 5 1
第2次 1 -2 1.5 0.375 0.5
第3次 1.25 -1.047 1.5 0.375 0.25
第4次 1.375 -0.400 1.5 0.375 0.125
第5次 1.437 5 -0.030 1.5 0.375 0.062 5
第6次 1.437 5 -0.030 1.468 75 0.168 0.031 25
第7次 1.437 5 -0.030 1.453 125 0.068 4 0.015 625
至此可以看出区间[1.437 5,1.453 125]的区间长度小于0.02,而方程的近似解就在这个区间内,因此区间内任意一个数都是满足精确度的近似解,例如,1.45就是方程x3-3=0精确度为0.02的一个近似解.
变式训练2-1:根据下表,用二分法求函数f(x)=x3-3x+1在区间(1,2)上的零点的近似值(精确度为0.1)是 .
解析:由表中数据知f(1.5)·f(2)<0,f(1.5)·f(1.562 5)<0,所以函数零点在区间(1.5,1.562 5)上,又因为|1.562 5-1.5|=0.062 5<0.1,所以函数f(x)=x3-3x+1在区间(1,2)上的零点的近似值可以取1.5.
f(1)=-1 f(2)=3 f(1.5)=-0.125
f(1.75)=
1.109 375 f(1.625)=
0.416 015 625 f(1.562 5)=
0.127 197 265
答案:1.5
区间 中点的值 中点函数值
(1,2) 1.5 1.375
(1,1.5) 1.25 -0.046 9
(1.25,1.5) 1.375 0.599 6
(1.25,1.375) 1.312 5 0.261 0
(1.25,1.312 5) 1.281 25 0.103 3
(1.25,1.281 25) 1.265 625 0.027 3
(1.25,1.265 625) 1.257 812 5 -0.010 0
方法总结
(1)用二分法求方程近似解应遵循的原则
①需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法
完成).
②取区间端点的中点c,计算f(c),确定有解区间是(m,c)还是(c,n),逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.
(2)二分法求方程近似解步骤的记忆口诀
定区间,找中点,中值计算两边看.
同号丢,异号算,零点落在异号间.
周而复始怎么办 精确度上来判断.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
