3.1从频数到频率3.2频率分布直方图课件(共22张PPT)
文档属性
| 名称 | 3.1从频数到频率3.2频率分布直方图课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 15:18:43 | ||
图片预览







文档简介
(共22张PPT)
§3 用样本估计总体分布
3.1 从频数到频率
3.2 频率分布直方图
核心知识目标 核心素养目标
1.了解频数与频率的关系,能合理利用频数和频率估计总体分布.
2.会列频率分布表、画频率分布直方图和折线图,会用样本频率分布直方图估计总体分布.
3.能综合利用各种统计表和统计图解答有关实际问题. 1.通过画频率分布直方图的过程,培养学生耐心细致、严谨认真的科学态度.
2.经历用统计的方法解决实际问题的过程,培养数学运算、数据分析
素养.
知识探究·素养培育
探究点一
从频数到频率
[问题1] 某次数学考试中,数学老师统计了他所教的两个班级的成绩,一班有5个同学不及格,二班的不及格率为10%.根据这些数据,你能判断哪一个班考得更好吗
提示:不能判断,因为我们不知道一班的总人数.若是一班总人数为50,那么不及格率也是10%,两班成绩一样;如果一班人数多于50,则一班成绩好一些;如果一班人数少于50,则一班成绩差一些.
知识点1:从频数到频率
频率反映了相对总数而言的相对强度,其所携带的总体信息远超过频数,在实际问题中,如果总体容量比较小, 也可以较客观地反映总体分布;当总体容量较大时, 就更能客观地反映总体分布.在统计中,经常要用 的频率去估计 中相应的频率,即对总体分布进行估计.
频数
频率
样本数据
总体
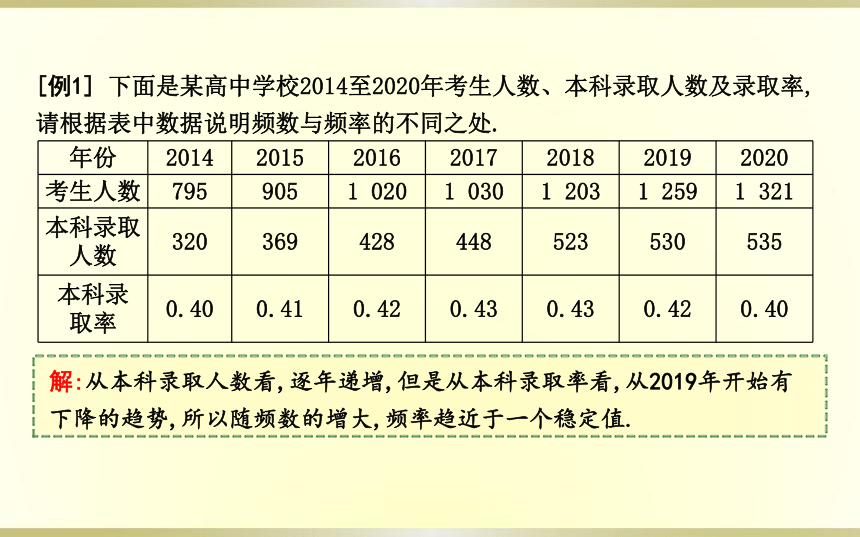
[例1] 下面是某高中学校2014至2020年考生人数、本科录取人数及录取率,请根据表中数据说明频数与频率的不同之处.
解:从本科录取人数看,逐年递增,但是从本科录取率看,从2019年开始有下降的趋势,所以随频数的增大,频率趋近于一个稳定值.
年份 2014 2015 2016 2017 2018 2019 2020
考生人数 795 905 1 020 1 030 1 203 1 259 1 321
本科录取人数 320 369 428 448 523 530 535
本科录
取率 0.40 0.41 0.42 0.43 0.43 0.42 0.40
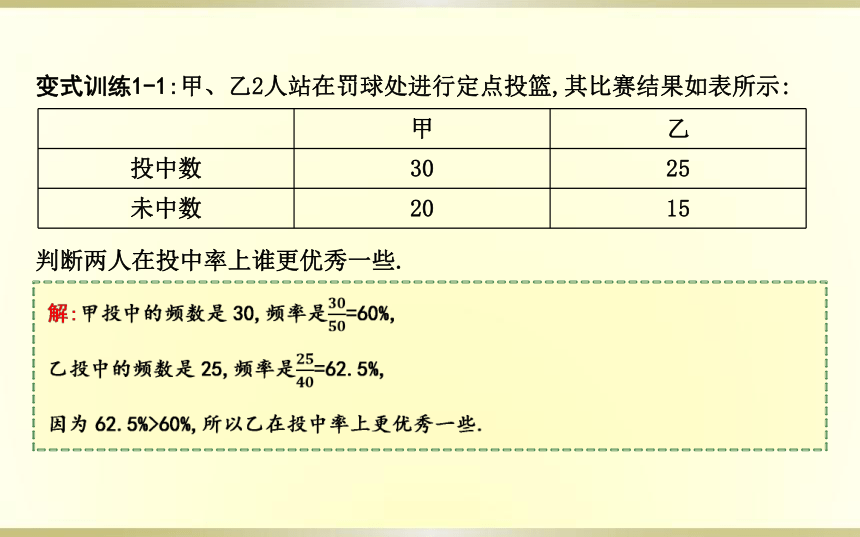
变式训练1-1:甲、乙2人站在罚球处进行定点投篮,其比赛结果如表所示:
判断两人在投中率上谁更优秀一些.
甲 乙
投中数 30 25
未中数 20 15
方法总结
当两个样本的样本容量相等或者相差不大的情况下,可以用频数比较总体分布的差异;当两个样本的样本容量相差较大的情况下,可以用频率比较总体分布的差异.
探究点二
频率分布直方图
[问题2] 为了直观反映样本数据分布情况,我们已经学习了一些常见的统计图的使用方法,请解答下面的问题.
(1)某中学甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A,B,C,D,E五个等级,绘制的统计图如图:
根据以上统计图提供的信息,则D等级这一组人数较多的班级是 .
提示:(1)由题意得甲班D等级的人数为13,乙班D等级的人数为40×30%=12<
13,所以D等级这一组人数较多的班级是甲班.
(2)某班全体学生某次测试成绩(单位:分)的统计图如下图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若不低于80分的人数是15,则该班的学生人数是 .
知识点2:频率分布直方图
[思考1] 频率分布直方图中,所有小矩形面积之和是多少
提示:频率分布直方图中,所有小矩形面积之和为1.
组距
频率与组距的比
频率
面积
[例2] 为了了解某中学的女生身体发育情况,对该中学的60名女生的身高进行了测量,结果如下(单位: cm):
167 154 159 166 169 159 156 166 162 158 159 156 166 160 164 160 157 156 157 161 158 158 153 158 164 158 163 158 163 157 162 162 159 154 165 166 157 151 146 151 158 160 163 158 163 163 162 161 154 165 162 162 159 157 159 149 164 168 159 153
画出频率分布直方图,并利用这个频率分布直方图估计该中学女生身高在[161.5,169.5]内的频率.
解:(1)计算极差:169-146=23(cm).
(3)分组:由于组距为4,6个组距的总长度超过极差,因此可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值,于是得到
[145.5,149.5),[149.5,153.5),…,[165.5,169.5].
(4)列频率分布表:
(5)画出频率分布直方图,如图所示.
变式训练2-1:为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示(单位:岁):
分组 频数 频率
[20,25) 5 0.05
[25,30) ① 0.20
[30,35) 35 ②
[35,40) 30 0.30
[40,45] 10 0.10
总计 100 1.00
(1)频率分布表中的①②位置应填什么数据
(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数.
方法总结
绘制频率分布直方图的步骤
(1)计算极差;
(2)确定组距与组数;
(3)分组;
(4)列表;
(5)画频率分布直方图.
探究点三
频率折线图
[问题3] 超速行驶是交通事故频发的主要原因之一.交警部门统计某日7:00~9:00经过某高速公路测速点的汽车的速度,得到如下折线图,若该路段汽车限速为110 km/h,则超速行驶的汽车有多少辆
提示:由图可知超过限速110 km/h的汽车有60+20=80(辆).
知识点3:在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间.从所加的左边区间的 开始,用线段依次连接各个矩形的 ,直至右边所加区间的中点,就可以得到一条折线,我们称之为频率折线图.
提示:在左边增加区间[141.5,145.5],在右边增加区间[169.5,173.5]
中点
顶端中点
[思考2] 我们现在要作出例2中的频率分布直方图对应的频率折线图,在原来分组的两边所加的区间(虚设区间)是什么
[例3] 作出由例2中的频率分布直方图得到的频率折线图,并写出频率折线图与横轴围成的封闭多边形的面积(不必说明理由).
解:在左边增加区间[141.5,145.5],在右边增加区间[169.5,173.5],并取这两个区间的中点,然后取原图中六个矩形的顶端中点,从左至右依次连接这8个点得到频率折线图,如图所示.
频率折线图与横轴围成的封闭多边形的面积是1.
方法总结
频率分布直方图和频率折线图能够直观地表明样本数据的分布情况,但是从频率分布直方图及频率折线图本身不能得出原始数据的内容,也就是说,把数据表示成频率分布直方图或频率折线图后,原有的具体数据信息就被抹掉了.解答有关用坐标系表示的统计图时,关键是理解横坐标和纵坐标的意义,据此转化为解题所需要的频率,最终都是利用频数与频率的关系求解.
§3 用样本估计总体分布
3.1 从频数到频率
3.2 频率分布直方图
核心知识目标 核心素养目标
1.了解频数与频率的关系,能合理利用频数和频率估计总体分布.
2.会列频率分布表、画频率分布直方图和折线图,会用样本频率分布直方图估计总体分布.
3.能综合利用各种统计表和统计图解答有关实际问题. 1.通过画频率分布直方图的过程,培养学生耐心细致、严谨认真的科学态度.
2.经历用统计的方法解决实际问题的过程,培养数学运算、数据分析
素养.
知识探究·素养培育
探究点一
从频数到频率
[问题1] 某次数学考试中,数学老师统计了他所教的两个班级的成绩,一班有5个同学不及格,二班的不及格率为10%.根据这些数据,你能判断哪一个班考得更好吗
提示:不能判断,因为我们不知道一班的总人数.若是一班总人数为50,那么不及格率也是10%,两班成绩一样;如果一班人数多于50,则一班成绩好一些;如果一班人数少于50,则一班成绩差一些.
知识点1:从频数到频率
频率反映了相对总数而言的相对强度,其所携带的总体信息远超过频数,在实际问题中,如果总体容量比较小, 也可以较客观地反映总体分布;当总体容量较大时, 就更能客观地反映总体分布.在统计中,经常要用 的频率去估计 中相应的频率,即对总体分布进行估计.
频数
频率
样本数据
总体
[例1] 下面是某高中学校2014至2020年考生人数、本科录取人数及录取率,请根据表中数据说明频数与频率的不同之处.
解:从本科录取人数看,逐年递增,但是从本科录取率看,从2019年开始有下降的趋势,所以随频数的增大,频率趋近于一个稳定值.
年份 2014 2015 2016 2017 2018 2019 2020
考生人数 795 905 1 020 1 030 1 203 1 259 1 321
本科录取人数 320 369 428 448 523 530 535
本科录
取率 0.40 0.41 0.42 0.43 0.43 0.42 0.40
变式训练1-1:甲、乙2人站在罚球处进行定点投篮,其比赛结果如表所示:
判断两人在投中率上谁更优秀一些.
甲 乙
投中数 30 25
未中数 20 15
方法总结
当两个样本的样本容量相等或者相差不大的情况下,可以用频数比较总体分布的差异;当两个样本的样本容量相差较大的情况下,可以用频率比较总体分布的差异.
探究点二
频率分布直方图
[问题2] 为了直观反映样本数据分布情况,我们已经学习了一些常见的统计图的使用方法,请解答下面的问题.
(1)某中学甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A,B,C,D,E五个等级,绘制的统计图如图:
根据以上统计图提供的信息,则D等级这一组人数较多的班级是 .
提示:(1)由题意得甲班D等级的人数为13,乙班D等级的人数为40×30%=12<
13,所以D等级这一组人数较多的班级是甲班.
(2)某班全体学生某次测试成绩(单位:分)的统计图如下图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若不低于80分的人数是15,则该班的学生人数是 .
知识点2:频率分布直方图
[思考1] 频率分布直方图中,所有小矩形面积之和是多少
提示:频率分布直方图中,所有小矩形面积之和为1.
组距
频率与组距的比
频率
面积
[例2] 为了了解某中学的女生身体发育情况,对该中学的60名女生的身高进行了测量,结果如下(单位: cm):
167 154 159 166 169 159 156 166 162 158 159 156 166 160 164 160 157 156 157 161 158 158 153 158 164 158 163 158 163 157 162 162 159 154 165 166 157 151 146 151 158 160 163 158 163 163 162 161 154 165 162 162 159 157 159 149 164 168 159 153
画出频率分布直方图,并利用这个频率分布直方图估计该中学女生身高在[161.5,169.5]内的频率.
解:(1)计算极差:169-146=23(cm).
(3)分组:由于组距为4,6个组距的总长度超过极差,因此可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值,于是得到
[145.5,149.5),[149.5,153.5),…,[165.5,169.5].
(4)列频率分布表:
(5)画出频率分布直方图,如图所示.
变式训练2-1:为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示(单位:岁):
分组 频数 频率
[20,25) 5 0.05
[25,30) ① 0.20
[30,35) 35 ②
[35,40) 30 0.30
[40,45] 10 0.10
总计 100 1.00
(1)频率分布表中的①②位置应填什么数据
(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数.
方法总结
绘制频率分布直方图的步骤
(1)计算极差;
(2)确定组距与组数;
(3)分组;
(4)列表;
(5)画频率分布直方图.
探究点三
频率折线图
[问题3] 超速行驶是交通事故频发的主要原因之一.交警部门统计某日7:00~9:00经过某高速公路测速点的汽车的速度,得到如下折线图,若该路段汽车限速为110 km/h,则超速行驶的汽车有多少辆
提示:由图可知超过限速110 km/h的汽车有60+20=80(辆).
知识点3:在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间.从所加的左边区间的 开始,用线段依次连接各个矩形的 ,直至右边所加区间的中点,就可以得到一条折线,我们称之为频率折线图.
提示:在左边增加区间[141.5,145.5],在右边增加区间[169.5,173.5]
中点
顶端中点
[思考2] 我们现在要作出例2中的频率分布直方图对应的频率折线图,在原来分组的两边所加的区间(虚设区间)是什么
[例3] 作出由例2中的频率分布直方图得到的频率折线图,并写出频率折线图与横轴围成的封闭多边形的面积(不必说明理由).
解:在左边增加区间[141.5,145.5],在右边增加区间[169.5,173.5],并取这两个区间的中点,然后取原图中六个矩形的顶端中点,从左至右依次连接这8个点得到频率折线图,如图所示.
频率折线图与横轴围成的封闭多边形的面积是1.
方法总结
频率分布直方图和频率折线图能够直观地表明样本数据的分布情况,但是从频率分布直方图及频率折线图本身不能得出原始数据的内容,也就是说,把数据表示成频率分布直方图或频率折线图后,原有的具体数据信息就被抹掉了.解答有关用坐标系表示的统计图时,关键是理解横坐标和纵坐标的意义,据此转化为解题所需要的频率,最终都是利用频数与频率的关系求解.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
