3频率与概率课件(共28张PPT)
文档属性
| 名称 | 3频率与概率课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:36:27 | ||
图片预览







文档简介
(共28张PPT)
§3 频率与概率
核心知识目标 核心素养目标
1.在具体情境中,了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.
2.会用概率的意义解释生活中的实例,通过做大量重复试验,用频率对某些随机事件的概率进行估计. 1.在正确理解随机事件发生的不确定性和频率的稳定性的基础上,能辨析生活中的随机现象,澄清生活中对概率的一些错误认识,培养数学抽象素养和逻辑思维素养.
2.通过对试验数据的运算和分析,培养数据分析素养和数学运算素养.
知识探究·素养培育
探究点一
用频率估计概率
知识点1:用频率估计概率
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,把这个常数叫作随机事件A的概率,记作P(A).显然, .我们通常用 来估计概率.
0≤P(A)≤1
频率
[思考1] 怎样理解频率与概率的关系
提示:频率与概率的区别与联系
名称 区别 联系
频率 本身是随机的,在试验之前无法确定,大多会随着试验次数的改变而改变.做同样次数的重复试验,得到的频率值也可能会不同 (1)频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率;
(2)在实际问题中,事件的概率通常情况下是未知的,常用频率估计概率
概率 是一个在[0,1]内的确定值,不随试验结果的改变而改变
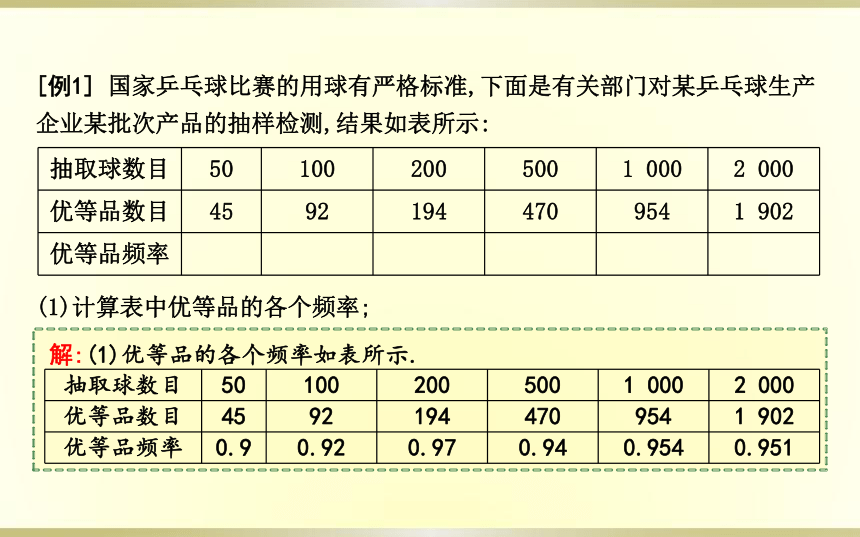
[例1] 国家乒乓球比赛的用球有严格标准,下面是有关部门对某乒乓球生产企业某批次产品的抽样检测,结果如表所示:
解:(1)优等品的各个频率如表所示.
抽取球数目 50 100 200 500 1 000 2 000
优等品数目 45 92 194 470 954 1 902
优等品频率
(1)计算表中优等品的各个频率;
抽取球数目 50 100 200 500 1 000 2 000
优等品数目 45 92 194 470 954 1 902
优等品频率 0.9 0.92 0.97 0.94 0.954 0.951
(2)从这批产品中任取一个乒乓球,质量检测为优等品的概率约是多少
解:(2)根据频率与概率的关系,可以认为从这批产品中任取一个乒乓球,质量检测为优等品的概率约是0.95.
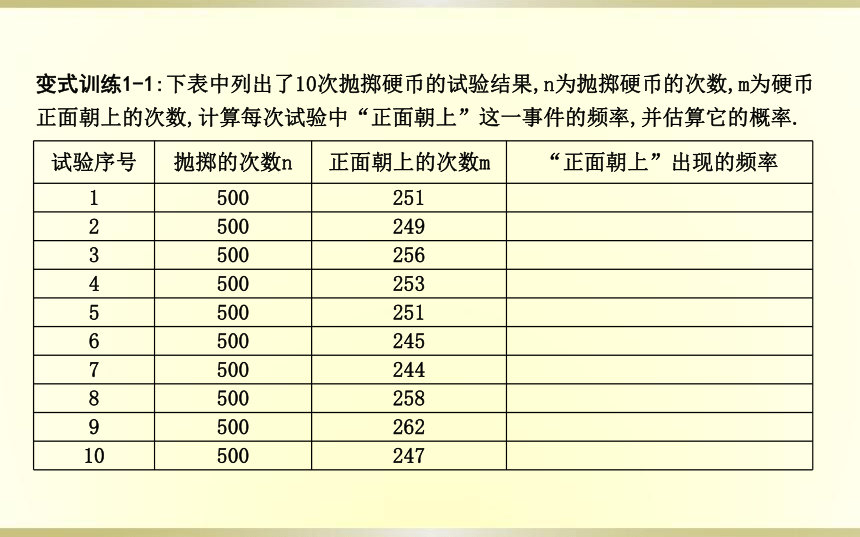
变式训练1-1:下表中列出了10次抛掷硬币的试验结果,n为抛掷硬币的次数,m为硬币正面朝上的次数,计算每次试验中“正面朝上”这一事件的频率,并估算它的概率.
试验序号 抛掷的次数n 正面朝上的次数m “正面朝上”出现的频率
1 500 251
2 500 249
3 500 256
4 500 253
5 500 251
6 500 245
7 500 244
8 500 258
9 500 262
10 500 247
方法总结
(1)频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率本身是随机变量,当n很大时,频率总是在一个稳定值附近摆动,这个稳定值就是概率.
(2)解此类题目的步骤:先利用频率的计算公式依次计算频率,然后用频率估计概率.
[问题2] 生活在湖边的渔民为了方便而快速地知道湖中有多少条鱼,常用一种称为“标记后再捕”的方法.先从湖中随意捕捉一定数量的鱼,例如1 000条鱼,在每条鱼的身上做记号后又放回湖中;隔了一段时间后,再从湖中捕捉一定数量的鱼,例如300条鱼,查看其中有多少条有标记的鱼,假设有20条有标记的鱼,估计湖中鱼的总数.
知识点2:用频率估计概率的试验设计
[思考2] 在用频率估计概率时,不同的试验结果对概率的估计值一样吗
频率
越大
提示:可能会得到不同的估计值.
[例2] (1)甲、乙两名同学进行乒乓球比赛,甲获胜的概率为0.4,现采用随机模拟的方法估计这两名同学打3局比赛甲恰好获胜2局的概率:先利用计算器产生0到9之间取整数值的随机数,制定用1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每3个随机数为一组,代表3局比赛的结果,经随机模拟产生了30组随机数:
102 231 146 027 590 763 245 207
310 386 350 481 337 286 139 579
684 487 370 175 772 235 246 487
569 047 008 341 287 114
据此估计,这两名同学打3局比赛甲恰好获胜2局的概率为( )
(2)天气预报显示,在今后的三天中,每一天下雨的概率为40%,现用随机模拟的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0~9之间取整数值的随机数,并制定用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
变式训练2-1:已知某运动员每次投篮命中的概率为80%.现采用随机模拟的方法估计该运动员三次投篮均命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中,再以每3个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮均命中的概率为( )
(A)0.40 (B)0.45 (C)0.50 (D)0.55
方法总结
事件A发生的概率为p,利用随机数设计n次重复试验中事件A发生k次的概率估计值的两个步骤
(1)根据概率p按比例规定事件A发生的频数与样本总数,事先规定哪些数字代表事件A发生,哪些数字代表A不发生.
(2)利用随机数表或者计算机产生随机数,n个数字为一组,找出所有数组中含有规定代表事件A发生的数组,用含有事件A发生的数字的数组个数除以数组总数即为n次重复试验中事件A发生k次的概率估计值.一般地,所利用的数组个数越多,估计值越接近于概率值.
拓展探索素养培优
[典例] 某高校对学生的思想品德、学业成绩、社会实践能力进行综合评
价,思想品德、学业成绩、社会实践能力评价指数分别记为x,y,z,每项评价指数都为1分,2分,3分,4分,5分五等,综合评价指标S=x+y+z,若S≥13,则该学生为优秀学生.现从该校学生中,随机抽取10名学生作为样本,分为A,B两组,其评价指数列表如下:
A组
学生编号 A1 A2 A3 A4 A5
评价指数
(x,y,z) (3,4,3) (4,3,4) (4,4,2) (4,3,5) (4,5,4)
B组
学生编号 B1 B2 B3 B4 B5
评价指数
(x,y,z) (3,5,3) (4,3,2) (5,4,4) (5,4,5) (4,5,3)
(1)从A,B两组中各选一名学生,依次记为甲、乙,求乙的综合评价指标大于甲的综合评价指标的概率;
(2)若该校共有1 500名学生,估计该校有多少名优秀学生.
试题情境:生活实践情境.
必备知识:用频率估计概率.
关键能力:逻辑思维能力.
学科素养:逻辑推理,数据分析.
备用例题
[例1] 某市正在全面普及数字电视,某住宅区有2万户住户,从中随机抽取200户,调查是否安装数字电视,调查的结果如下表所示,则估计该住宅区已安装数字电视的户数是( )
数字电视 老住户 新住户
已安装 30 50
未安装 65 55
(A)5 500 (B)5 000 (C)8 000 (D)9 500
[例2] 目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定人工种植的青蒿的长势等级:若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级.为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如表结果:
种植地
编号 A1 A2 A3 A4 A5
(x,y,z) (0,1,0) (1,2,1) (2,1,1) (2,2,2) (0,1,1)
种植地
编号 A6 A7 A8 A9 A10
(x,y,z) (1,1,2) (2,1,2) (2,0,1) (2,2,1) (0,2,1)
(1)若该地有青蒿人工种植地180个,试估计该人工种植地中长势等级为三级的个数;
(2)从长势等级为一级的青蒿人工种植地中随机抽取两个,求这两个人工种植地的综合指标ω均为4的概率.
§3 频率与概率
核心知识目标 核心素养目标
1.在具体情境中,了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.
2.会用概率的意义解释生活中的实例,通过做大量重复试验,用频率对某些随机事件的概率进行估计. 1.在正确理解随机事件发生的不确定性和频率的稳定性的基础上,能辨析生活中的随机现象,澄清生活中对概率的一些错误认识,培养数学抽象素养和逻辑思维素养.
2.通过对试验数据的运算和分析,培养数据分析素养和数学运算素养.
知识探究·素养培育
探究点一
用频率估计概率
知识点1:用频率估计概率
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,把这个常数叫作随机事件A的概率,记作P(A).显然, .我们通常用 来估计概率.
0≤P(A)≤1
频率
[思考1] 怎样理解频率与概率的关系
提示:频率与概率的区别与联系
名称 区别 联系
频率 本身是随机的,在试验之前无法确定,大多会随着试验次数的改变而改变.做同样次数的重复试验,得到的频率值也可能会不同 (1)频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率;
(2)在实际问题中,事件的概率通常情况下是未知的,常用频率估计概率
概率 是一个在[0,1]内的确定值,不随试验结果的改变而改变
[例1] 国家乒乓球比赛的用球有严格标准,下面是有关部门对某乒乓球生产企业某批次产品的抽样检测,结果如表所示:
解:(1)优等品的各个频率如表所示.
抽取球数目 50 100 200 500 1 000 2 000
优等品数目 45 92 194 470 954 1 902
优等品频率
(1)计算表中优等品的各个频率;
抽取球数目 50 100 200 500 1 000 2 000
优等品数目 45 92 194 470 954 1 902
优等品频率 0.9 0.92 0.97 0.94 0.954 0.951
(2)从这批产品中任取一个乒乓球,质量检测为优等品的概率约是多少
解:(2)根据频率与概率的关系,可以认为从这批产品中任取一个乒乓球,质量检测为优等品的概率约是0.95.
变式训练1-1:下表中列出了10次抛掷硬币的试验结果,n为抛掷硬币的次数,m为硬币正面朝上的次数,计算每次试验中“正面朝上”这一事件的频率,并估算它的概率.
试验序号 抛掷的次数n 正面朝上的次数m “正面朝上”出现的频率
1 500 251
2 500 249
3 500 256
4 500 253
5 500 251
6 500 245
7 500 244
8 500 258
9 500 262
10 500 247
方法总结
(1)频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率本身是随机变量,当n很大时,频率总是在一个稳定值附近摆动,这个稳定值就是概率.
(2)解此类题目的步骤:先利用频率的计算公式依次计算频率,然后用频率估计概率.
[问题2] 生活在湖边的渔民为了方便而快速地知道湖中有多少条鱼,常用一种称为“标记后再捕”的方法.先从湖中随意捕捉一定数量的鱼,例如1 000条鱼,在每条鱼的身上做记号后又放回湖中;隔了一段时间后,再从湖中捕捉一定数量的鱼,例如300条鱼,查看其中有多少条有标记的鱼,假设有20条有标记的鱼,估计湖中鱼的总数.
知识点2:用频率估计概率的试验设计
[思考2] 在用频率估计概率时,不同的试验结果对概率的估计值一样吗
频率
越大
提示:可能会得到不同的估计值.
[例2] (1)甲、乙两名同学进行乒乓球比赛,甲获胜的概率为0.4,现采用随机模拟的方法估计这两名同学打3局比赛甲恰好获胜2局的概率:先利用计算器产生0到9之间取整数值的随机数,制定用1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每3个随机数为一组,代表3局比赛的结果,经随机模拟产生了30组随机数:
102 231 146 027 590 763 245 207
310 386 350 481 337 286 139 579
684 487 370 175 772 235 246 487
569 047 008 341 287 114
据此估计,这两名同学打3局比赛甲恰好获胜2局的概率为( )
(2)天气预报显示,在今后的三天中,每一天下雨的概率为40%,现用随机模拟的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0~9之间取整数值的随机数,并制定用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
变式训练2-1:已知某运动员每次投篮命中的概率为80%.现采用随机模拟的方法估计该运动员三次投篮均命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中,再以每3个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮均命中的概率为( )
(A)0.40 (B)0.45 (C)0.50 (D)0.55
方法总结
事件A发生的概率为p,利用随机数设计n次重复试验中事件A发生k次的概率估计值的两个步骤
(1)根据概率p按比例规定事件A发生的频数与样本总数,事先规定哪些数字代表事件A发生,哪些数字代表A不发生.
(2)利用随机数表或者计算机产生随机数,n个数字为一组,找出所有数组中含有规定代表事件A发生的数组,用含有事件A发生的数字的数组个数除以数组总数即为n次重复试验中事件A发生k次的概率估计值.一般地,所利用的数组个数越多,估计值越接近于概率值.
拓展探索素养培优
[典例] 某高校对学生的思想品德、学业成绩、社会实践能力进行综合评
价,思想品德、学业成绩、社会实践能力评价指数分别记为x,y,z,每项评价指数都为1分,2分,3分,4分,5分五等,综合评价指标S=x+y+z,若S≥13,则该学生为优秀学生.现从该校学生中,随机抽取10名学生作为样本,分为A,B两组,其评价指数列表如下:
A组
学生编号 A1 A2 A3 A4 A5
评价指数
(x,y,z) (3,4,3) (4,3,4) (4,4,2) (4,3,5) (4,5,4)
B组
学生编号 B1 B2 B3 B4 B5
评价指数
(x,y,z) (3,5,3) (4,3,2) (5,4,4) (5,4,5) (4,5,3)
(1)从A,B两组中各选一名学生,依次记为甲、乙,求乙的综合评价指标大于甲的综合评价指标的概率;
(2)若该校共有1 500名学生,估计该校有多少名优秀学生.
试题情境:生活实践情境.
必备知识:用频率估计概率.
关键能力:逻辑思维能力.
学科素养:逻辑推理,数据分析.
备用例题
[例1] 某市正在全面普及数字电视,某住宅区有2万户住户,从中随机抽取200户,调查是否安装数字电视,调查的结果如下表所示,则估计该住宅区已安装数字电视的户数是( )
数字电视 老住户 新住户
已安装 30 50
未安装 65 55
(A)5 500 (B)5 000 (C)8 000 (D)9 500
[例2] 目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定人工种植的青蒿的长势等级:若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级.为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如表结果:
种植地
编号 A1 A2 A3 A4 A5
(x,y,z) (0,1,0) (1,2,1) (2,1,1) (2,2,2) (0,1,1)
种植地
编号 A6 A7 A8 A9 A10
(x,y,z) (1,1,2) (2,1,2) (2,0,1) (2,2,1) (0,2,1)
(1)若该地有青蒿人工种植地180个,试估计该人工种植地中长势等级为三级的个数;
(2)从长势等级为一级的青蒿人工种植地中随机抽取两个,求这两个人工种植地的综合指标ω均为4的概率.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
