第七章概率章末总结课件(共38张PPT)
文档属性
| 名称 | 第七章概率章末总结课件(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:39:05 | ||
图片预览










文档简介
(共38张PPT)
章末总结
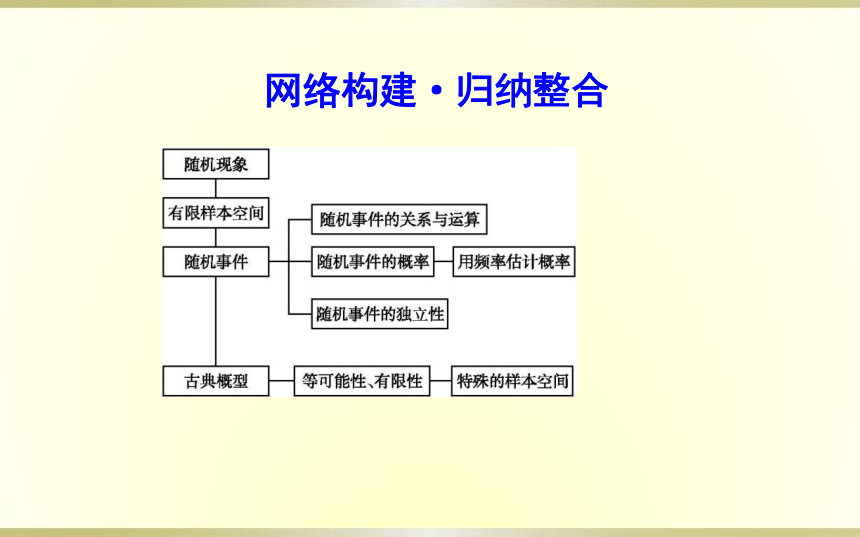
网络构建·归纳整合
题型归纳·素养提升
真题体验·素养落地
网络构建·归纳整合
题型归纳·素养提升
题型一 古典概型
[例1] 从标号分别为1,2,3,4,5的5张标签中随机抽取一张,放回后再随机抽取一张,则抽得的第一张标签的标号与第二张标签的标号恰好相差1的概率为( )
跟踪训练1-1:某学习小组有2个男生,3个女生,从该小组选取2人参加解题比赛,选到一男一女的概率为( )
规律总结
古典概型是一个非常重要的概率模型,高考中常常以小题的形式出现,主要考查列举法,为了避免遗漏或重复,有序的思考、合理的分类是解决问题的关键.
题型二 互斥与独立
(1)从甲、乙两人中选取1人参加比赛,派谁参赛赢得比赛的概率更大
(2)若甲、乙两人均参加比赛,求两人中至少有一人赢得比赛的概率.
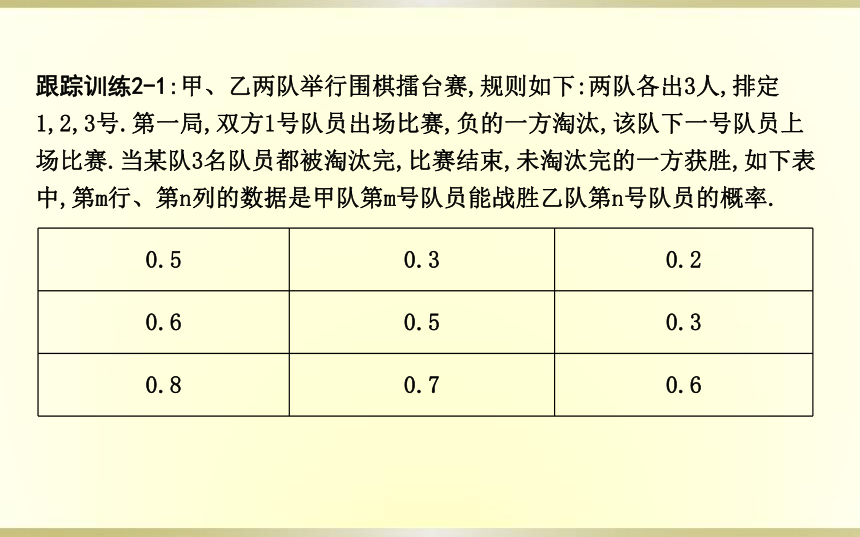
跟踪训练2-1:甲、乙两队举行围棋擂台赛,规则如下:两队各出3人,排定1,2,3号.第一局,双方1号队员出场比赛,负的一方淘汰,该队下一号队员上场比赛.当某队3名队员都被淘汰完,比赛结束,未淘汰完的一方获胜,如下表中,第m行、第n列的数据是甲队第m号队员能战胜乙队第n号队员的概率.
0.5 0.3 0.2
0.6 0.5 0.3
0.8 0.7 0.6
(1)求甲队2号队员把乙队3名队员都淘汰的概率;
解:(1)甲队2号队员把乙队3名队员都淘汰的概率为P=0.5×0.6×0.5×
0.3=0.045.
(2)比较第三局比赛,甲队队员和乙队队员哪个获胜的概率更大一些
解:(2)第三局比赛甲队队员获胜可分为3个互斥事件:
①甲队1号胜乙队3号,概率为0.5×0.3×0.2=0.03;
②甲队2号胜乙队2号,概率为0.5×0.7×0.5+0.5×0.6×0.5=0.325;
③甲队3号胜乙队1号,概率为0.5×0.4×0.8=0.16,
所以第三局甲队队员获胜的概率为P=0.03+0.325+0.16=0.515,
所以第三局乙队队员获胜的概率为1-0.515=0.485.
因为0.515>0.485,
所以甲队队员获胜的概率更大一些.
规律总结
题型三 频率与概率
[例3] 为了解学生“课外阅读日”的活动情况,某校以10%的比例对高二年级500名学生按选修物理和选修历史进行分层随机抽样调查,测得阅读时间(单位:分)的频数统计图如图:
(1)分别估计该校高二年级选修物理和选修历史的人数;
解:(1)因为以10%的比例对高二年级500名学生按选修物理和选修历史进行分层随机抽样,
所以估计该校高二年级选修物理的人数为(6+9+9+3+2+1)×10=300,
所以估计该校高二年级选修历史的人数为500-300=200.
(2)估计该校高二年级学生阅读时间在60分以上的概率;
(3)从样本中阅读时间在60~90分的选修物理的学生中任选2人,求至少有1人阅读时间在75~90分之间的概率.
跟踪训练3-1:疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品.现随机抽取100件口罩进行检测,其结果如表:
测试分数 [50,60) [60,70) [70,80) [80,90) [90,100]
数量 4 16 42 24 14
(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层随机抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
跟踪训练3-2:已知一工厂生产了某种产品700件,该工厂需要对这些产品的性能进行检测,现决定利用随机数法从中抽取100件产品进行抽样检测,将700件产品按001,
002,…,700进行编号.
(1)如果从随机数表的第8行第4列开始向右读,请你依次写出最先检测的3件产品的编号.(下面摘取了随机数表的第7~9行)
8442 1753 3157 2455 0688 7704 7447 6721 7633 5025 8392 1206 76(第7行)
6301 6378 5916 9555 6719 9810 5071 7512 8673 5807 4439 5238 79(第8行)
3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54(第9行)
解:(1)依题意,最先检测的三件产品的编号为163,567,199.
(2)检测结果分为优等、合格、不合格三个等级,抽取的100件产品的安全性能和环保性能的检测结果如下表(横向和纵向分别表示安全性能和环保性能).
①若在该样本中,产品环保性能是优等的概率为34%,求m,n的值;
②若m≥12,n≥8,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
件数 环保性能
优等 合格 不合格
安全
性能 优等 6 20 5
合格 10 18 6
不合格 m 4 n
规律总结
概率是一个稳定的数值,也就是某件事发生或不发生的可能性大小.频率是在一定数量的某件事情上,发生的次数与总数的比值.频率是有限次数的试验所得的结果,概率是频数无限大时对应的频率,是唯一确定的常数.尽管每进行一连串(n次)试验,所得到的频率可以各不相同,但只要n相当大,频率与概率会非常接近.
真题体验·素养落地
题型一 古典概型
1.(2020·全国Ⅰ卷T4)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A
2.(2018·全国Ⅱ卷T8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
C
3.(2020·江苏卷T4)将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 .
题型二 互斥与独立
5.(2020·全国Ⅰ卷)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
6.(2019·全国Ⅱ卷T18)11分制乒乓球比赛,每赢一球得1分,当某局打成10∶10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10∶10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
解:(1)X=2就是双方打成10∶10平后,两人又打了2个球该局比赛结束,则这2个球均由甲得分,或者均由乙得分.因此P(X=2)=0.5×0.4+(1-0.5)×
(1-0.4)=0.5.
(2)求事件“X=4且甲获胜”的概率.
解:(2)X=4且甲获胜,就是双方打成10∶10平后,两人又打了4个球该局比赛结束,且这4个球的得分情况为前两球是甲、乙各得1分,后两球均为甲得分.
因此所求概率为[0.5×(1-0.4)+(1-0.5)×0.4]×0.5×0.4=0.1.
题型三 频率与概率
7.(2020·全国Ⅰ卷T17)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元、50元、20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务
解:(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为
利润 65 25 -5 -75
频数 40 20 20 20
由数据知乙分厂加工出来的100件产品利润的频数分布表为
利润 70 30 0 -70
频数 28 17 34 21
章末总结
网络构建·归纳整合
题型归纳·素养提升
真题体验·素养落地
网络构建·归纳整合
题型归纳·素养提升
题型一 古典概型
[例1] 从标号分别为1,2,3,4,5的5张标签中随机抽取一张,放回后再随机抽取一张,则抽得的第一张标签的标号与第二张标签的标号恰好相差1的概率为( )
跟踪训练1-1:某学习小组有2个男生,3个女生,从该小组选取2人参加解题比赛,选到一男一女的概率为( )
规律总结
古典概型是一个非常重要的概率模型,高考中常常以小题的形式出现,主要考查列举法,为了避免遗漏或重复,有序的思考、合理的分类是解决问题的关键.
题型二 互斥与独立
(1)从甲、乙两人中选取1人参加比赛,派谁参赛赢得比赛的概率更大
(2)若甲、乙两人均参加比赛,求两人中至少有一人赢得比赛的概率.
跟踪训练2-1:甲、乙两队举行围棋擂台赛,规则如下:两队各出3人,排定1,2,3号.第一局,双方1号队员出场比赛,负的一方淘汰,该队下一号队员上场比赛.当某队3名队员都被淘汰完,比赛结束,未淘汰完的一方获胜,如下表中,第m行、第n列的数据是甲队第m号队员能战胜乙队第n号队员的概率.
0.5 0.3 0.2
0.6 0.5 0.3
0.8 0.7 0.6
(1)求甲队2号队员把乙队3名队员都淘汰的概率;
解:(1)甲队2号队员把乙队3名队员都淘汰的概率为P=0.5×0.6×0.5×
0.3=0.045.
(2)比较第三局比赛,甲队队员和乙队队员哪个获胜的概率更大一些
解:(2)第三局比赛甲队队员获胜可分为3个互斥事件:
①甲队1号胜乙队3号,概率为0.5×0.3×0.2=0.03;
②甲队2号胜乙队2号,概率为0.5×0.7×0.5+0.5×0.6×0.5=0.325;
③甲队3号胜乙队1号,概率为0.5×0.4×0.8=0.16,
所以第三局甲队队员获胜的概率为P=0.03+0.325+0.16=0.515,
所以第三局乙队队员获胜的概率为1-0.515=0.485.
因为0.515>0.485,
所以甲队队员获胜的概率更大一些.
规律总结
题型三 频率与概率
[例3] 为了解学生“课外阅读日”的活动情况,某校以10%的比例对高二年级500名学生按选修物理和选修历史进行分层随机抽样调查,测得阅读时间(单位:分)的频数统计图如图:
(1)分别估计该校高二年级选修物理和选修历史的人数;
解:(1)因为以10%的比例对高二年级500名学生按选修物理和选修历史进行分层随机抽样,
所以估计该校高二年级选修物理的人数为(6+9+9+3+2+1)×10=300,
所以估计该校高二年级选修历史的人数为500-300=200.
(2)估计该校高二年级学生阅读时间在60分以上的概率;
(3)从样本中阅读时间在60~90分的选修物理的学生中任选2人,求至少有1人阅读时间在75~90分之间的概率.
跟踪训练3-1:疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品.现随机抽取100件口罩进行检测,其结果如表:
测试分数 [50,60) [60,70) [70,80) [80,90) [90,100]
数量 4 16 42 24 14
(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层随机抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
跟踪训练3-2:已知一工厂生产了某种产品700件,该工厂需要对这些产品的性能进行检测,现决定利用随机数法从中抽取100件产品进行抽样检测,将700件产品按001,
002,…,700进行编号.
(1)如果从随机数表的第8行第4列开始向右读,请你依次写出最先检测的3件产品的编号.(下面摘取了随机数表的第7~9行)
8442 1753 3157 2455 0688 7704 7447 6721 7633 5025 8392 1206 76(第7行)
6301 6378 5916 9555 6719 9810 5071 7512 8673 5807 4439 5238 79(第8行)
3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54(第9行)
解:(1)依题意,最先检测的三件产品的编号为163,567,199.
(2)检测结果分为优等、合格、不合格三个等级,抽取的100件产品的安全性能和环保性能的检测结果如下表(横向和纵向分别表示安全性能和环保性能).
①若在该样本中,产品环保性能是优等的概率为34%,求m,n的值;
②若m≥12,n≥8,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
件数 环保性能
优等 合格 不合格
安全
性能 优等 6 20 5
合格 10 18 6
不合格 m 4 n
规律总结
概率是一个稳定的数值,也就是某件事发生或不发生的可能性大小.频率是在一定数量的某件事情上,发生的次数与总数的比值.频率是有限次数的试验所得的结果,概率是频数无限大时对应的频率,是唯一确定的常数.尽管每进行一连串(n次)试验,所得到的频率可以各不相同,但只要n相当大,频率与概率会非常接近.
真题体验·素养落地
题型一 古典概型
1.(2020·全国Ⅰ卷T4)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A
2.(2018·全国Ⅱ卷T8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
C
3.(2020·江苏卷T4)将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 .
题型二 互斥与独立
5.(2020·全国Ⅰ卷)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
6.(2019·全国Ⅱ卷T18)11分制乒乓球比赛,每赢一球得1分,当某局打成10∶10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10∶10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
解:(1)X=2就是双方打成10∶10平后,两人又打了2个球该局比赛结束,则这2个球均由甲得分,或者均由乙得分.因此P(X=2)=0.5×0.4+(1-0.5)×
(1-0.4)=0.5.
(2)求事件“X=4且甲获胜”的概率.
解:(2)X=4且甲获胜,就是双方打成10∶10平后,两人又打了4个球该局比赛结束,且这4个球的得分情况为前两球是甲、乙各得1分,后两球均为甲得分.
因此所求概率为[0.5×(1-0.4)+(1-0.5)×0.4]×0.5×0.4=0.1.
题型三 频率与概率
7.(2020·全国Ⅰ卷T17)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元、50元、20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务
解:(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为
利润 65 25 -5 -75
频数 40 20 20 20
由数据知乙分厂加工出来的100件产品利润的频数分布表为
利润 70 30 0 -70
频数 28 17 34 21
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
