8.1走近数学建模 8.2数学建模的主要步骤 8.3数学建模活动的主要过程 课件(共48张PPT)
文档属性
| 名称 | 8.1走近数学建模 8.2数学建模的主要步骤 8.3数学建模活动的主要过程 课件(共48张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 13:48:30 | ||
图片预览










文档简介
(共48张PPT)
第八章 数学建模活动(一)
§1 走近数学建模
§2 数学建模的主要步骤
§3 数学建模活动的主要过程
核心知识目标 核心素养目标
1.了解熟悉数学模型的实际背景及其数学描述,了解数学模型中的参数、结论的实际含义.
2.知道数学建模的一般步骤包括提出问题、建立模型、求解模型、检验结果.能够在熟悉的实际情境中,模仿学过的数学建模过程解决问题.
3.对于学过的数学模型,能够举例说明建模的意义,体会其蕴含的数学思想;感悟数学表达对数学建模的重要性.在交流的过程中,能够借助或引用已有数学建模的结果说明问题.
4.知道数学建模活动的主要过程包括选题、开题、做题、结题,能够选择简单的实际问题,完成数学建模活动. 1.通过在综合的情境中,运用数学思维进行分析,发现情境中的数学关系,提出数学问题,运用数学建模的一般方法和相关知识,建立数学模型,解决问题,培养数学建模素养.
2.通过理解数学建模的意义和作用,运用数学语言,清晰、准确地表达数学建模的过程和结果,在交流的过程中,能够通过数学建模的结论和思想阐释科学规律和社会现象,培养数学运算、逻辑推理和数据分析素养.
知识探究·素养培育
探究点一
走近数学建模
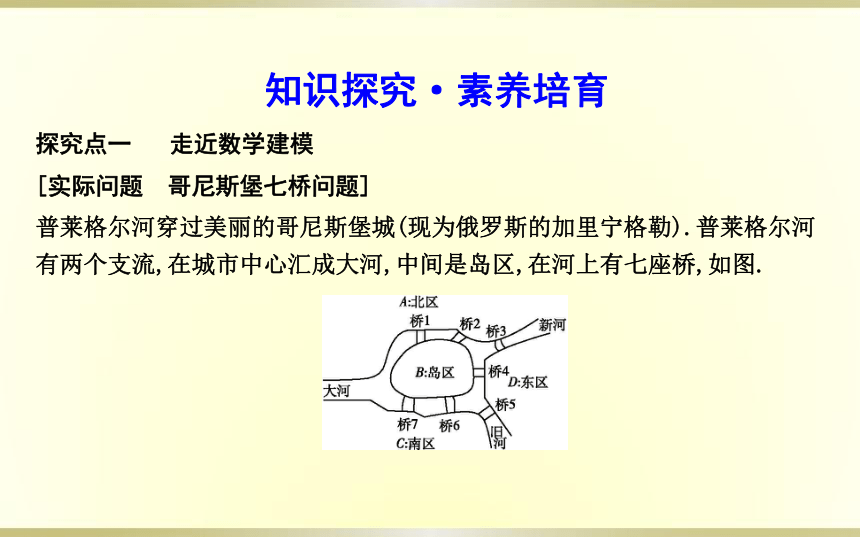
[实际问题 哥尼斯堡七桥问题]
普莱格尔河穿过美丽的哥尼斯堡城(现为俄罗斯的加里宁格勒).普莱格尔河有两个支流,在城市中心汇成大河,中间是岛区,在河上有七座桥,如图.
岛上有古老的哥尼斯堡大学、知名的大教堂,居民经常到河岸和桥上散步.在18世纪初的一天,有人突发奇想:如何才能走过这七座桥,而每座桥都只能经过一次,最后又回到原来的出发点 人们开始沉迷于这个问题,在桥上来来回回不知走了多少次,却始终不得其解.这就是著名的哥尼斯堡七桥问题.
[实际问题的数学表述]
七桥问题引起了数学家欧拉的极大兴趣.他想:经过这么多人的努力都没有找到一次不重复走完七座桥的路径,会不会根本不存在这样的走法
首先,欧拉想到的是列举法,就是把所有的走法都一一列出来,再一个一个验证.但是,他很快发现这样做太麻烦了,因为对七座桥的不同走法就有5 000多种,并且这种方法不具有通用性.
经过反复思考,欧拉想到:岛的形状、大小,以及桥的长短、宽窄并不影响结果,重要的是陆地、桥与岛这三者之间的位置关系.不妨把图中被河隔开的4块陆地看作4个点,连接陆地的7座桥看作7条线,就得到如图的图形.实际问题中的陆地、河流和桥梁景观就不见了,七桥问题就变成能否一笔画出此图形的问题.这就是欧拉对七桥问题建立起来的数学模型.
[数学问题的解决]
欧拉注意到,如果这样的图形能一笔画成,那么除去起点和终点外,其他的点都是“经过点”.“经过点”的特征是:只要从一条线进入这个点,就要从另一条线离开这个点.有进无出,只能是终点;有出无进,只能是起点.若以某一点为端点的线有偶数条,则称该点为偶点;否则称为奇点.显然“经过点”是偶点.如果起点和终点是同一个点,那么这个点也是偶点.
一笔画定理:一个由点和线组成的图形能一笔画完,必须符合以下两个条件:
(1)图形是连在一起的,即是连通图形;
(2)图形中的奇点个数为0或2.
[用数学结论解答原问题]
在七桥问题中,四个点全是奇点,不能一笔画,即不可能一次无重复地走完七座桥.
1741年,欧拉的相关论文发表在《圣彼得堡科学院通讯》上,开创了图论和拓扑学两门新的学科.
欧拉对实际问题进行抽象概括,用数学的语言(模型)把实际问题转化为数学问题,又用数学的思想方法分析、解决了这个问题,这个过程就是数学建模.
[用数学结论解答相关问题]
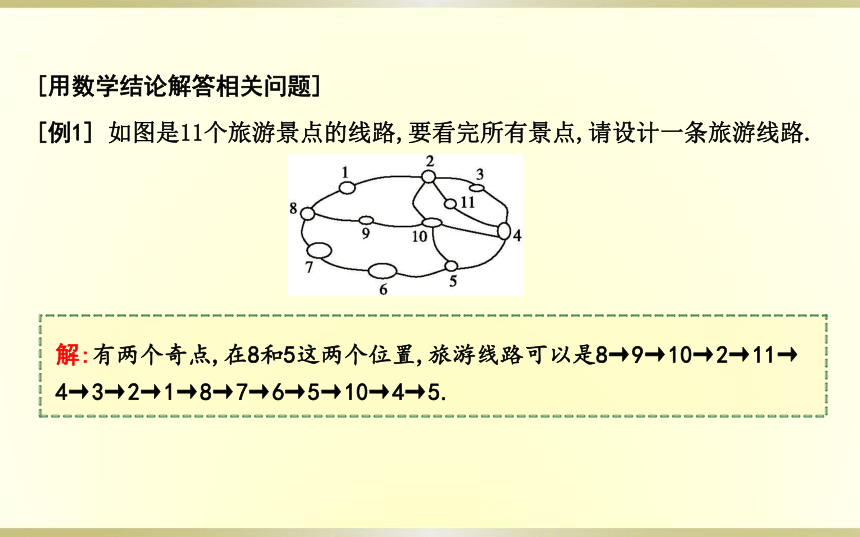
[例1] 如图是11个旅游景点的线路,要看完所有景点,请设计一条旅游线路.
解:有两个奇点,在8和5这两个位置,旅游线路可以是8→9→10→2→11→
4→3→2→1→8→7→6→5→10→4→5.
探究点二
实例探究 数学建模的主要步骤
[提出问题]
在一个十字路口,每次绿灯亮的时长为15 s,那么,每次绿灯亮时,在一条直行道路上能有多少辆汽车通过此十字路口
[建立模型]
这个问题涉及车长、车距、车速、堵塞的干扰等多种因素.而不同型号车的车长是不同的,驾驶员的习惯不同也会使车距、车速不同,行人和非机动车的干扰因素复杂且不确定.面对这些不同和不确定,就需要作出假设.例如,虽然通过路口的车辆各种各样,但多数是小轿车,因此这次建模就只考虑小轿车的情况,它们的长度差距不大,可以假设车辆长度都相同.
这是建模的重要环节——假设.
经过对相关因素的分析,可以作出有利于建立模型、基本符合实际情况的几个假设:
(1)通过路口的车辆长度都相等;
(2)等待时,前后相邻两辆车的车距都相等;
(3)绿灯亮后,汽车都是在静止状态下匀加速启动;
(4)前一辆车启动后,下一辆车启动的延时时间相等;
(5)车辆行驶秩序良好,不会发生堵塞.
将车辆长度记作l,车距记作d,经过实际调查,取l=5 m,d=2 m较为合理.
另据调查,一般的汽车按照十字路口的加速状态,10 s内可从静止加速到
21 m/s,加速度记作a,计算可得a=2.1 m/s2.为了简化,这里取a=2 m/s2.汽车加速到最高限速后,便以这个最高限速行驶.
问题中涉及的数据要建模者收集
[求解模型]
代入各个量的参数值,可以计算出绿灯亮至15 s时若干辆汽车的位置,如表.
汽车
序号 1 2 3 4 5 6 7 8
位置
/ m 124.6 106.5 88.4 70.3 52.2 34.1 16.0 -2.1
由表可见,绿灯亮至15 s时,第7辆车已经驶过停车线 16.0 m,而第8辆车还距停车线2.1 m,没有通过.因此,15 s的绿灯亮时最多可以通过7辆车.
[检验结果]
到十字路口实地调查,对结论做检验.若没有明显误差,就可以使用这个模
型.否则,再修改假设,重新建模.
方法总结
数学建模的一般步骤
(1)提出问题
实际情境中的问题往往是模糊的和笼统的,原始的问题往往是一个希望得到优化的期待,或是某个不良现象的消失,这就需要透过现象,明确地提出问题.
(2)建立模型
在一定的知识积累的基础上,预测建立的数学模型,抓住主要因素,摒弃次要因素,做出适当简化和假设.
在假设的基础上,用数学概念表示实际问题,用数学结构反映实际问题中各个量之间的关系.从不同角度、用不同知识表示同样的问题,就会得到不同的模型.
(3)求解模型
这个过程是求解数学问题,值得注意的是,如果目标是求值,一般不容易求得精确值,这就要根据需要求近似解.
(4)检验结果
用实际现象或数据检验求得的解是否符合实际.如果不符合实际情况,就要重新建模.
[拓展升华]
(一)数学应用题的特点
我们常把来源于客观世界,具有实际意义或实际背景,要通过数学建模的方法将问题转化为数学形式表示,从而获得解决的一类数学问题叫作数学应用题.数学应用题具有如下特点:
第一,数学应用题的本身具有实际意义或实际背景.这里的实际是指生产实际、社会实际、生活实际等现实世界的各个方面的实际.如与课本知识密切联系的源于实际生活的应用题;与横向络交汇点有联系的应用题;与现代科技发展、社会市场经济、环境保护、时事政治等有关的应用题等.
第二,数学应用题的求解需要采用数学建模的方法,使所求问题数学化,即将问题转化成数学形式来表示后再求解.
第三,数学应用题涉及的知识点多,是对综合运用数学知识和方法解决实际问题能力的检验,考查的是学生的综合能力,涉及的知识点一般在三个以上,如果某一知识点掌握不好,很难将问题正确解答.
第四,数学应用题的命题没有固定的模式或类别.往往是一种新颖的实际背景,难于进行题型模式训练,用“题海战术”无法解决变化多端的实际问题.必须依靠真实的能力来解题,对综合能力的考查更具有真实性、有效性.因此它具有广阔的发展空间和潜力.
(二)数学应用题如何建模
建立数学模型是解答数学应用题的关键.建立数学模型可分为以下几个层次:
第一层次:直接建模.
根据题设条件,套用现成的数学公式、定理等数学模型,注解图为:将题设条件翻译成数学表示形式.
应用题审题题设条件代入数学模型求解选定可直接运用的数学模型.
第二层次:多重建模.对复杂的关系进行提炼加工,忽略次要因素,建立若干个数学模型方能解决问题.
第三层次:假设建模.要进行分析、加工和作出假设,然后才能建立数学模型.如研究十字路口车流量问题,假设车流平稳,没有突发事件等才能建模.
(三)建立数学模型应具备的能力
从实际问题中建立数学模型,解决数学问题从而解决实际问题,这一全过程的关键是建立数学模型能力的强弱,直接关系到数学应用题的解题质量,同时也体现了综合能力.
1.提高分析、理解、阅读能力
阅读理解能力是数学建模的前提,数学应用题一般都创设一个新的背景,也针对问题本身使用一些专门术语,并给出即时定义.
2.强化将文字语言叙述、翻译成数学符号语言的能力
将数学应用题中所有表示数量关系的文字、图象语言翻译成数学符号语言,即数、式子、方程、不等式、函数等,这种译释能力是数学建模的基础性
工作.
例如:一种产品原来的成本为a元,在今后几年内,计划使成本平均每一年比上一年降低p%,经过五年后的成本为多少
将题中给出的文字翻译成符号语言,即成本y=a(1-p%)5.
3.增强选择数学模型的能力
选择数学模型是数学能力的反映.数学模型的建立有多种方法,怎样选择一个最佳的模型,体现数学能力的强弱.建立数学模型主要涉及方程、函数、不等式、数列通项公式、求和公式、曲线方程等类型.结合教学内容,以函数建模为例,以下为实际问题所选择的数学模型:
一次函数:成本、利润、销售收入等.
二次函数:优化问题、用料最省问题、造价最低、利润最大等.
幂函数、指数函数、对数函数:细胞分裂、生物繁殖等.
三角函数:测量、交通流量、力学问题等.
4.加强数学运算能力
数学应用题一般运算量较大、较复杂,且有近似计算.有的尽管思路正确、建模合理,但计算能力欠缺,就会前功尽弃.所以加强数学运算推理能力是使数学建模正确求解的关键所在,忽视运算能力,特别是计算能力的培养,只重视推理过程,不重视计算过程的做法是不可取的.
利用数学建模解数学应用题对于多角度、多层次、多侧面思考问题,培养学生发散思维能力是很有益的,是提高学生素质,进行素质教育的一条有效途径.同时数学建模的应用也是科学实践,有利于实践能力的培养,是实施素质教育所必需的,需要引起教育工作者的足够重视.
(四)数学建模解应用题举例
[例2] 你是否注意到有些建筑物的窗户是双层的,即窗户上装两层玻璃且中间留有一定空隙,如图(1)所示,两层厚度为d的玻璃夹着一层厚度为l的空气.据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如图(2),玻璃厚度为2d)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.
模型假设:
(1)热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的.
(2)室内温度T1和室外温度T2保持不变,热传导过程已处于稳定状态,即沿热传导方向,单位时间通过单位面积的热量是常数.
(3)玻璃材料均匀,热传导系数是常数.
从有关资料可知,常用玻璃的热传导系数为k1=4×10-3~8×10-3J/cm·s·
kW·h,不流通、干燥空气的热传导系数为k2=2.5×10-4 J/cm·s·kW·h.
则保温效果最好的双层玻璃的型号是( )
(A)A型 (B)B型 (C)C型 (D)D型
型号 每层玻璃厚度d/cm 玻璃间夹空气层厚度l/cm
A型 0.4 3
B型 0.3 4
C型 0.5 3
D型 0.4 4
探究点三
数学建模活动的主要过程
中学的“数学建模活动”是运用数学模型思想解决实际问题的综合实践活动,以课题研究形式开展,可以小组合作,也可以独立完成.课题研究的过程包括“选题、开题、做题、结题”四个环节.选题就是选定研究的问题,开题是进一步明确研究的问题和设计解决问题的方案,做题就是研究者(研究小组)建立数学模型、用数学解决实际问题的实践活动,结题是研究小组向老师和同学们报告研究成果、进行答辩的过程,一般来讲,结题会是结题的基本形式.一项研究完成之后,要写出结题报告.
[数学建模活动举例]
[例3] 在商场中,我们经常可以看到同一种商品会有多种大小不同的型号,其价格也各不相同.对比型号和价格,我们很容易发现:当商品的“量”增加时,价格也会增加;但是价格的增加与“量”的增加是不成比例的,也就是说买的商品的“量”越多,商品的平均价格越低,有人认为这是商家的营销策略,买得越多越划算,这样顾客往往倾向于购买大包装的商品.大包装的商品真的是薄利多销吗
就这一问题通过调查、分析、研究,完成选题、开题报告.
解:
要解决
的问题 到商场买牙膏,从划算的角度讲,同一品牌的牙膏我们是买小包装的好,还是大包装的好呢
解决
问题
的方法 同一品牌的牙膏形状是相似的,通过比例建立价格与质量的函数关系
相关
问题
分析
及其
假设 我们设商品的价格为y(元),质量为x(g),看能否找出y与x的函数关系式y=f(x).为了方便叙述,我们引入“∝”这一符号,当y与x成比例,即y=kx(k为常数)时,记作y∝x
结果
检验 将x=120代入,得y≈21.57,与实际价格21.60元相差0.03;再将x=180代入,得y≈28.78,与实际价格28.30元相差0.48元.
因此,我们推导出来的函数表达式还是比较准确的
小组成
员的分
工和各
自的主
要贡献 全组共同制订研究计划,商讨并确定数学模型,另分工如下:
同学甲,组长,侧重组织讨论,把握工作方向;
同学乙、丙,侧重信息采集、数据计算整理;
同学丁,侧重讨论记录、报告撰写、结果复核
反思与
拓展 在以上推导过程中,我们只考虑了生产和包装两种主要的成本,如果将运输成本、超市上架费、网站仓储费等因素也考虑进去,可能结果会更准确,但是模型也会复杂很多,可操作性就差了.另外,商品包装的材质也会对价格造成较大的影响,比如同一品牌的巧克力,可能会有普通包装、精品包装和礼品包装三种,这时如果只考虑分量对价格的影响,显然是不合适的
研究的
收获和
感受,
得到的
帮助和
致谢 对自己确定相关因素和“寻找”数据有了切身感受.分工合作使我们理解了未来的学习和工作模式,学会了向别人学习,同时积极表达自己的想法.感谢我们的数学老师和家长提供的参考意见和对我们的鼓励
主要参
考文献 《从课程标准到课堂教学:中学教学建模与探究》(张思明主编)
变式训练3-1:针对“甲市区道路交通流量随时间变化规律”这一选题进行分析、思考,完成其开题报告.
解:
要解决的问题 随着甲市的不断发展,交通成了饱受关注的话题,那么甲市区主要道路交通流量随时间变化有什么样的规律
选题的原
因及意义 为市民日常出行乃至相关部门的政策制定提供参考
建模问题的
可行性分析 时间和车流量满足一定的函数关系
基本模型、解
决问题的大体
思路和步骤 观测某主干道每3分钟内通过的车流量,进行分析比较,时间为自变量x(单位:小时),车流量为因变量y(单位:辆/3分)
预期结果和结
果呈现方式 一个能够反映时间与车流量的函数模型,一份有求解过程的文字报告
成员和分工 全组共同制订研究计划商讨确定数学模型
同学甲(组长,侧重组织讨论,把握工作方向)
同学乙、丙(侧重信息采集、数据计算整理)
同学丁(侧重讨论记录、报告撰写、结果复核)
参考文献 《甲市交通状况的分析与预测》
百度地图http://map.
备用例题
[例1] 某工艺公司要对某种工艺品深加工,已知每个工艺品进价为20元,每个工艺品的加工费为n元,销售单价为x元.根据市场调查,须有n∈[3,6],x∈
[26,32],x∈N,同时日销售量m(单位:个)与10-x成正比.当每个工艺品的销售单价为29元时,日销售量为1 000个.
(1)写出日销售利润y(单位:元)与x的函数关系式;
(2)当每个工艺品的加工费用为5元时,要使该公司的日销售利润为100万元,试确定销售单价x的值.(提示:函数y=10x-26与y=x-25的图象在[26,32]上有且只有一个公共点)
解:(2)当n=5时,由y=(x-25)1032-x=100×104=106,
整理得x-25=10x-26.
因为函数y=10x-26与y=x-25的图象在[26,32]上有且只有一个公共点,且当x=26时,等式成立,
所以x=26是方程x-25=10x-26唯一的根,
所以销售单价为26元时,该公司的日销售利润为100万元.
(1)把利润表示为年产量的函数;
(2)年产量为多少时,企业所得利润最大
(3)年产量为多少时,企业才不亏本(不赔钱)
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群的年增长量达到最大值时,求k的取值范围.
第八章 数学建模活动(一)
§1 走近数学建模
§2 数学建模的主要步骤
§3 数学建模活动的主要过程
核心知识目标 核心素养目标
1.了解熟悉数学模型的实际背景及其数学描述,了解数学模型中的参数、结论的实际含义.
2.知道数学建模的一般步骤包括提出问题、建立模型、求解模型、检验结果.能够在熟悉的实际情境中,模仿学过的数学建模过程解决问题.
3.对于学过的数学模型,能够举例说明建模的意义,体会其蕴含的数学思想;感悟数学表达对数学建模的重要性.在交流的过程中,能够借助或引用已有数学建模的结果说明问题.
4.知道数学建模活动的主要过程包括选题、开题、做题、结题,能够选择简单的实际问题,完成数学建模活动. 1.通过在综合的情境中,运用数学思维进行分析,发现情境中的数学关系,提出数学问题,运用数学建模的一般方法和相关知识,建立数学模型,解决问题,培养数学建模素养.
2.通过理解数学建模的意义和作用,运用数学语言,清晰、准确地表达数学建模的过程和结果,在交流的过程中,能够通过数学建模的结论和思想阐释科学规律和社会现象,培养数学运算、逻辑推理和数据分析素养.
知识探究·素养培育
探究点一
走近数学建模
[实际问题 哥尼斯堡七桥问题]
普莱格尔河穿过美丽的哥尼斯堡城(现为俄罗斯的加里宁格勒).普莱格尔河有两个支流,在城市中心汇成大河,中间是岛区,在河上有七座桥,如图.
岛上有古老的哥尼斯堡大学、知名的大教堂,居民经常到河岸和桥上散步.在18世纪初的一天,有人突发奇想:如何才能走过这七座桥,而每座桥都只能经过一次,最后又回到原来的出发点 人们开始沉迷于这个问题,在桥上来来回回不知走了多少次,却始终不得其解.这就是著名的哥尼斯堡七桥问题.
[实际问题的数学表述]
七桥问题引起了数学家欧拉的极大兴趣.他想:经过这么多人的努力都没有找到一次不重复走完七座桥的路径,会不会根本不存在这样的走法
首先,欧拉想到的是列举法,就是把所有的走法都一一列出来,再一个一个验证.但是,他很快发现这样做太麻烦了,因为对七座桥的不同走法就有5 000多种,并且这种方法不具有通用性.
经过反复思考,欧拉想到:岛的形状、大小,以及桥的长短、宽窄并不影响结果,重要的是陆地、桥与岛这三者之间的位置关系.不妨把图中被河隔开的4块陆地看作4个点,连接陆地的7座桥看作7条线,就得到如图的图形.实际问题中的陆地、河流和桥梁景观就不见了,七桥问题就变成能否一笔画出此图形的问题.这就是欧拉对七桥问题建立起来的数学模型.
[数学问题的解决]
欧拉注意到,如果这样的图形能一笔画成,那么除去起点和终点外,其他的点都是“经过点”.“经过点”的特征是:只要从一条线进入这个点,就要从另一条线离开这个点.有进无出,只能是终点;有出无进,只能是起点.若以某一点为端点的线有偶数条,则称该点为偶点;否则称为奇点.显然“经过点”是偶点.如果起点和终点是同一个点,那么这个点也是偶点.
一笔画定理:一个由点和线组成的图形能一笔画完,必须符合以下两个条件:
(1)图形是连在一起的,即是连通图形;
(2)图形中的奇点个数为0或2.
[用数学结论解答原问题]
在七桥问题中,四个点全是奇点,不能一笔画,即不可能一次无重复地走完七座桥.
1741年,欧拉的相关论文发表在《圣彼得堡科学院通讯》上,开创了图论和拓扑学两门新的学科.
欧拉对实际问题进行抽象概括,用数学的语言(模型)把实际问题转化为数学问题,又用数学的思想方法分析、解决了这个问题,这个过程就是数学建模.
[用数学结论解答相关问题]
[例1] 如图是11个旅游景点的线路,要看完所有景点,请设计一条旅游线路.
解:有两个奇点,在8和5这两个位置,旅游线路可以是8→9→10→2→11→
4→3→2→1→8→7→6→5→10→4→5.
探究点二
实例探究 数学建模的主要步骤
[提出问题]
在一个十字路口,每次绿灯亮的时长为15 s,那么,每次绿灯亮时,在一条直行道路上能有多少辆汽车通过此十字路口
[建立模型]
这个问题涉及车长、车距、车速、堵塞的干扰等多种因素.而不同型号车的车长是不同的,驾驶员的习惯不同也会使车距、车速不同,行人和非机动车的干扰因素复杂且不确定.面对这些不同和不确定,就需要作出假设.例如,虽然通过路口的车辆各种各样,但多数是小轿车,因此这次建模就只考虑小轿车的情况,它们的长度差距不大,可以假设车辆长度都相同.
这是建模的重要环节——假设.
经过对相关因素的分析,可以作出有利于建立模型、基本符合实际情况的几个假设:
(1)通过路口的车辆长度都相等;
(2)等待时,前后相邻两辆车的车距都相等;
(3)绿灯亮后,汽车都是在静止状态下匀加速启动;
(4)前一辆车启动后,下一辆车启动的延时时间相等;
(5)车辆行驶秩序良好,不会发生堵塞.
将车辆长度记作l,车距记作d,经过实际调查,取l=5 m,d=2 m较为合理.
另据调查,一般的汽车按照十字路口的加速状态,10 s内可从静止加速到
21 m/s,加速度记作a,计算可得a=2.1 m/s2.为了简化,这里取a=2 m/s2.汽车加速到最高限速后,便以这个最高限速行驶.
问题中涉及的数据要建模者收集
[求解模型]
代入各个量的参数值,可以计算出绿灯亮至15 s时若干辆汽车的位置,如表.
汽车
序号 1 2 3 4 5 6 7 8
位置
/ m 124.6 106.5 88.4 70.3 52.2 34.1 16.0 -2.1
由表可见,绿灯亮至15 s时,第7辆车已经驶过停车线 16.0 m,而第8辆车还距停车线2.1 m,没有通过.因此,15 s的绿灯亮时最多可以通过7辆车.
[检验结果]
到十字路口实地调查,对结论做检验.若没有明显误差,就可以使用这个模
型.否则,再修改假设,重新建模.
方法总结
数学建模的一般步骤
(1)提出问题
实际情境中的问题往往是模糊的和笼统的,原始的问题往往是一个希望得到优化的期待,或是某个不良现象的消失,这就需要透过现象,明确地提出问题.
(2)建立模型
在一定的知识积累的基础上,预测建立的数学模型,抓住主要因素,摒弃次要因素,做出适当简化和假设.
在假设的基础上,用数学概念表示实际问题,用数学结构反映实际问题中各个量之间的关系.从不同角度、用不同知识表示同样的问题,就会得到不同的模型.
(3)求解模型
这个过程是求解数学问题,值得注意的是,如果目标是求值,一般不容易求得精确值,这就要根据需要求近似解.
(4)检验结果
用实际现象或数据检验求得的解是否符合实际.如果不符合实际情况,就要重新建模.
[拓展升华]
(一)数学应用题的特点
我们常把来源于客观世界,具有实际意义或实际背景,要通过数学建模的方法将问题转化为数学形式表示,从而获得解决的一类数学问题叫作数学应用题.数学应用题具有如下特点:
第一,数学应用题的本身具有实际意义或实际背景.这里的实际是指生产实际、社会实际、生活实际等现实世界的各个方面的实际.如与课本知识密切联系的源于实际生活的应用题;与横向络交汇点有联系的应用题;与现代科技发展、社会市场经济、环境保护、时事政治等有关的应用题等.
第二,数学应用题的求解需要采用数学建模的方法,使所求问题数学化,即将问题转化成数学形式来表示后再求解.
第三,数学应用题涉及的知识点多,是对综合运用数学知识和方法解决实际问题能力的检验,考查的是学生的综合能力,涉及的知识点一般在三个以上,如果某一知识点掌握不好,很难将问题正确解答.
第四,数学应用题的命题没有固定的模式或类别.往往是一种新颖的实际背景,难于进行题型模式训练,用“题海战术”无法解决变化多端的实际问题.必须依靠真实的能力来解题,对综合能力的考查更具有真实性、有效性.因此它具有广阔的发展空间和潜力.
(二)数学应用题如何建模
建立数学模型是解答数学应用题的关键.建立数学模型可分为以下几个层次:
第一层次:直接建模.
根据题设条件,套用现成的数学公式、定理等数学模型,注解图为:将题设条件翻译成数学表示形式.
应用题审题题设条件代入数学模型求解选定可直接运用的数学模型.
第二层次:多重建模.对复杂的关系进行提炼加工,忽略次要因素,建立若干个数学模型方能解决问题.
第三层次:假设建模.要进行分析、加工和作出假设,然后才能建立数学模型.如研究十字路口车流量问题,假设车流平稳,没有突发事件等才能建模.
(三)建立数学模型应具备的能力
从实际问题中建立数学模型,解决数学问题从而解决实际问题,这一全过程的关键是建立数学模型能力的强弱,直接关系到数学应用题的解题质量,同时也体现了综合能力.
1.提高分析、理解、阅读能力
阅读理解能力是数学建模的前提,数学应用题一般都创设一个新的背景,也针对问题本身使用一些专门术语,并给出即时定义.
2.强化将文字语言叙述、翻译成数学符号语言的能力
将数学应用题中所有表示数量关系的文字、图象语言翻译成数学符号语言,即数、式子、方程、不等式、函数等,这种译释能力是数学建模的基础性
工作.
例如:一种产品原来的成本为a元,在今后几年内,计划使成本平均每一年比上一年降低p%,经过五年后的成本为多少
将题中给出的文字翻译成符号语言,即成本y=a(1-p%)5.
3.增强选择数学模型的能力
选择数学模型是数学能力的反映.数学模型的建立有多种方法,怎样选择一个最佳的模型,体现数学能力的强弱.建立数学模型主要涉及方程、函数、不等式、数列通项公式、求和公式、曲线方程等类型.结合教学内容,以函数建模为例,以下为实际问题所选择的数学模型:
一次函数:成本、利润、销售收入等.
二次函数:优化问题、用料最省问题、造价最低、利润最大等.
幂函数、指数函数、对数函数:细胞分裂、生物繁殖等.
三角函数:测量、交通流量、力学问题等.
4.加强数学运算能力
数学应用题一般运算量较大、较复杂,且有近似计算.有的尽管思路正确、建模合理,但计算能力欠缺,就会前功尽弃.所以加强数学运算推理能力是使数学建模正确求解的关键所在,忽视运算能力,特别是计算能力的培养,只重视推理过程,不重视计算过程的做法是不可取的.
利用数学建模解数学应用题对于多角度、多层次、多侧面思考问题,培养学生发散思维能力是很有益的,是提高学生素质,进行素质教育的一条有效途径.同时数学建模的应用也是科学实践,有利于实践能力的培养,是实施素质教育所必需的,需要引起教育工作者的足够重视.
(四)数学建模解应用题举例
[例2] 你是否注意到有些建筑物的窗户是双层的,即窗户上装两层玻璃且中间留有一定空隙,如图(1)所示,两层厚度为d的玻璃夹着一层厚度为l的空气.据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如图(2),玻璃厚度为2d)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.
模型假设:
(1)热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的.
(2)室内温度T1和室外温度T2保持不变,热传导过程已处于稳定状态,即沿热传导方向,单位时间通过单位面积的热量是常数.
(3)玻璃材料均匀,热传导系数是常数.
从有关资料可知,常用玻璃的热传导系数为k1=4×10-3~8×10-3J/cm·s·
kW·h,不流通、干燥空气的热传导系数为k2=2.5×10-4 J/cm·s·kW·h.
则保温效果最好的双层玻璃的型号是( )
(A)A型 (B)B型 (C)C型 (D)D型
型号 每层玻璃厚度d/cm 玻璃间夹空气层厚度l/cm
A型 0.4 3
B型 0.3 4
C型 0.5 3
D型 0.4 4
探究点三
数学建模活动的主要过程
中学的“数学建模活动”是运用数学模型思想解决实际问题的综合实践活动,以课题研究形式开展,可以小组合作,也可以独立完成.课题研究的过程包括“选题、开题、做题、结题”四个环节.选题就是选定研究的问题,开题是进一步明确研究的问题和设计解决问题的方案,做题就是研究者(研究小组)建立数学模型、用数学解决实际问题的实践活动,结题是研究小组向老师和同学们报告研究成果、进行答辩的过程,一般来讲,结题会是结题的基本形式.一项研究完成之后,要写出结题报告.
[数学建模活动举例]
[例3] 在商场中,我们经常可以看到同一种商品会有多种大小不同的型号,其价格也各不相同.对比型号和价格,我们很容易发现:当商品的“量”增加时,价格也会增加;但是价格的增加与“量”的增加是不成比例的,也就是说买的商品的“量”越多,商品的平均价格越低,有人认为这是商家的营销策略,买得越多越划算,这样顾客往往倾向于购买大包装的商品.大包装的商品真的是薄利多销吗
就这一问题通过调查、分析、研究,完成选题、开题报告.
解:
要解决
的问题 到商场买牙膏,从划算的角度讲,同一品牌的牙膏我们是买小包装的好,还是大包装的好呢
解决
问题
的方法 同一品牌的牙膏形状是相似的,通过比例建立价格与质量的函数关系
相关
问题
分析
及其
假设 我们设商品的价格为y(元),质量为x(g),看能否找出y与x的函数关系式y=f(x).为了方便叙述,我们引入“∝”这一符号,当y与x成比例,即y=kx(k为常数)时,记作y∝x
结果
检验 将x=120代入,得y≈21.57,与实际价格21.60元相差0.03;再将x=180代入,得y≈28.78,与实际价格28.30元相差0.48元.
因此,我们推导出来的函数表达式还是比较准确的
小组成
员的分
工和各
自的主
要贡献 全组共同制订研究计划,商讨并确定数学模型,另分工如下:
同学甲,组长,侧重组织讨论,把握工作方向;
同学乙、丙,侧重信息采集、数据计算整理;
同学丁,侧重讨论记录、报告撰写、结果复核
反思与
拓展 在以上推导过程中,我们只考虑了生产和包装两种主要的成本,如果将运输成本、超市上架费、网站仓储费等因素也考虑进去,可能结果会更准确,但是模型也会复杂很多,可操作性就差了.另外,商品包装的材质也会对价格造成较大的影响,比如同一品牌的巧克力,可能会有普通包装、精品包装和礼品包装三种,这时如果只考虑分量对价格的影响,显然是不合适的
研究的
收获和
感受,
得到的
帮助和
致谢 对自己确定相关因素和“寻找”数据有了切身感受.分工合作使我们理解了未来的学习和工作模式,学会了向别人学习,同时积极表达自己的想法.感谢我们的数学老师和家长提供的参考意见和对我们的鼓励
主要参
考文献 《从课程标准到课堂教学:中学教学建模与探究》(张思明主编)
变式训练3-1:针对“甲市区道路交通流量随时间变化规律”这一选题进行分析、思考,完成其开题报告.
解:
要解决的问题 随着甲市的不断发展,交通成了饱受关注的话题,那么甲市区主要道路交通流量随时间变化有什么样的规律
选题的原
因及意义 为市民日常出行乃至相关部门的政策制定提供参考
建模问题的
可行性分析 时间和车流量满足一定的函数关系
基本模型、解
决问题的大体
思路和步骤 观测某主干道每3分钟内通过的车流量,进行分析比较,时间为自变量x(单位:小时),车流量为因变量y(单位:辆/3分)
预期结果和结
果呈现方式 一个能够反映时间与车流量的函数模型,一份有求解过程的文字报告
成员和分工 全组共同制订研究计划商讨确定数学模型
同学甲(组长,侧重组织讨论,把握工作方向)
同学乙、丙(侧重信息采集、数据计算整理)
同学丁(侧重讨论记录、报告撰写、结果复核)
参考文献 《甲市交通状况的分析与预测》
百度地图http://map.
备用例题
[例1] 某工艺公司要对某种工艺品深加工,已知每个工艺品进价为20元,每个工艺品的加工费为n元,销售单价为x元.根据市场调查,须有n∈[3,6],x∈
[26,32],x∈N,同时日销售量m(单位:个)与10-x成正比.当每个工艺品的销售单价为29元时,日销售量为1 000个.
(1)写出日销售利润y(单位:元)与x的函数关系式;
(2)当每个工艺品的加工费用为5元时,要使该公司的日销售利润为100万元,试确定销售单价x的值.(提示:函数y=10x-26与y=x-25的图象在[26,32]上有且只有一个公共点)
解:(2)当n=5时,由y=(x-25)1032-x=100×104=106,
整理得x-25=10x-26.
因为函数y=10x-26与y=x-25的图象在[26,32]上有且只有一个公共点,且当x=26时,等式成立,
所以x=26是方程x-25=10x-26唯一的根,
所以销售单价为26元时,该公司的日销售利润为100万元.
(1)把利润表示为年产量的函数;
(2)年产量为多少时,企业所得利润最大
(3)年产量为多少时,企业才不亏本(不赔钱)
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群的年增长量达到最大值时,求k的取值范围.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
