中考总复习1(实数的概念)[下学期]
文档属性
| 名称 | 中考总复习1(实数的概念)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 446.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-02 17:56:00 | ||
图片预览







文档简介
课件26张PPT。中考复习准备好了吗?时刻准备着!2006年一、实数中考说明及中考全书1、实数课标要求 (有的放矢)(1)有理数
①理解有理数的意义,能用数轴上的点表示有理数,会比较有理数的大小。
②借助数轴理解相反数和绝对值的意义,会求有理数的相反数与 绝对值(绝对值符号内不含字母)。
③理解乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算以三步为主)。 ④理解有理数的运算律,并能运用运算律简化运算。
⑤能运用有理数的运算解决简单的问题。
⑥能对含有较大数字的信息作出合理的解释和推断。
(2)实数
①了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。 ②了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会用计算器求平方根和立方根。
③了解无理数和实数的概念,知道实数与数轴上的点一一对应。
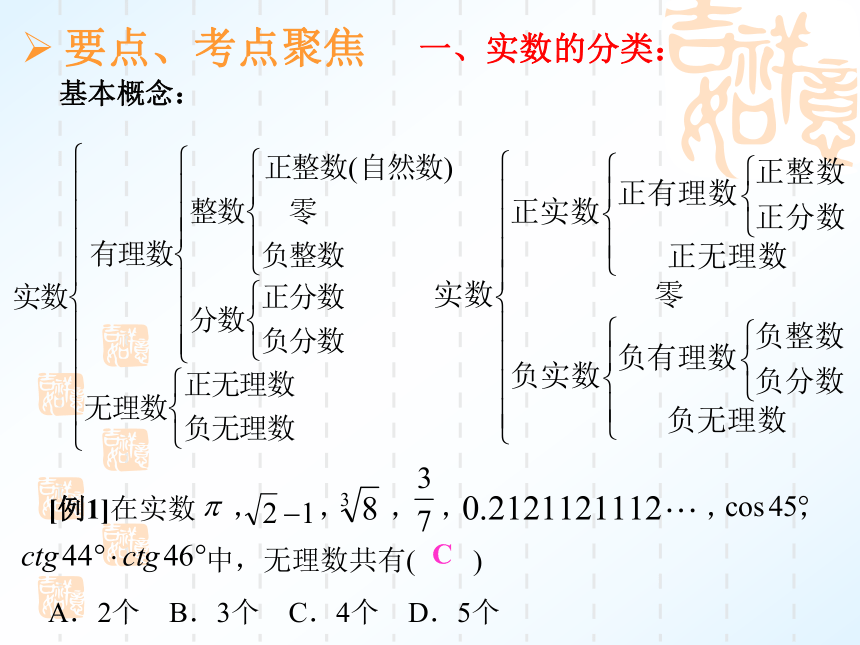
④能用有理数估计一个无理数的大致范围。 一、实数的分类:基本概念:[例1]在实数 , , , , , ,
中,无理数共有( )
A.2个 B.3个 C.4个 D.5个
C要点、考点聚焦一、有理数的基本概念1.负数:在正数前面加“—”的数;0既不是正数,也不是负数。判断:
1)a一定是正数;
2)-a一定是负数;
3)-(-a)一定大于0;
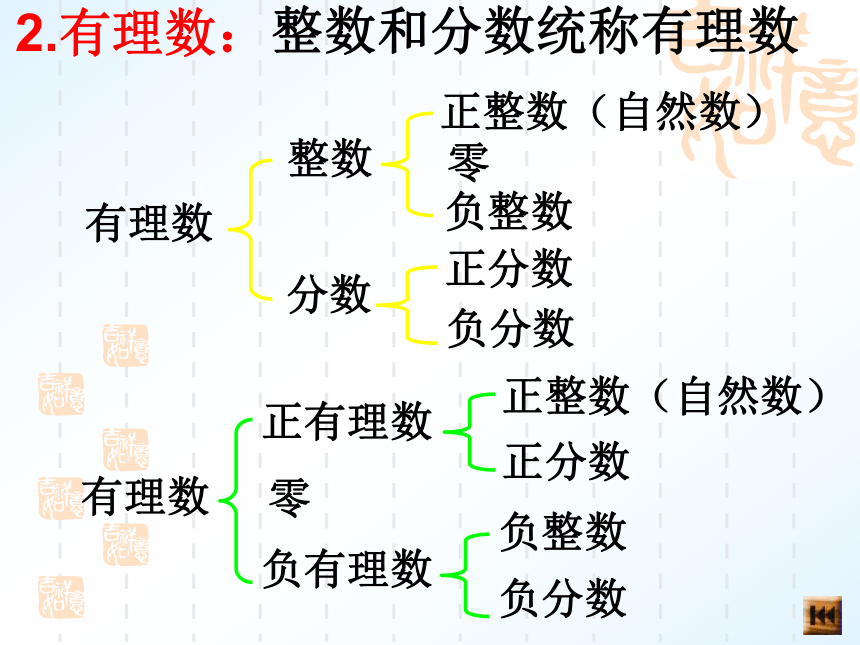
4)0是正整数。××××2.有理数: 整数和分数统称有理数有理数整数分数正整数(自然数) 零负整数正分数负分数有理数正有理数零负有理数正整数(自然数)正分数负整数负分数3.数 轴规定了原点、正方向和单位长度的直线.1)在数轴上表示的两个数,
右边的数总比左边的数大;2)正数都大于0,负数都小于0;
正数大于一切负数;3)所有有理数都可以用数轴上
的点表示。4.相反数 只有符号不同的两个数,
其中一个是另一个的相反数。 1)数a的相反数是-a2)0的相反数是0. -22-443)若a、b互为相反数,则a+b=0. (a是任意一个有理数);5.倒 数 乘积是1的两个数互为倒数 .1)a的倒数是 (a≠0); 3)若a与b互为倒数,则ab=1.2)0没有倒数 ;例:下列各数,哪两个数互为倒数?
8, ,-1,+(-8),1,6.绝对值一个数a的绝对值就是数轴上
表示数a的点与原点的距离。1)数a的绝对值记作︱a︱; a-a03) 对任何有理数a,总有︱a︱≥0.例2:3的相反数的倒数是 。 例3:a ,b ,c 在数轴上的位置如图所示,且 ,则 。 例4:已知:| a |=3,| b |=2,且 ab < 0,求 a-b 的值。 a =3, b =-2时, a-b=5 a =-3, b =2时, a-b=-57.有理数大小的比较1)可通过数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数;
2)两个负数,绝对值大的反而小。
即:若a<0,b<0,且︱a︱>︱b︱,
则a < b.课前热身1、 - 1/3的倒数是 ( )
A.3 B. - 3 C.1/3 D.-1/3 (2004北京)2、 的相反数是 ( )
A.-3 B. -1/3 C. 3 D. (2004广东) 3、两个相反数在数轴上的对应点在 的两侧且与
的距离相等。4、相反数是本身的数是 ;绝对值是本身的数是
;倒数是本身的数是 。BA原点原点0非负数±15、-(-4)的相反数是 ,(+8)是 的相反数 6、(1)如果零上5℃记作5℃,则零下2℃记作
(2) 如果上升10m记作10m,那么-5m表示
(3)比海平面低35m的地方,它的高度是海拔
7、a、b互为相反数,c与d互为倒数则a+1+b+cd=
。8、实数a,b,c,d在数轴上的对应点如图所示,则它们
从小到大的顺序是 。其中:2c (3)若 ,且xy>0,x+y= 。 例2、把下列各数填到相应的集合里:整数集合:{ }; 分数集合:{ }; 有理数集合: ; 无理数集合:{ }。 1/32 -;tan45°; - 3 3-1;3.14;22/7;sin30°;|-3.2|;-0.32·1· 3-1; ;3.14;22/7;sin30°;tan45°-3;-0.321;|-3.2| ;-π;0.100110001… 3或- 30.100110001例3、比较大小: 与例4、已知实数a、b在数轴上对应点的位置如图;
化简:解:
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+ =(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.例5、若求 的值。解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-4/3,b=3/4
∴a2003b2004=(-4/3)2003·(3/4)2004=-3/4
搞清实数的分类标准,尤其要弄懂无理数的三种常见形式:① ;②无限不循环小数,如0.1010010001……;③开方开不尽的数,如 等。
绝对值的性质——要注意正确区分数的三种情况,尤其是负数去掉绝对值应变为其相反数。
实数的大小比较应重点掌握作差法和作商法,才能更好地有的放矢。方法小结:有理数集合:{ }; 课时训练1、把下列各数填在相应的大括号内:整数集合:{ ……}; 奇数集合:{ ……}; 无理数集合:{ }。 -1,0, -1π,-,tan30°,2.1010010001… -1,,3.14,0, ,cos60°, 2、下列说法中,错误的个数是 ( )①无理数都是无限小数;②无理数都是开方开不尽的数;
③带根号的都是无理数;④无限小数都是无理数。 A.1个; B.2个; C.3个; D.4个。3、数轴上的点与( )一一对应。 A.整数; B.有理数; C.无理数; D.实数。4、下列运算正确的是 ( )A.B.C.D.CDA 5、计算2 - (-3)的结果是 ( ) -5 B.5C.1 D. -1(重庆2004年中考题)6、在1,-1,-2这三个数中,任意两数之和的最大值是 ( )
A.1 B.0 C. -1 D. -3(南京2004年中考题)BB7、 的绝对值等于 ,
的平方根等于 ,
的倒数是 。(黄冈2004年中考题)8.(海淀区2004) 2的相反数是
A. B. C.-2 D.2 9.(重庆市北碚区 2004 ) 的相反数是()
A B C -2 D 210.(青海省湟中县实验区2004 ) 的相反数的倒数是 . 祝同学们:金榜题名!愿我们:心想事成!再见!
①理解有理数的意义,能用数轴上的点表示有理数,会比较有理数的大小。
②借助数轴理解相反数和绝对值的意义,会求有理数的相反数与 绝对值(绝对值符号内不含字母)。
③理解乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算以三步为主)。 ④理解有理数的运算律,并能运用运算律简化运算。
⑤能运用有理数的运算解决简单的问题。
⑥能对含有较大数字的信息作出合理的解释和推断。
(2)实数
①了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。 ②了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会用计算器求平方根和立方根。
③了解无理数和实数的概念,知道实数与数轴上的点一一对应。
④能用有理数估计一个无理数的大致范围。 一、实数的分类:基本概念:[例1]在实数 , , , , , ,
中,无理数共有( )
A.2个 B.3个 C.4个 D.5个
C要点、考点聚焦一、有理数的基本概念1.负数:在正数前面加“—”的数;0既不是正数,也不是负数。判断:
1)a一定是正数;
2)-a一定是负数;
3)-(-a)一定大于0;
4)0是正整数。××××2.有理数: 整数和分数统称有理数有理数整数分数正整数(自然数) 零负整数正分数负分数有理数正有理数零负有理数正整数(自然数)正分数负整数负分数3.数 轴规定了原点、正方向和单位长度的直线.1)在数轴上表示的两个数,
右边的数总比左边的数大;2)正数都大于0,负数都小于0;
正数大于一切负数;3)所有有理数都可以用数轴上
的点表示。4.相反数 只有符号不同的两个数,
其中一个是另一个的相反数。 1)数a的相反数是-a2)0的相反数是0. -22-443)若a、b互为相反数,则a+b=0. (a是任意一个有理数);5.倒 数 乘积是1的两个数互为倒数 .1)a的倒数是 (a≠0); 3)若a与b互为倒数,则ab=1.2)0没有倒数 ;例:下列各数,哪两个数互为倒数?
8, ,-1,+(-8),1,6.绝对值一个数a的绝对值就是数轴上
表示数a的点与原点的距离。1)数a的绝对值记作︱a︱; a-a03) 对任何有理数a,总有︱a︱≥0.例2:3的相反数的倒数是 。 例3:a ,b ,c 在数轴上的位置如图所示,且 ,则 。 例4:已知:| a |=3,| b |=2,且 ab < 0,求 a-b 的值。 a =3, b =-2时, a-b=5 a =-3, b =2时, a-b=-57.有理数大小的比较1)可通过数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数;
2)两个负数,绝对值大的反而小。
即:若a<0,b<0,且︱a︱>︱b︱,
则a < b.课前热身1、 - 1/3的倒数是 ( )
A.3 B. - 3 C.1/3 D.-1/3 (2004北京)2、 的相反数是 ( )
A.-3 B. -1/3 C. 3 D. (2004广东) 3、两个相反数在数轴上的对应点在 的两侧且与
的距离相等。4、相反数是本身的数是 ;绝对值是本身的数是
;倒数是本身的数是 。BA原点原点0非负数±15、-(-4)的相反数是 ,(+8)是 的相反数 6、(1)如果零上5℃记作5℃,则零下2℃记作
(2) 如果上升10m记作10m,那么-5m表示
(3)比海平面低35m的地方,它的高度是海拔
7、a、b互为相反数,c与d互为倒数则a+1+b+cd=
。8、实数a,b,c,d在数轴上的对应点如图所示,则它们
从小到大的顺序是 。其中:2c
化简:解:
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+ =(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.例5、若求 的值。解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-4/3,b=3/4
∴a2003b2004=(-4/3)2003·(3/4)2004=-3/4
搞清实数的分类标准,尤其要弄懂无理数的三种常见形式:① ;②无限不循环小数,如0.1010010001……;③开方开不尽的数,如 等。
绝对值的性质——要注意正确区分数的三种情况,尤其是负数去掉绝对值应变为其相反数。
实数的大小比较应重点掌握作差法和作商法,才能更好地有的放矢。方法小结:有理数集合:{ }; 课时训练1、把下列各数填在相应的大括号内:整数集合:{ ……}; 奇数集合:{ ……}; 无理数集合:{ }。 -1,0, -1π,-,tan30°,2.1010010001… -1,,3.14,0, ,cos60°, 2、下列说法中,错误的个数是 ( )①无理数都是无限小数;②无理数都是开方开不尽的数;
③带根号的都是无理数;④无限小数都是无理数。 A.1个; B.2个; C.3个; D.4个。3、数轴上的点与( )一一对应。 A.整数; B.有理数; C.无理数; D.实数。4、下列运算正确的是 ( )A.B.C.D.CDA 5、计算2 - (-3)的结果是 ( ) -5 B.5C.1 D. -1(重庆2004年中考题)6、在1,-1,-2这三个数中,任意两数之和的最大值是 ( )
A.1 B.0 C. -1 D. -3(南京2004年中考题)BB7、 的绝对值等于 ,
的平方根等于 ,
的倒数是 。(黄冈2004年中考题)8.(海淀区2004) 2的相反数是
A. B. C.-2 D.2 9.(重庆市北碚区 2004 ) 的相反数是()
A B C -2 D 210.(青海省湟中县实验区2004 ) 的相反数的倒数是 . 祝同学们:金榜题名!愿我们:心想事成!再见!
