13.4 最短路径问题 课件(共24张PPT)
文档属性
| 名称 | 13.4 最短路径问题 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 992.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 19:41:49 | ||
图片预览




文档简介
(共24张PPT)
13.4 最短路径问题
人教版 八年级上册
由一个平面图形可以得到与它关于一条直线对称
的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于对称轴 的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
轴对称的性质
复习旧知
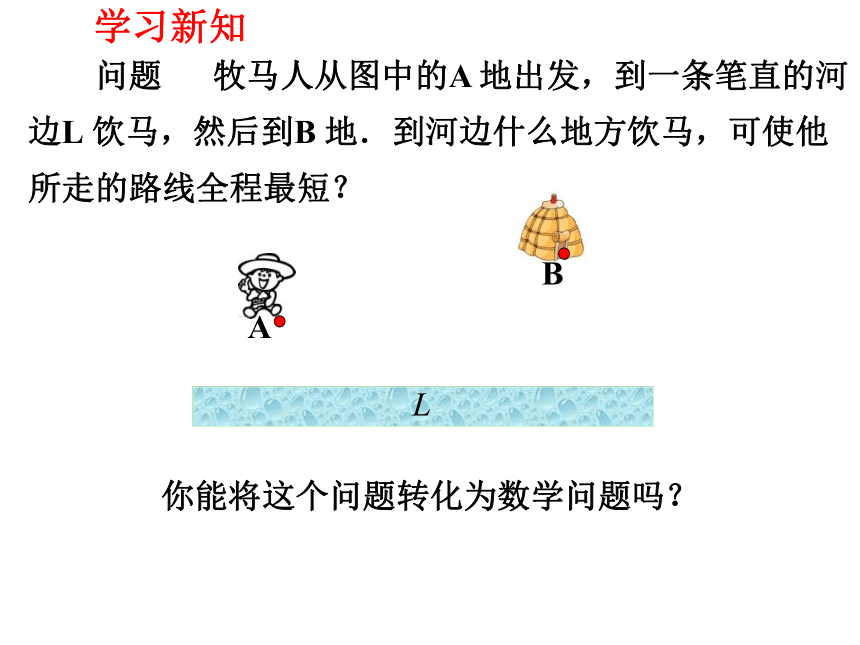
问题 牧马人从图中的A 地出发,到一条笔直的河边L 饮马,然后到B 地.到河边什么地方饮马,可使他所走的路线全程最短?
B
A
L
你能将这个问题转化为数学问题吗?
学习新知
B
A
L
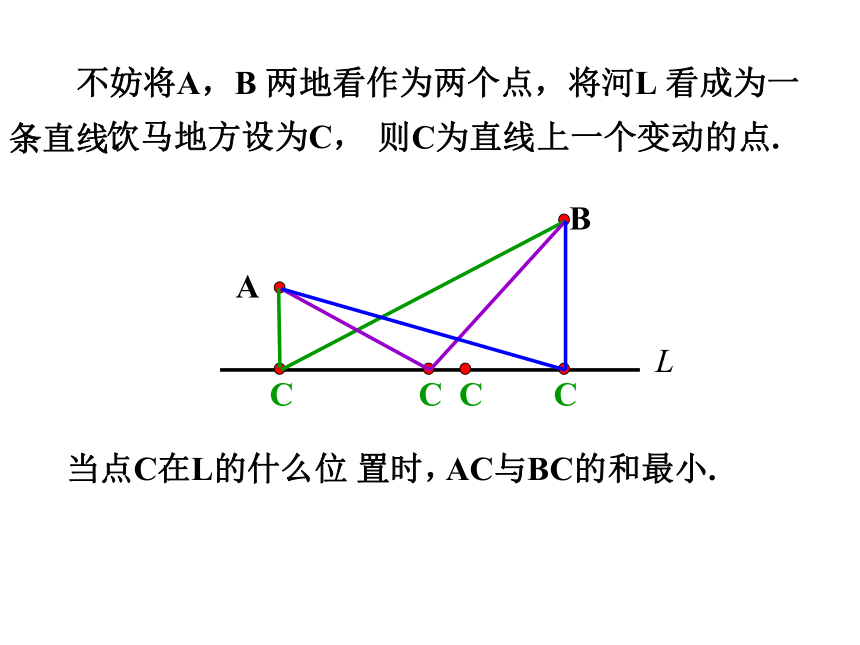
不妨将A,B 两地看作为两个点,将河L 看成为一条直线.
饮马地方设为C,
则C为直线上一个变动的点.
当点C在L的什么位 置时,
AC与BC的和最小.
C
C
C
C
AC与BC的和最小.
C
B
A
L
C
C
A
L
B
当点A与点B在L的两侧时,
点C在L的位置是容易求得的.
连接AB,
设AB与直线L的交点为C.
点C就是所求的点.
理由:
两点之间,线段最短.
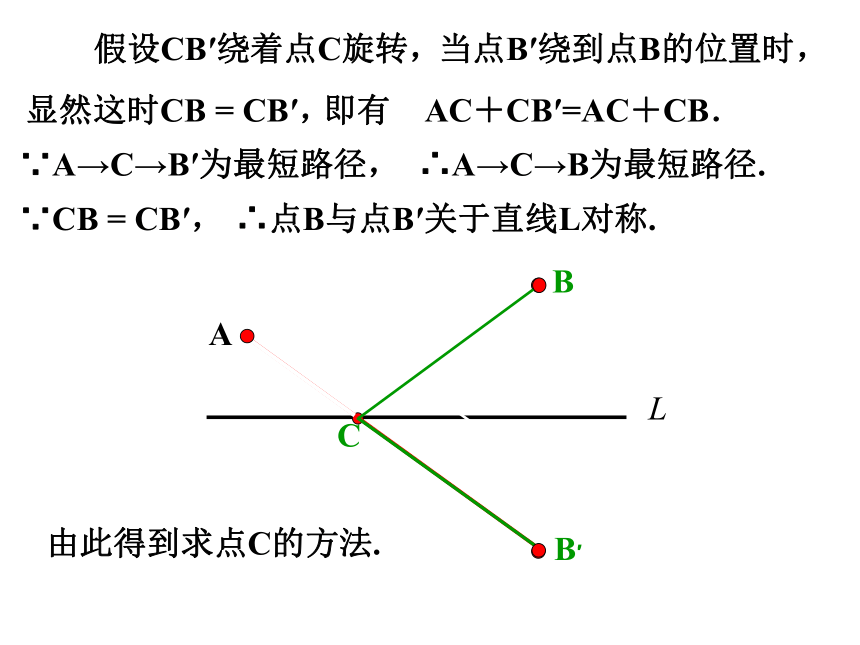
假设CB′绕着点C旋转,
B
C
A
L
B′
当点B′绕到点B的位置时,
显然这时CB = CB′,
即有 AC+CB′=AC+CB.
∵A→C→B′为最短路径,
∴A→C→B为最短路径.
∵CB = CB′,
∴点B与点B′关于直线L对称.
由此得到求点C的方法.
B
A
L
B′
C
画法:
1.画点B关于直线L的对称点B′.
2.连接AB′,
设AB′与直线L的交点为C.
点C就是所求的点.
即AC+BC的值最小.
B
A
L
B′
C
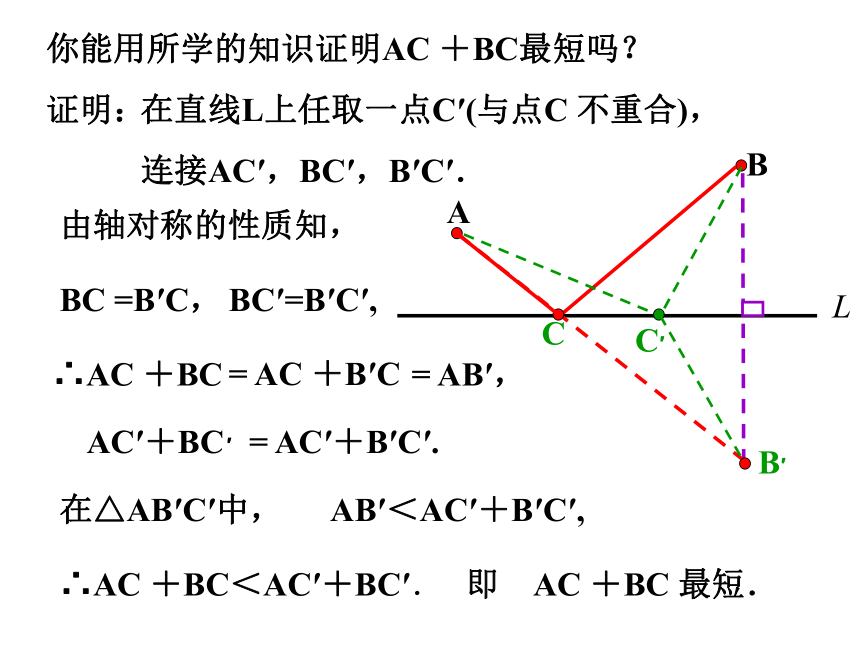
你能用所学的知识证明AC +BC最短吗?
在直线L上任取一点C′(与点C 不重合),
证明:
连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,
BC′=B′C′,
∴AC +BC
= AC +B′C
AC′+BC′
= AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴AC +BC<AC′+BC′.
即 AC +BC 最短.
C′
= AB′,
A
B
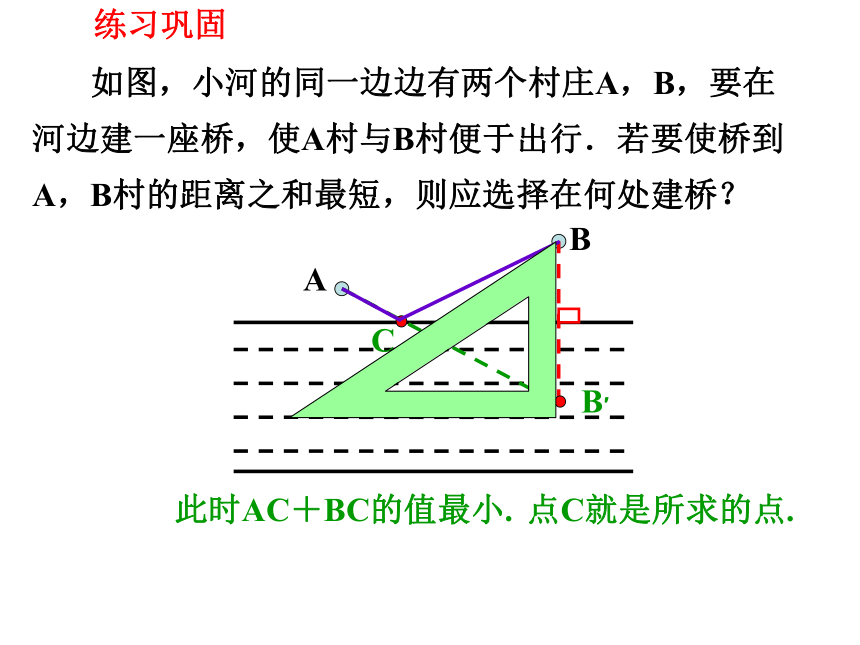
如图,小河的同一边边有两个村庄A,B,要在河边建一座桥,使A村与B村便于出行.若要使桥到A,B村的距离之和最短,则应选择在何处建桥?
B′
C
点C就是所求的点.
此时AC+BC的值最小.
练习巩固
A
B
一条直线上的动点到这条直线同侧的
两点距离之和最小问题:
通常作出其中一定点的对称点;然后利用
“两点之间线段最短”连接对称点和另一定点
连线与对称轴的交点就是动点的位置.
B′
A′
M
例 如图,从A地到B地经过一条小河(河岸平行),
今要在河上建一座与两岸垂直的桥,应如何选择桥
的位置才能使从A地到B地的路程最短?
B
A
探究新知
B
A
设MN是桥所在的位置.
M
N
则从A到B要走的路线是
A→M→N→B.
因为桥长MN是个定值,
所以要使路程AM+MN+NB最短,
只要AM+NB最短即可.
A
N
A
M
要AM+NB最短.
B
B
不妨设想两河岸合并在一起,
此时M与N重合,
若A、N、B刚好在同一条直线上,
则AN+NB最短.
而点A则向下平移了河宽的距离.
B
A
D
C
N
M
(2)连接BC与河岸的一边交于点N.
(3)过点N作河岸的垂线交另一条河岸于点M.
则MN为所建的桥的位置.
解:(1)过点A作AD垂直于河岸,
截AC的长等于河宽.
B
A
M
N
C
N′
M′
∵AM=CN,
AM′=CN′,
AC=MN=M′N′,
∴AM+MN+NB=CN+AC+NB
=MN+CB,
AM′+M′N′+N′B = CN′+AC+N′B
= MN+CN′+N′B
∵CB<
CN′+N′B,
∴MN+CB
<
MN+CN′+N′B;
∴AM+MN+NB
<
AM′+M′N′+N′B.
B
A
M
N
C
N″
M″
∵AM=CN,
AM″=CN″,
AC=MN=M″N″,
∴AM+MN+NB=CN+AC+NB
=MN+CB,
AM″+M″N″+N″B = CN″+AC+N″B
= MN+CN″+N″B,
∵CB<
CN″+N″B,
∴MN+CB
<
MN+CN″+N″B;
∴AM+MN+NB
<
AM″+M″N″+N″B.
B
A
M
N
C
N′
M′
N″
M″
AM+MN+NB
<
AM′+M′N′+N′B.
AM+MN+NB
<
AM″+M″N″+N″B.
1.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是___点.
M
N
A
B
C
D
D
巩固提高
2.如图,在平面直角坐标系中, △ABC的顶点坐标为A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.在y轴上找一点Q,使QC+QB
的和最短.
2
x
y
O
1
2
2
-4
1
-1
-1
A
B
C
Q
D
3.如图,OA、OB是两条公路,在两条公路夹角的内部有一油库M。现在想在两公路上分别建一个加油站,为使运油的的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短。问两加油站应如何选址?
O
A
B
M
E
F
D
C
如图所示,E、F为两个加油站的位置.
解:
4.如图,已知∠AOB=30°,点P为∠ AOB内任意一点,且OP=10,点D和点E分别是射线OA和射线OB上的动点,则△PDE的最小值为 .
A
B
O
P
M
N
D
E
10
△OMN为等边三角形
今天作业
课本P93页第10、11、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.4 最短路径问题
人教版 八年级上册
由一个平面图形可以得到与它关于一条直线对称
的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于对称轴 的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
轴对称的性质
复习旧知
问题 牧马人从图中的A 地出发,到一条笔直的河边L 饮马,然后到B 地.到河边什么地方饮马,可使他所走的路线全程最短?
B
A
L
你能将这个问题转化为数学问题吗?
学习新知
B
A
L
不妨将A,B 两地看作为两个点,将河L 看成为一条直线.
饮马地方设为C,
则C为直线上一个变动的点.
当点C在L的什么位 置时,
AC与BC的和最小.
C
C
C
C
AC与BC的和最小.
C
B
A
L
C
C
A
L
B
当点A与点B在L的两侧时,
点C在L的位置是容易求得的.
连接AB,
设AB与直线L的交点为C.
点C就是所求的点.
理由:
两点之间,线段最短.
假设CB′绕着点C旋转,
B
C
A
L
B′
当点B′绕到点B的位置时,
显然这时CB = CB′,
即有 AC+CB′=AC+CB.
∵A→C→B′为最短路径,
∴A→C→B为最短路径.
∵CB = CB′,
∴点B与点B′关于直线L对称.
由此得到求点C的方法.
B
A
L
B′
C
画法:
1.画点B关于直线L的对称点B′.
2.连接AB′,
设AB′与直线L的交点为C.
点C就是所求的点.
即AC+BC的值最小.
B
A
L
B′
C
你能用所学的知识证明AC +BC最短吗?
在直线L上任取一点C′(与点C 不重合),
证明:
连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,
BC′=B′C′,
∴AC +BC
= AC +B′C
AC′+BC′
= AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴AC +BC<AC′+BC′.
即 AC +BC 最短.
C′
= AB′,
A
B
如图,小河的同一边边有两个村庄A,B,要在河边建一座桥,使A村与B村便于出行.若要使桥到A,B村的距离之和最短,则应选择在何处建桥?
B′
C
点C就是所求的点.
此时AC+BC的值最小.
练习巩固
A
B
一条直线上的动点到这条直线同侧的
两点距离之和最小问题:
通常作出其中一定点的对称点;然后利用
“两点之间线段最短”连接对称点和另一定点
连线与对称轴的交点就是动点的位置.
B′
A′
M
例 如图,从A地到B地经过一条小河(河岸平行),
今要在河上建一座与两岸垂直的桥,应如何选择桥
的位置才能使从A地到B地的路程最短?
B
A
探究新知
B
A
设MN是桥所在的位置.
M
N
则从A到B要走的路线是
A→M→N→B.
因为桥长MN是个定值,
所以要使路程AM+MN+NB最短,
只要AM+NB最短即可.
A
N
A
M
要AM+NB最短.
B
B
不妨设想两河岸合并在一起,
此时M与N重合,
若A、N、B刚好在同一条直线上,
则AN+NB最短.
而点A则向下平移了河宽的距离.
B
A
D
C
N
M
(2)连接BC与河岸的一边交于点N.
(3)过点N作河岸的垂线交另一条河岸于点M.
则MN为所建的桥的位置.
解:(1)过点A作AD垂直于河岸,
截AC的长等于河宽.
B
A
M
N
C
N′
M′
∵AM=CN,
AM′=CN′,
AC=MN=M′N′,
∴AM+MN+NB=CN+AC+NB
=MN+CB,
AM′+M′N′+N′B = CN′+AC+N′B
= MN+CN′+N′B
∵CB<
CN′+N′B,
∴MN+CB
<
MN+CN′+N′B;
∴AM+MN+NB
<
AM′+M′N′+N′B.
B
A
M
N
C
N″
M″
∵AM=CN,
AM″=CN″,
AC=MN=M″N″,
∴AM+MN+NB=CN+AC+NB
=MN+CB,
AM″+M″N″+N″B = CN″+AC+N″B
= MN+CN″+N″B,
∵CB<
CN″+N″B,
∴MN+CB
<
MN+CN″+N″B;
∴AM+MN+NB
<
AM″+M″N″+N″B.
B
A
M
N
C
N′
M′
N″
M″
AM+MN+NB
<
AM′+M′N′+N′B.
AM+MN+NB
<
AM″+M″N″+N″B.
1.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是___点.
M
N
A
B
C
D
D
巩固提高
2.如图,在平面直角坐标系中, △ABC的顶点坐标为A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.在y轴上找一点Q,使QC+QB
的和最短.
2
x
y
O
1
2
2
-4
1
-1
-1
A
B
C
Q
D
3.如图,OA、OB是两条公路,在两条公路夹角的内部有一油库M。现在想在两公路上分别建一个加油站,为使运油的的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短。问两加油站应如何选址?
O
A
B
M
E
F
D
C
如图所示,E、F为两个加油站的位置.
解:
4.如图,已知∠AOB=30°,点P为∠ AOB内任意一点,且OP=10,点D和点E分别是射线OA和射线OB上的动点,则△PDE的最小值为 .
A
B
O
P
M
N
D
E
10
△OMN为等边三角形
今天作业
课本P93页第10、11、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
