3.1.2成比例线段 课件(共29张PPT)
文档属性
| 名称 | 3.1.2成比例线段 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
3.1.2 成比例线段
湘教版九年级上册
教学目标
1. 理解和掌握线段的比,成比例线段的概念.
2. 能够判断四条线段是否比例线段.
3. 理解黄金分割的概念,掌握黄金分割比的比值.
4. 了解现实生活中的黄金分割比,体验数学与生活的联系.
1. 由比例 可以得出的式子是( )
A. B.
C. D.
温故知新
2. 求下列各式中x的值.
(1) 7∶x =0.14 ∶8; (2) ∶ = ∶x.
C
新知导入
3. 比例的基本性质是什么?
4. 把一个比例式变形为另一个比例式的依据有哪些?
如果a∶b=c∶d 或 ,那么ad=bc.
即比例的两外项之积等于两内项之积(内外项分别乘、交叉乘).
①比例的基本性质;② 等式的性质.
新知讲解
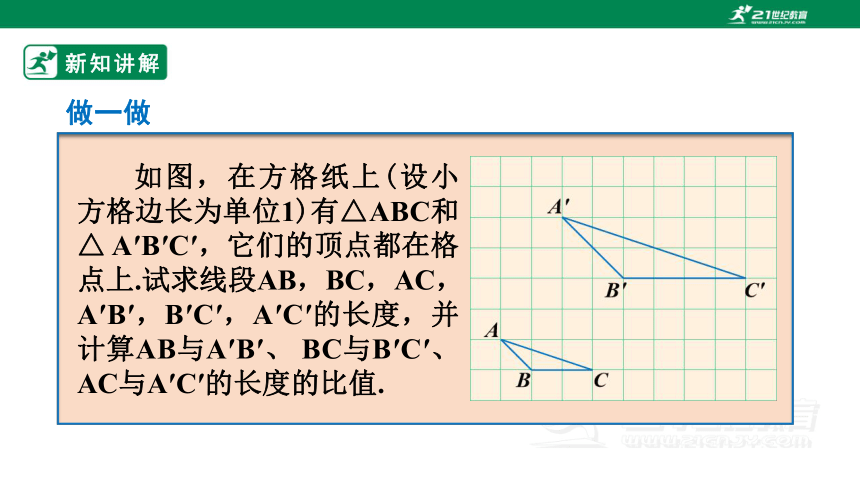
如图,在方格纸上(设小方格边长为单位1)有△ABC和△ A′B′C′,它们的顶点都在格点上.试求线段AB,BC,AC, A′B′,B′C′,A′C′的长度,并计算AB与A′B′、 BC与B′C′、AC与A′C′的长度的比值.
做一做
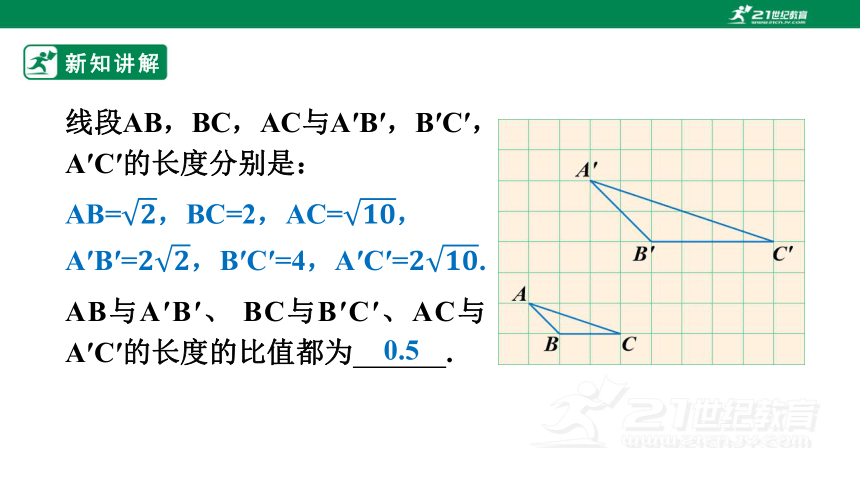
新知讲解
A′B′=,B′C′=4,A′C′=.
AB=,BC=2,AC=,
线段AB,BC,AC与A′B′,B′C′,A′C′的长度分别是:
AB与A′B′、 BC与B′C′、AC与A′C′的长度的比值都为 .
0.5
新知讲解
一般地,如果选用同一长度量得两条线段AB, A′B′的长度分别为m,n,那么把它们的长度的
比叫作这两条线段AB, A′B′的比,记作
, 或 AB∶A′B′=m∶n.
如果的比值为k,那么上式也可以写成
, 或 AB=k·A′B′.
新知讲解
在右图中,对于△ABC和△A′B′C′,有
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫作成比例线段,简称比例线段.
新知讲解
例如,已知四条线段a,b,c,d,若,则a,b,c,d是比例线段.
类似地,如果,那么称线段AB,BC,AC与线段A′B′,B′C′,A′C′对应成比例.
例题教学
例3 已知四条线段a ,b , c, d的长度分别为0.8cm, 2cm, 1.2cm, 3cm ,问a ,b , c, d是比例线段吗?
解
∵
∴
,
即a ,b , c, d是比例线段.
合作探究
古希腊数学家、天文学家欧多克索斯曾经提出一个问题:
能否将一条线段AB分成不相等的两部分,使较短线段BC与较长线段AC的比等于线段AC与原线段AB的比?
即,使得 成立?
C
A
B
合作探究
如果能做到的话,那么称线段AB被点C黄金分割,点C叫作线段AB的黄金分割点,较长线段AC与原线段AB的比叫作黄金分割比.
C
A
B
合作探究
运用一元二次方程,可以求出黄金分割比的数值.
如图,设线段AB的长度为1个单位,点C为线段AB上一点,且AC的长度为x个单位,则CB的长度为(1-x)个单位,根据 ,可列出方程:
C
A
B
合作探究
由于x≠0,因此在方程两边同乘x,得
即
x +x-1=0,
1-x=x ,
解得
x = ,
x = (舍去).
因此,黄金分割比
≈0.618.
合作探究
事实上,我们一定可以把一条线段黄金分割,黄金分
割比为 ,它约等于0.618.
C
A
B
阅读欣赏
视觉生理学的研究成果表明,符合黄金分割的形式很容易使人产生视觉上的美感.许多世界著名古建筑物中,都包含“黄金分割比”,例如古希腊的巴台农神庙、印度泰姬陵、法国巴黎圣母院这些著名建筑的正面的高度与底面宽度之比均约为黄金分割比.
巴台农神庙
泰姬陵
阅读欣赏
在现代,许多建筑的设计也采用了黄金分割,例如上海的东方明珠广播电视塔的上球体就处于整个塔身高度的黄金分割处.
上海东方明珠广播电视塔
阅读欣赏
神奇的“黄金分割比”也出现在许多著名艺术作品中,如在意大利著名画家达·芬奇的名作《蒙拉丽莎》中,人物的脸的宽度与高度的比就是一个黄金分割比.
蒙娜丽莎
课堂练习
1. 下列各组长度的线段(单位:cm)中,成比例线段的是( )
A. 2,3,4,7 B. 1,3,3,6
C. 2,3,6,9 D. 1,5,3,12
C
提示:通过分别计算第1、2条线段的比和第3、4条线段的比,根据比值是否相等,用成比例线段的概念作出判断.
课堂练习
2. 点B是线段AC的黄金分割点,且ABA. B.
C. D.
提示:先画出线段图,再根据黄金分割比的概念和已知列出式子,即可求出BC.
B
课堂练习
3. 若线段a,b,c,d成比例,其中a=3 cm,b=6 cm,c=2 cm,则d的长为( )
A. 1cm B. 2cm
C. 3cm D. 4cm
D
提示:先列出比例式,再运用比例的性质,即可得d的长.
课堂总结
1. 什么叫作两条线段的比?如何表示两条线段的比?
两条线段AB, A′B′的长度m,n的比叫作这两条线段AB, A′B′的比
.
, 或 AB∶A′B′=m∶n.
写成
, 或 AB=k·A′B′
或
(若的比值为k).
课堂总结
2. 什么叫作成比例线段(比例线段)?什么叫作线段对应成比例?
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫作成比例线段,简称比例线段.
在几何图形中,如果两组对应线段的比相等,那么这两组中的线段对应成比例.
课堂总结
3. 什么叫作黄金分割和黄金分割点?什么黄金分割比?黄金分割比的值是多少?
如果一条线段被一个点分成较长和较短的两条线段,且较短线段与较长线段的比等于较长线段与原来线段的比,即较短线段、较长线段、较长线段、原线段成比例,则叫作把原线段黄金分割,这个点叫作黄金分割点.
在黄金分割中,较长线段与原线段的比叫作黄金分割比.
黄金分割比等于≈0.618.
板书设计
成比例线段
两条线段的比的概念及表示方法
成比例线段的概念
对应线段成比例的概念
黄金分割、黄金分割点、黄金分割比
作业布置
第66页课后练习第1、2题
1. 已知a,b,c,d是比例线段.
(1)若a=0.8cm,b=1cm,c=1cm,求d;
(2)若a=12cm,c=3cm,d=15cm,求b;
(3)若a=5cm,b=4cm,d=8cm,求c.
提示:(1)先列比例式0.8∶1=1∶d,再利用比例的基本性质即可求出d=1.25.第(2)(3)题的解法相同.
作业布置
2. 在比例尺1∶1 000 000的地图上,量得A,B两地的距离是25cm.求A,B两地之间的实际距离.
解:设A,B两地之间的实际距离为xcm,根据题意得,
1∶1 000 000=25∶x
即
1·x=1 000 000×25
解得
x=25 000 000.
25 000 000cm=250km.
答:A,B两地之间的实际距离为250km.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.1.2 成比例线段
湘教版九年级上册
教学目标
1. 理解和掌握线段的比,成比例线段的概念.
2. 能够判断四条线段是否比例线段.
3. 理解黄金分割的概念,掌握黄金分割比的比值.
4. 了解现实生活中的黄金分割比,体验数学与生活的联系.
1. 由比例 可以得出的式子是( )
A. B.
C. D.
温故知新
2. 求下列各式中x的值.
(1) 7∶x =0.14 ∶8; (2) ∶ = ∶x.
C
新知导入
3. 比例的基本性质是什么?
4. 把一个比例式变形为另一个比例式的依据有哪些?
如果a∶b=c∶d 或 ,那么ad=bc.
即比例的两外项之积等于两内项之积(内外项分别乘、交叉乘).
①比例的基本性质;② 等式的性质.
新知讲解
如图,在方格纸上(设小方格边长为单位1)有△ABC和△ A′B′C′,它们的顶点都在格点上.试求线段AB,BC,AC, A′B′,B′C′,A′C′的长度,并计算AB与A′B′、 BC与B′C′、AC与A′C′的长度的比值.
做一做
新知讲解
A′B′=,B′C′=4,A′C′=.
AB=,BC=2,AC=,
线段AB,BC,AC与A′B′,B′C′,A′C′的长度分别是:
AB与A′B′、 BC与B′C′、AC与A′C′的长度的比值都为 .
0.5
新知讲解
一般地,如果选用同一长度量得两条线段AB, A′B′的长度分别为m,n,那么把它们的长度的
比叫作这两条线段AB, A′B′的比,记作
, 或 AB∶A′B′=m∶n.
如果的比值为k,那么上式也可以写成
, 或 AB=k·A′B′.
新知讲解
在右图中,对于△ABC和△A′B′C′,有
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫作成比例线段,简称比例线段.
新知讲解
例如,已知四条线段a,b,c,d,若,则a,b,c,d是比例线段.
类似地,如果,那么称线段AB,BC,AC与线段A′B′,B′C′,A′C′对应成比例.
例题教学
例3 已知四条线段a ,b , c, d的长度分别为0.8cm, 2cm, 1.2cm, 3cm ,问a ,b , c, d是比例线段吗?
解
∵
∴
,
即a ,b , c, d是比例线段.
合作探究
古希腊数学家、天文学家欧多克索斯曾经提出一个问题:
能否将一条线段AB分成不相等的两部分,使较短线段BC与较长线段AC的比等于线段AC与原线段AB的比?
即,使得 成立?
C
A
B
合作探究
如果能做到的话,那么称线段AB被点C黄金分割,点C叫作线段AB的黄金分割点,较长线段AC与原线段AB的比叫作黄金分割比.
C
A
B
合作探究
运用一元二次方程,可以求出黄金分割比的数值.
如图,设线段AB的长度为1个单位,点C为线段AB上一点,且AC的长度为x个单位,则CB的长度为(1-x)个单位,根据 ,可列出方程:
C
A
B
合作探究
由于x≠0,因此在方程两边同乘x,得
即
x +x-1=0,
1-x=x ,
解得
x = ,
x = (舍去).
因此,黄金分割比
≈0.618.
合作探究
事实上,我们一定可以把一条线段黄金分割,黄金分
割比为 ,它约等于0.618.
C
A
B
阅读欣赏
视觉生理学的研究成果表明,符合黄金分割的形式很容易使人产生视觉上的美感.许多世界著名古建筑物中,都包含“黄金分割比”,例如古希腊的巴台农神庙、印度泰姬陵、法国巴黎圣母院这些著名建筑的正面的高度与底面宽度之比均约为黄金分割比.
巴台农神庙
泰姬陵
阅读欣赏
在现代,许多建筑的设计也采用了黄金分割,例如上海的东方明珠广播电视塔的上球体就处于整个塔身高度的黄金分割处.
上海东方明珠广播电视塔
阅读欣赏
神奇的“黄金分割比”也出现在许多著名艺术作品中,如在意大利著名画家达·芬奇的名作《蒙拉丽莎》中,人物的脸的宽度与高度的比就是一个黄金分割比.
蒙娜丽莎
课堂练习
1. 下列各组长度的线段(单位:cm)中,成比例线段的是( )
A. 2,3,4,7 B. 1,3,3,6
C. 2,3,6,9 D. 1,5,3,12
C
提示:通过分别计算第1、2条线段的比和第3、4条线段的比,根据比值是否相等,用成比例线段的概念作出判断.
课堂练习
2. 点B是线段AC的黄金分割点,且AB
C. D.
提示:先画出线段图,再根据黄金分割比的概念和已知列出式子,即可求出BC.
B
课堂练习
3. 若线段a,b,c,d成比例,其中a=3 cm,b=6 cm,c=2 cm,则d的长为( )
A. 1cm B. 2cm
C. 3cm D. 4cm
D
提示:先列出比例式,再运用比例的性质,即可得d的长.
课堂总结
1. 什么叫作两条线段的比?如何表示两条线段的比?
两条线段AB, A′B′的长度m,n的比叫作这两条线段AB, A′B′的比
.
, 或 AB∶A′B′=m∶n.
写成
, 或 AB=k·A′B′
或
(若的比值为k).
课堂总结
2. 什么叫作成比例线段(比例线段)?什么叫作线段对应成比例?
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫作成比例线段,简称比例线段.
在几何图形中,如果两组对应线段的比相等,那么这两组中的线段对应成比例.
课堂总结
3. 什么叫作黄金分割和黄金分割点?什么黄金分割比?黄金分割比的值是多少?
如果一条线段被一个点分成较长和较短的两条线段,且较短线段与较长线段的比等于较长线段与原来线段的比,即较短线段、较长线段、较长线段、原线段成比例,则叫作把原线段黄金分割,这个点叫作黄金分割点.
在黄金分割中,较长线段与原线段的比叫作黄金分割比.
黄金分割比等于≈0.618.
板书设计
成比例线段
两条线段的比的概念及表示方法
成比例线段的概念
对应线段成比例的概念
黄金分割、黄金分割点、黄金分割比
作业布置
第66页课后练习第1、2题
1. 已知a,b,c,d是比例线段.
(1)若a=0.8cm,b=1cm,c=1cm,求d;
(2)若a=12cm,c=3cm,d=15cm,求b;
(3)若a=5cm,b=4cm,d=8cm,求c.
提示:(1)先列比例式0.8∶1=1∶d,再利用比例的基本性质即可求出d=1.25.第(2)(3)题的解法相同.
作业布置
2. 在比例尺1∶1 000 000的地图上,量得A,B两地的距离是25cm.求A,B两地之间的实际距离.
解:设A,B两地之间的实际距离为xcm,根据题意得,
1∶1 000 000=25∶x
即
1·x=1 000 000×25
解得
x=25 000 000.
25 000 000cm=250km.
答:A,B两地之间的实际距离为250km.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
