3.2 平行线分线段成比例 教学设计

中小学教育资源及组卷应用平台
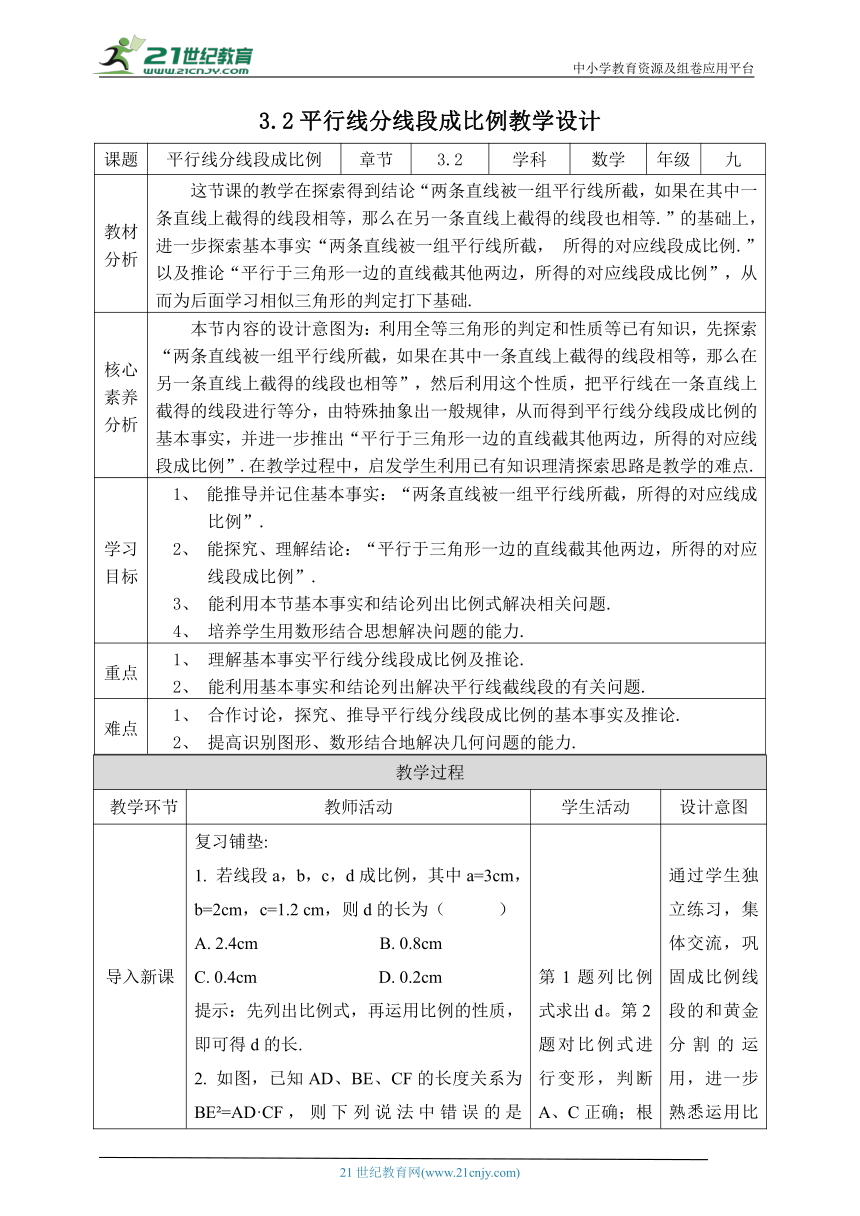
3.2平行线分线段成比例教学设计
课题 平行线分线段成比例 章节 3.2 学科 数学 年级 九
教材分析 这节课的教学在探索得到结论“两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.”的基础上，进一步探索基本事实“两条直线被一组平行线所截， 所得的对应线段成比例.”以及推论“平行于三角形一边的直线截其他两边，所得的对应线段成比例”，从而为后面学习相似三角形的判定打下基础.
核心素养分析 本节内容的设计意图为：利用全等三角形的判定和性质等已有知识，先探索“两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等”，然后利用这个性质，把平行线在一条直线上截得的线段进行等分，由特殊抽象出一般规律，从而得到平行线分线段成比例的基本事实，并进一步推出“平行于三角形一边的直线截其他两边，所得的对应线段成比例”.在教学过程中，启发学生利用已有知识理清探索思路是教学的难点.
学习目标 1、 能推导并记住基本事实：“两条直线被一组平行线所截，所得的对应线成比例”.2、 能探究、理解结论：“平行于三角形一边的直线截其他两边，所得的对应线段成比例”. 3、 能利用本节基本事实和结论列出比例式解决相关问题.4、 培养学生用数形结合思想解决问题的能力.
重点 1、 理解基本事实平行线分线段成比例及推论.2、 能利用基本事实和结论列出解决平行线截线段的有关问题.
难点 1、 合作讨论，探究、推导平行线分线段成比例的基本事实及推论.2、 提高识别图形、数形结合地解决几何问题的能力.
教学过程
教学环节 教师活动 学生活动 设计意图
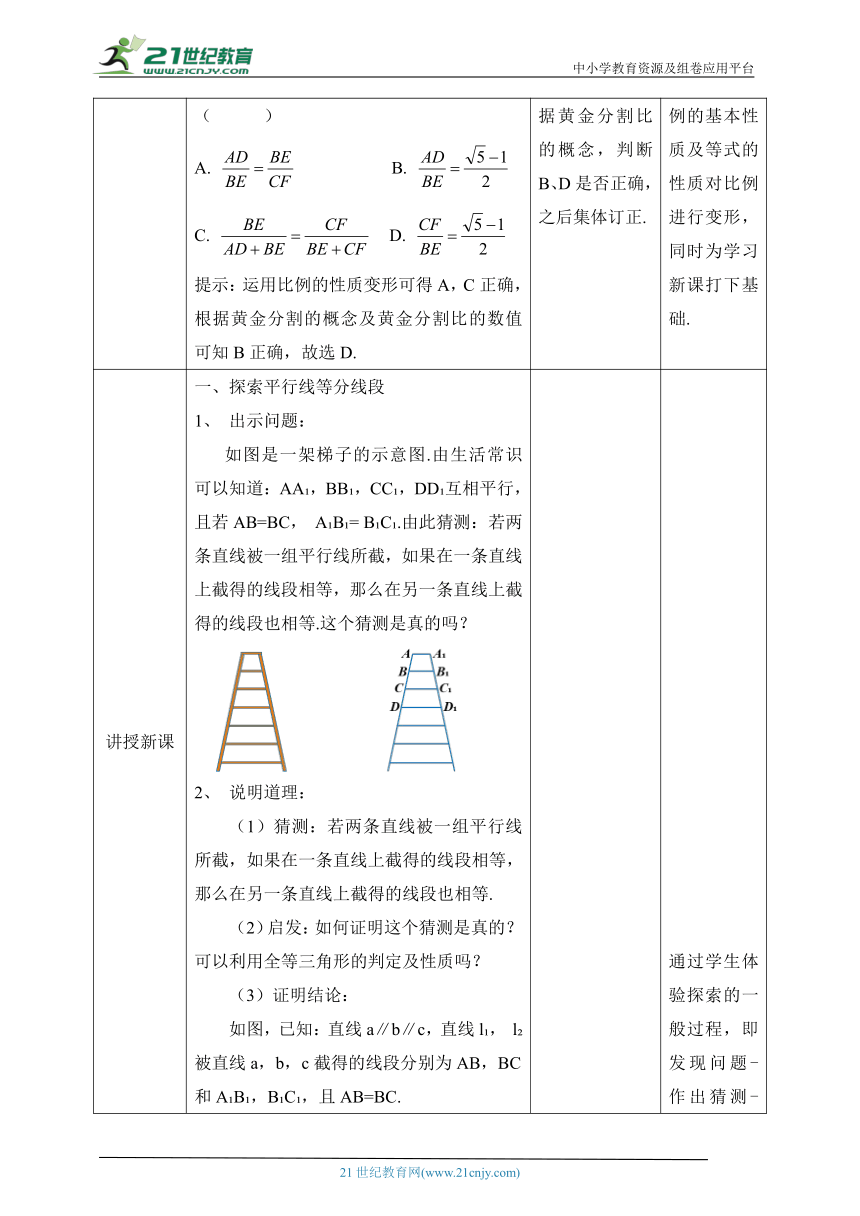
导入新课 复习铺垫:1. 若线段a，b，c，d成比例，其中a=3cm，b=2cm，c=1.2 cm，则d的长为（ ）A. 2.4cm B. 0.8cmC. 0.4cm D. 0.2cm提示：先列出比例式，再运用比例的性质，即可得d的长.2. 如图，已知AD、BE、CF的长度关系为BE =AD·CF，则下列说法中错误的是（ ）A. B. C. D. 提示：运用比例的性质变形可得A，C正确，根据黄金分割的概念及黄金分割比的数值可知B正确，故选D. 第1题列比例式求出d。第2题对比例式进行变形，判断A、C正确；根据黄金分割比的概念，判断B、D是否正确，之后集体订正. 通过学生独立练习，集体交流，巩固成比例线段的和黄金分割的运用，进一步熟悉运用比例的基本性质及等式的性质对比例进行变形，同时为学习新课打下基础.
讲授新课 一、探索平行线等分线段1、 出示问题：如图是一架梯子的示意图.由生活常识可以知道：AA ，BB ，CC ，DD 互相平行，且若AB=BC， A B = B C .由此猜测：若两条直线被一组平行线所截，如果在一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.这个猜测是真的吗？ 2、 说明道理：（1）猜测：若两条直线被一组平行线所截，如果在一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.（2）启发：如何证明这个猜测是真的？可以利用全等三角形的判定及性质吗？（3）证明结论：如图，已知：直线a∥b∥c，直线l ， l 被直线a，b，c截得的线段分别为AB，BC和A B ，B C ，且AB=BC. 求证： A B =B C . 过点B作直线 l ∥ l ，分别与直线交于点A ，C . 由于a∥b∥c， l ∥ l ，因此由“夹在两平行线间的平行线段相等”可知，A B=A B ，BC =B C .在△BAA 和△BCC 中，∠ABA =∠CBC ，BA=BC， ∠BAA = ∠BCC . 因此，△BAA ≌△BCC .从而 BA =BC .所以，A B =B C . 3、 归纳、展示结论由此可以得到：两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.二、探索平行线分线段成比例1、 出示问题：如图，任意画两条直线l ，l ，再画三条与l ，l 相交的平行直线a，b，c.分别度量被直线l ，l 截得的线段AB，BC，A B ，B C 的长度. 与相等吗？任意平移直线c，再度量AB，BC，A B ，B C 的长度，与还相等吗 2、 说明道理：（1）猜测：=.（2）启发：如何证明这个猜测是真的？思路：将线段AB，BC分成长度相等的几段，利用平行线等分线段的结论证明.先证明当=时，=.再证明当=时，=.（3）证明结论：①假设=，则把线段AB二等分，分点为D，过点D作直线d∥a，交l 于点D ；把线段BC三等分，三等分点为E，F，分别过点E，F作直线e∥a， f∥a，交l 于点E ，F ，如图. 由已知 =，得 AB=BC.由于 AD=DB=AB，BE=EF=FC=BC，因此 AD=DB=BE=EF=FC.由于 a∥d∥b∥e∥f ∥c，所以 A D =D B =B E =E F = F C .从而 ==，即 =.②类似地，可以证明：直线a∥b∥c，直线l ，l 被直线a，b，c截得的线段分别为AB，BC和A B ，B C ，若 = (其中m，n是是正整数)，则 =. 进一步可以证明：若=k (其中k为无理数)，则 =k. =.③运用比例的性质，我们还可以得到=，=，=.3、 归纳、展示结论由此，得到以下基本事实：两条直线被一组平行线所截， 所得的对应线段成比例.我们把以上基本事实简称为平行线分线段成比例.三、探索平行线分线段成比例的推论1、 出示问题：如图，在△ABC中，已知DE∥BC，则和成立吗？为什么？ 2、 说明道理：如图，过点A作直线MN，使MN∥DE.∵ MN∥BC，∴ MN∥DE∥BC.因此AB，AC被一组平行线MN，DE，BC所截，则由平行线分线段成比例可得，，.同时还可以得到，. 3、 归纳、展示结论平行于三角形一边的直线截其他两边， 所得的对应线段成比例.四、教学例题例 如图，已知AA ∥BB ∥CC ，AB=2，BC=3，A B =1.5，求B C 的长. 解 由平行线分线段成比例可知，∵ =，即，∴ B C ==2.25. 先通过观察，作出猜测；再合作讨论，理清说理思路；然后通过证明过程，归纳记住结论..在教师引导下，学生通过合作，探究基本事实“两条直线被一组平行线所截，所得的对应线段成比例”.先由学生通过度量、计算，作出猜测，再通过讨论，得出证明思路，说出证明过程及理由.最后概括出基本事实，并记忆掌握.学生作出辅助线，阅读图文，完成证明.通过交流，得出结论.学生根据题意，说出要列出的比例式，并进行计算. 通过学生体验探索的一般过程，即发现问题-作出猜测-证明猜测-归纳结论，培养学生学会探究几何结论的一般步骤，启发学生思维，培养解决几何问题的能力，从而提高获取新知的能力. 通过教师启发，学生操作、首脑并用，学生获取这个基本事实的内容，通过教师讲解、ppt展示，学生理解基本事实的形成过程—由特殊认知到一般的理性认知，从而帮助学生全面准确地理解平行线分线段成比例的基本事实.通过学生独立探索，培养学生看图联想、逻辑推理能力.通过学习例题，巩固所学基本事实：平行线分线段成比例.并学会运用.
课堂练习 当堂练习：1、 如图，已知l ∥l ∥l ，AG=4，GB=2，BC=10，则的值为（ ）A. B. 2C. D. 【答案】D【提示】由AG=4，GB=2，得AB=6.再根据平行线分线段成比例，即得答案D.2、 (邛崃市期末)如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC.若AD∶AB=3∶4，AE=9，则AC等于（ ） A. 6 B. 8C. 10 D. 12 【答案】D【提示】运用平行线分线段对应成比例解决问题，一定要找出对应线段，并根据对应线段列出比例式.书面练习：第71页课后练习第1、2题.（见配套课件） 运用概念，通过计算，做出判断，选择答案.交流合作，纠错纠偏.独立练习，强化能力. 通过练习，巩固所学结论、基本事实和推论，提高知识应用能力，防范错误认知，提高合作能力.
课堂小结 这节课我们学过的基本事实或结论有哪些？请说一说.PPT：①两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.②两条直线被一组平行线所截， 所得的对应线段成比例(基本事实).③平行于三角形一边的直线截其他两边， 所得的对应线段成比例. 回顾、交流、整理本节课所学内容。 巩固知识要点，梳理知识网络.
板书
课后反思
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)