3.2 平行线分线段成比例 课件(共26张PPT)
文档属性
| 名称 | 3.2 平行线分线段成比例 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 20:52:14 | ||
图片预览







文档简介
(共26张PPT)
3.2 平行线分线段成比例
湘教版九年级上册
教学目标
1. 能推导并记住基本事实:“两条直线被一组平行线所截,
所得的对应线段成比例”.
2. 能探究、理解结论:“平行于三角形一边的直线截其他两
边,所得的对应线段成比例”.
3. 能利用本节基本事实和结论列出比例式解决相关问题.
4. 培养学生用数形结合思想解决问题的能力.
温故知新
1. 若线段a,b,c,d成比例,其中a=3cm,b=2cm,c=1.2 cm,则d的长为( )
A. 2.4cm B. 0.8cm
C. 0.4cm D. 0.2cm
D
提示:先列出比例式,再运用比例的性质,即可得d的长.
新知导入
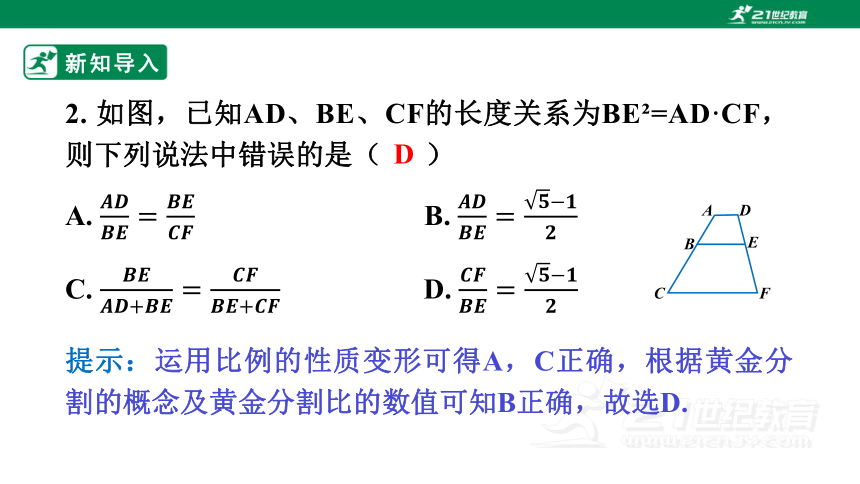
2. 如图,已知AD、BE、CF的长度关系为BE =AD·CF,则下列说法中错误的是( )
A. B.
C. D.
A
B
C
D
E
F
D
提示:运用比例的性质变形可得A,C正确,根据黄金分割的概念及黄金分割比的数值可知B正确,故选D.
新知讲解
如图是一架梯子的示意图.由生活常识可以知道:AA ,BB ,CC ,DD 互相平行,且若AB=BC, A B = B C .由此猜测:若两条直线被一组平行线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.这个猜测是真的吗?
观察
A
C
D
B
D
A
B
C
新知讲解
如图,已知:直线a∥b∥c,直线l , l 被直线a,b,c截得的线段分别为AB,BC和A B ,B C ,且AB=BC. 求证: A B =B C .
过点B作直线 l ∥ l ,分别与直线交于点A ,C . 由于a∥b∥c, l ∥ l ,因此由“夹在两平行线间的平行线段相等”可知,
A B=A B , BC =B C .
a
b
c
l
l
A
B
C
A
B
C
A
C
l
新知讲解
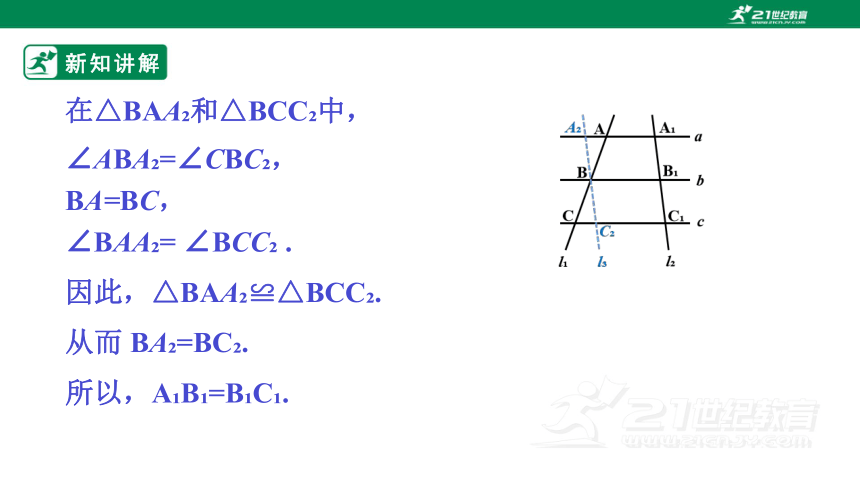
在△BAA 和△BCC 中,
∠ABA =∠CBC ,
BA=BC,
∠BAA = ∠BCC .
因此,△BAA ≌△BCC .
从而 BA =BC .
所以,A B =B C .
新知讲解
由此可以得到:
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
新知讲解
如图,任意画两条直线l ,l ,再画三条与l ,l 相交的平行直线a,b,c.分别度量被直线l ,l 截得的线段AB,BC,A B ,B C 的长度. 与相等吗?任意平移直线c,再度量AB,BC,A B ,B C 的长度,与还相等吗
动脑筋
a
b
c
l
l
A
B
C
A
B
C
新知讲解
我们可以利用已有结论:“两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.”来证明结论:
.
新知讲解
首先我们证明:当 时,.
当 时,则把线段AB二等分,分点为D,过点D作直线d∥a,交l 于点D ;把线段BC三等分,三等分点为E,F,分别过点E,F作直线e∥a, f∥a,交l 于点E ,F ,如图
.
d
D
a
b
c
l
l
A
B
C
A
B
C
E
D
E
F
F
e
f
新知讲解
由已知 ,得 .
d
D
a
b
c
l
l
A
B
C
A
B
C
E
D
E
F
F
e
f
由于 AD=DB= ,BE=EF=FC,
因此 AD=DB=BE=EF=FC.
由于 a∥d∥b∥e∥f ∥c,
所以 A D =D B =B E =E F = F C .
从而 = ,
即 .
新知讲解
类似地,可以证明:直线a∥b∥c,直线l ,l 被直线a,b,c截得的线段分别为AB,BC和A B ,B C ,若 (其中m,n是是正整数),则 . 进一步可以证明:若 (其中k为无理数),则 .
a
b
c
l
l
A
B
C
A
B
C
从而
.
新知讲解
运用比例的性质,我们还可以得到
a
b
c
l
l
A
B
C
A
B
C
,
,
.
由此,得到以下基本事实:
两条直线被一组平行线所截, 所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
新知讲解
如图,在△ABC中,已知DE∥BC,则
和 成立吗?为什么?
动脑筋
A
B
C
D
E
新知讲解
如图,过点A作直线MN,使MN∥DE.
∵ MN∥BC,
∴ MN∥DE∥BC.
因此AB,AC被一组平行线MN,DE,BC所截,则由平行线分线段成比例可得,
,
.
同时还可以得到
,
.
A
B
C
D
E
M
N
新知讲解
由此,得到以下结论:
平行于三角形一边的直线截其他两边, 所得的对应线段成比例.
A
B
C
D
E
例题教学
例 如图,已知AA ∥BB ∥CC ,AB=2,BC=3,A B =1.5,求B C 的长.
解 由平行线分线段成比例可知,
因此
.
A
A
B
C
C
B
即
课堂练习
1. 如图,已知l ∥l ∥l ,AG=4,GB=2,BC=10,则的值为( )
A. B. 2
C. D.
D
l
l
A
E
F
D
C
B
l
G
提示:由AG=4,GB=2,得AB=6.再根据平行线分线段成比例,即得
课堂练习
2. (邛崃市期末)如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.若AD∶AB=3∶4,AE=9,则AC等于( )
A. 6 B. 8
C. 10 D. 12
提示:运用平行线分线段对应成比例解决问题,一定要找出对应线段,并根据对应线段列出比例式.
D
A
B
C
D
E
课堂总结
这节课我们学过的基本事实或结论有哪些?请说一说.
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
两条直线被一组平行线所截, 所得的对应线段成比例(基本事实).
平行于三角形一边的直线截其他两边, 所得的对应线段成比例.
板书设计
平行线分线段成比例
平行线等分线段
平行线分线段成比例
平行于三角形一边的直线截另两边对应线段成比例.
作业布置
第71页课后练习第1、2题
1.如图, AC,BD相交于点O,直线MN过点O,且BA∥MN∥CD.已知OA=3,OB=1,OD=2,求OC的长.
A
B
O
M
N
D
C
作业布置
2.如图, 点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AB=3,AD=2,EC=1.8,求AC的长.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2 平行线分线段成比例
湘教版九年级上册
教学目标
1. 能推导并记住基本事实:“两条直线被一组平行线所截,
所得的对应线段成比例”.
2. 能探究、理解结论:“平行于三角形一边的直线截其他两
边,所得的对应线段成比例”.
3. 能利用本节基本事实和结论列出比例式解决相关问题.
4. 培养学生用数形结合思想解决问题的能力.
温故知新
1. 若线段a,b,c,d成比例,其中a=3cm,b=2cm,c=1.2 cm,则d的长为( )
A. 2.4cm B. 0.8cm
C. 0.4cm D. 0.2cm
D
提示:先列出比例式,再运用比例的性质,即可得d的长.
新知导入
2. 如图,已知AD、BE、CF的长度关系为BE =AD·CF,则下列说法中错误的是( )
A. B.
C. D.
A
B
C
D
E
F
D
提示:运用比例的性质变形可得A,C正确,根据黄金分割的概念及黄金分割比的数值可知B正确,故选D.
新知讲解
如图是一架梯子的示意图.由生活常识可以知道:AA ,BB ,CC ,DD 互相平行,且若AB=BC, A B = B C .由此猜测:若两条直线被一组平行线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.这个猜测是真的吗?
观察
A
C
D
B
D
A
B
C
新知讲解
如图,已知:直线a∥b∥c,直线l , l 被直线a,b,c截得的线段分别为AB,BC和A B ,B C ,且AB=BC. 求证: A B =B C .
过点B作直线 l ∥ l ,分别与直线交于点A ,C . 由于a∥b∥c, l ∥ l ,因此由“夹在两平行线间的平行线段相等”可知,
A B=A B , BC =B C .
a
b
c
l
l
A
B
C
A
B
C
A
C
l
新知讲解
在△BAA 和△BCC 中,
∠ABA =∠CBC ,
BA=BC,
∠BAA = ∠BCC .
因此,△BAA ≌△BCC .
从而 BA =BC .
所以,A B =B C .
新知讲解
由此可以得到:
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
新知讲解
如图,任意画两条直线l ,l ,再画三条与l ,l 相交的平行直线a,b,c.分别度量被直线l ,l 截得的线段AB,BC,A B ,B C 的长度. 与相等吗?任意平移直线c,再度量AB,BC,A B ,B C 的长度,与还相等吗
动脑筋
a
b
c
l
l
A
B
C
A
B
C
新知讲解
我们可以利用已有结论:“两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.”来证明结论:
.
新知讲解
首先我们证明:当 时,.
当 时,则把线段AB二等分,分点为D,过点D作直线d∥a,交l 于点D ;把线段BC三等分,三等分点为E,F,分别过点E,F作直线e∥a, f∥a,交l 于点E ,F ,如图
.
d
D
a
b
c
l
l
A
B
C
A
B
C
E
D
E
F
F
e
f
新知讲解
由已知 ,得 .
d
D
a
b
c
l
l
A
B
C
A
B
C
E
D
E
F
F
e
f
由于 AD=DB= ,BE=EF=FC,
因此 AD=DB=BE=EF=FC.
由于 a∥d∥b∥e∥f ∥c,
所以 A D =D B =B E =E F = F C .
从而 = ,
即 .
新知讲解
类似地,可以证明:直线a∥b∥c,直线l ,l 被直线a,b,c截得的线段分别为AB,BC和A B ,B C ,若 (其中m,n是是正整数),则 . 进一步可以证明:若 (其中k为无理数),则 .
a
b
c
l
l
A
B
C
A
B
C
从而
.
新知讲解
运用比例的性质,我们还可以得到
a
b
c
l
l
A
B
C
A
B
C
,
,
.
由此,得到以下基本事实:
两条直线被一组平行线所截, 所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
新知讲解
如图,在△ABC中,已知DE∥BC,则
和 成立吗?为什么?
动脑筋
A
B
C
D
E
新知讲解
如图,过点A作直线MN,使MN∥DE.
∵ MN∥BC,
∴ MN∥DE∥BC.
因此AB,AC被一组平行线MN,DE,BC所截,则由平行线分线段成比例可得,
,
.
同时还可以得到
,
.
A
B
C
D
E
M
N
新知讲解
由此,得到以下结论:
平行于三角形一边的直线截其他两边, 所得的对应线段成比例.
A
B
C
D
E
例题教学
例 如图,已知AA ∥BB ∥CC ,AB=2,BC=3,A B =1.5,求B C 的长.
解 由平行线分线段成比例可知,
因此
.
A
A
B
C
C
B
即
课堂练习
1. 如图,已知l ∥l ∥l ,AG=4,GB=2,BC=10,则的值为( )
A. B. 2
C. D.
D
l
l
A
E
F
D
C
B
l
G
提示:由AG=4,GB=2,得AB=6.再根据平行线分线段成比例,即得
课堂练习
2. (邛崃市期末)如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.若AD∶AB=3∶4,AE=9,则AC等于( )
A. 6 B. 8
C. 10 D. 12
提示:运用平行线分线段对应成比例解决问题,一定要找出对应线段,并根据对应线段列出比例式.
D
A
B
C
D
E
课堂总结
这节课我们学过的基本事实或结论有哪些?请说一说.
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
两条直线被一组平行线所截, 所得的对应线段成比例(基本事实).
平行于三角形一边的直线截其他两边, 所得的对应线段成比例.
板书设计
平行线分线段成比例
平行线等分线段
平行线分线段成比例
平行于三角形一边的直线截另两边对应线段成比例.
作业布置
第71页课后练习第1、2题
1.如图, AC,BD相交于点O,直线MN过点O,且BA∥MN∥CD.已知OA=3,OB=1,OD=2,求OC的长.
A
B
O
M
N
D
C
作业布置
2.如图, 点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AB=3,AD=2,EC=1.8,求AC的长.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
