10.3实数(一)[下学期]
文档属性
| 名称 | 10.3实数(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-21 00:00:00 | ||
图片预览




文档简介
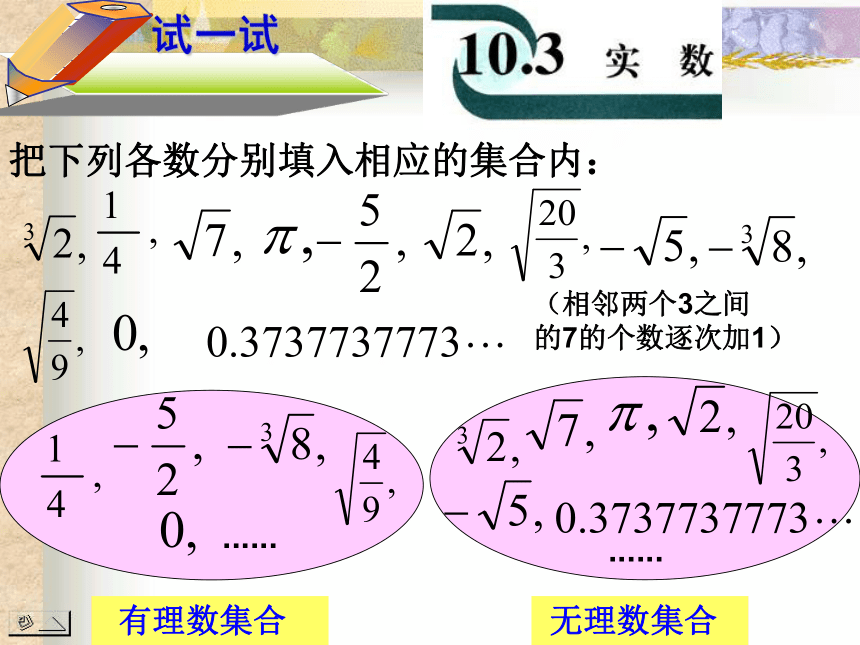
课件13张PPT。10.3 实数(一)使用计算器计算,把下列有理数写成小数的形式,你有什么发现? 事实上,任何一个有理数都可以写成有限小数或无限循环小数。 反过来,任何有限小数或无限循环小数也都是有理数 在古希腊,有一个毕达哥拉斯学派。他们信奉“一切皆数”,认为世间万物都可以用整数或整数之比来表示。你认为这个断言正确吗? 但毕达哥拉斯的学生希伯索斯却发现边长为 1 的正方形的对角线的长不能用整数或整数之比来表示。1.414213562……=3.14159265358 ……=-2.236067977 ……=-1.709975947 …… 无限不循环的小数 叫做无理数你能举出一些无理数吗?带根号的数都是无理数对吗 ?1.01001000100001 …把下列各数分别填入相应的集合内:(相邻两个3之间
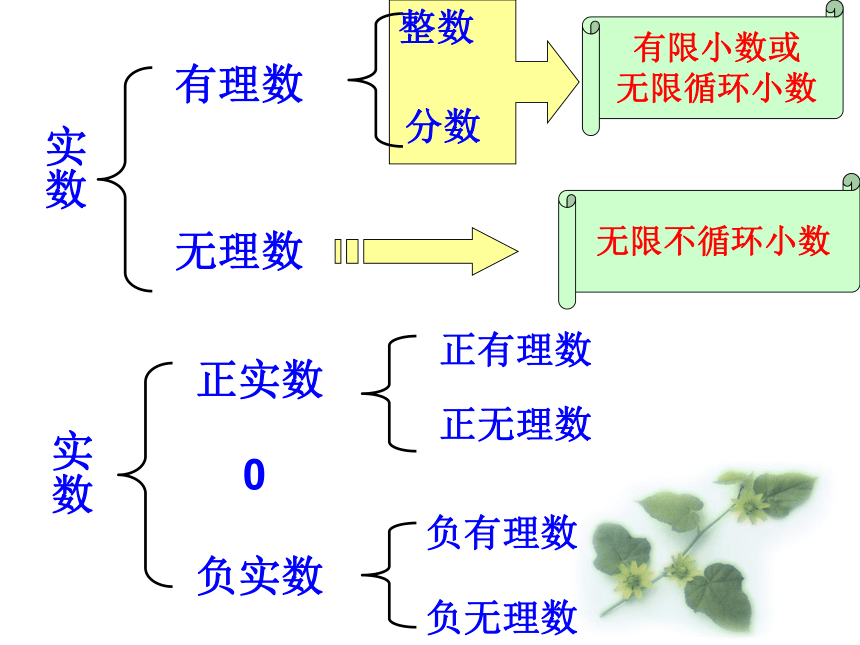
的7的个数逐次加1) 有理数集合 无理数集合............实数实数有理数无理数正实数 0负实数正有理数正无理数负有理数负无理数分数整数有限小数或
无限循环小数无限不循环小数数轴上的点与实数是一一对应的.平面直角坐标系中的点与有序实数对是一一对应的.练一练把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××这节课有什么收获?有理数的有关性质在实数范围内还适用吗?谈一谈
的7的个数逐次加1) 有理数集合 无理数集合............实数实数有理数无理数正实数 0负实数正有理数正无理数负有理数负无理数分数整数有限小数或
无限循环小数无限不循环小数数轴上的点与实数是一一对应的.平面直角坐标系中的点与有序实数对是一一对应的.练一练把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××这节课有什么收获?有理数的有关性质在实数范围内还适用吗?谈一谈
