2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册3.2.2 双曲线的简单几何性质课件(31张PPT))
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册3.2.2 双曲线的简单几何性质课件(31张PPT)) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:49:27 | ||
图片预览





文档简介
凉水塔的纵切面是双曲线,双曲线是非常优美的曲线,也是我们在生产生活中经常用到的曲线.
[问题]你能否类比椭圆的几何性质去猜想双曲线有哪些几何性质呢?
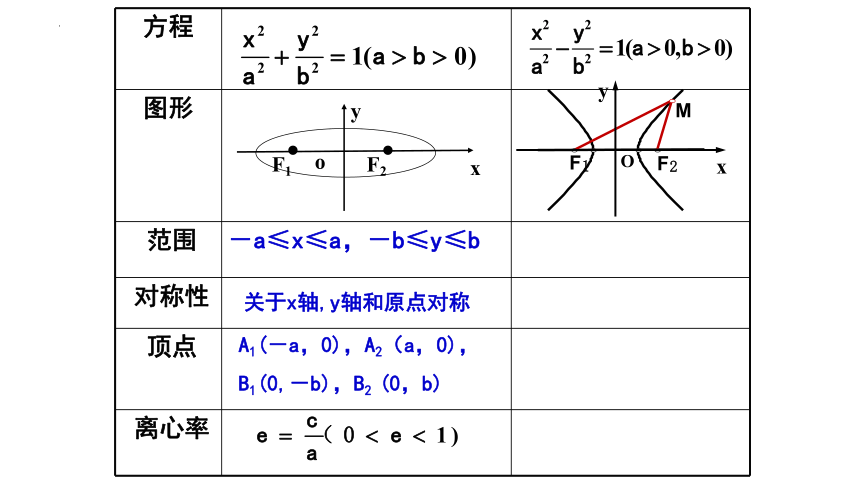
方程
图形
x
范围
对称性
顶点
离心率
关于x轴,y轴和原点对称
A1(-a,0),A2(a,0),
B1(0,-b),B2 (0,b)
-a≤x≤a,-b≤y≤b
F
2
F
1
M
x
O
y
y
o
F1
F2
·
·
3.2.2 双曲线的简单几何性质
(第一课时)
学习目标
01
02
了解双曲线简单几何性质
会结合双曲线理解其几何性质
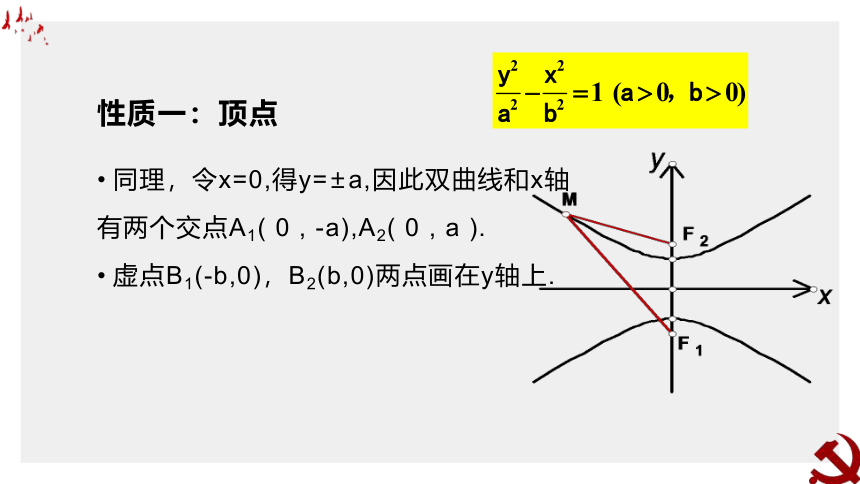
性质一:顶点
性质一:顶点
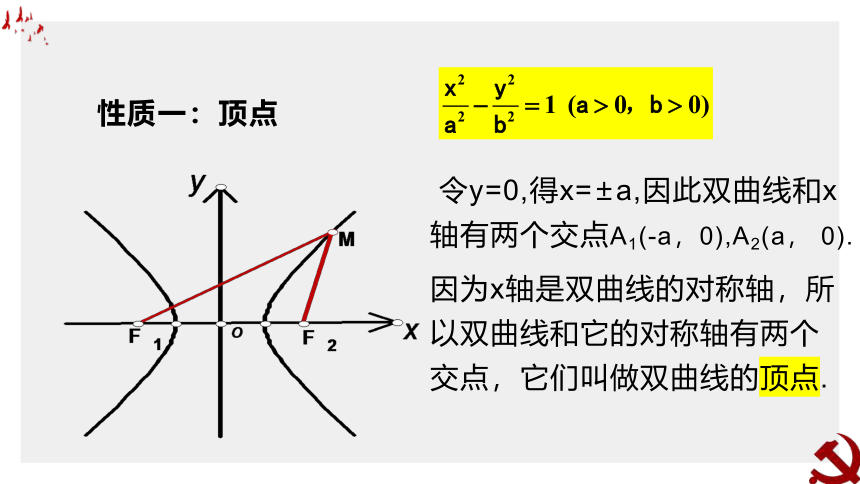
令y=0,得x=±a,因此双曲线和x轴有两个交点A1(-a,0),A2(a,?0).
因为x轴是双曲线的对称轴,所以双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点.
一:顶点
令y=0,得x=±a,因此双曲线和x轴有两个交点A1(-a,0),A2(a,?0).因为x轴是双曲线的对称轴,所以双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点.
令x=0,得y2=-b2,这个方程没有实数解,说明双曲线和y轴没有公共点,但我们也把B1(0,-b),B2(0,?b)两点画在y轴上.
一:顶点
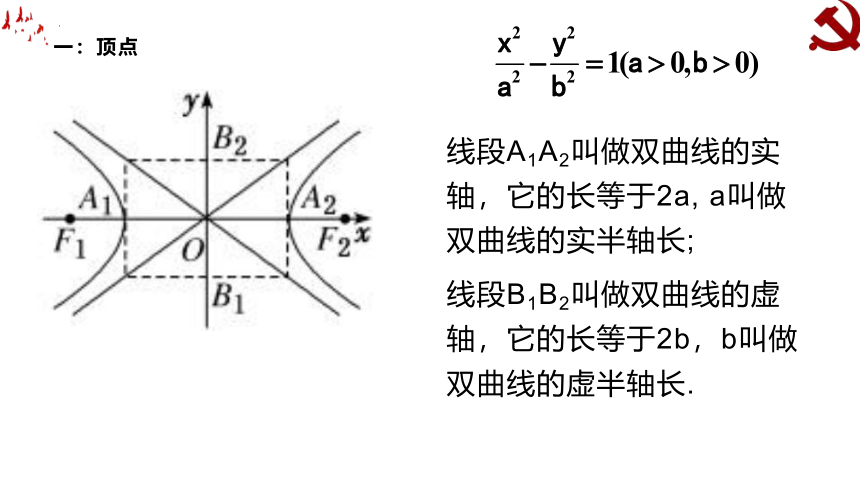
线段A1A2叫做双曲线的实轴,它的长等于2a,?a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
性质一:顶点
同理,令x=0,得y=±a,因此双曲线和x轴
有两个交点A1( 0 , -a),A2(?0 , a ).
虚点B1(-b,0),B2(b,0)两点画在y轴上.
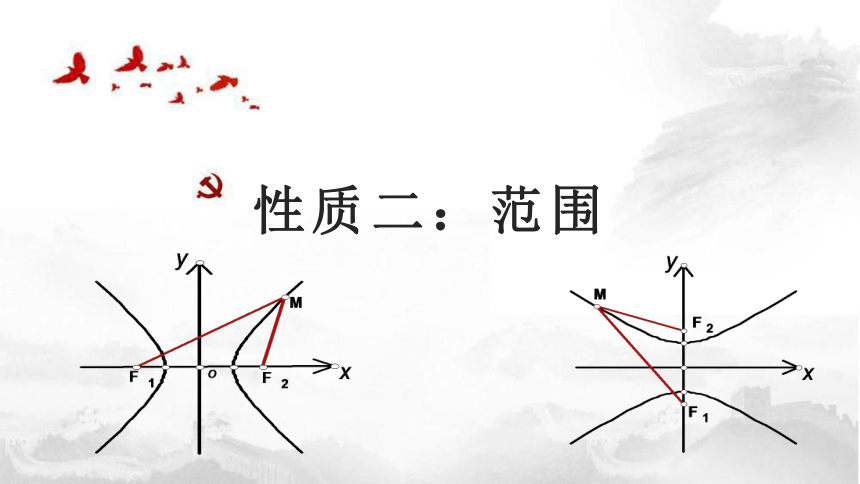
性质二:范围
二:范围
类比研究椭圆范围的方法,观察双曲线(焦点在x轴上),我们发现双曲线上点的横坐标的范围是x≤-?a,或x≥a,纵坐标的范围是y∈R.
这说明双曲线位于直线x=-a及其左侧和直线x=a及其右侧的区域。
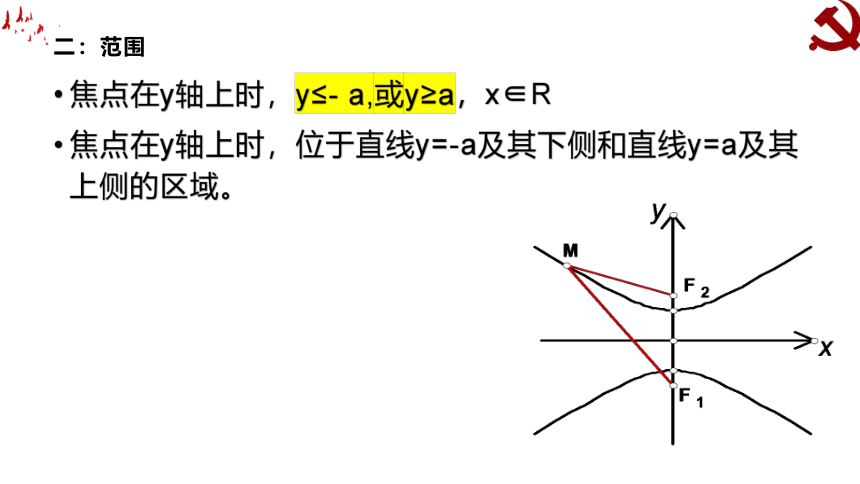
二:范围
焦点在y轴上时,y≤-?a,或y≥a,x∈R
焦点在y轴上时,位于直线y=-a及其下侧和直线y=a及其上侧的区域。
三:对称性
性质三:对称性
三:对称性
类比研究椭圆的对称性的方法,容易得到 ,双曲线
关于x轴、y轴和原点都是对称的.这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心。双曲线的对称中心叫做双曲线的中心.
四:渐近线
一般地,双曲线 ? 的两支向外延伸时,与两条直线 ± ???????? =0 逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交.
?
????????
?
性质四:渐近线
x
y
o
a
注:双曲线与它的渐近线无限接近,但永不相交
-a
b
四:渐近线
x
y
o
a
四.渐近线:
(2)当a=b时,双曲线的实轴和虚轴长度
都等于2a,称为等轴双曲线
-a
b
等轴双曲线和共轭双曲线
1.等轴双曲线:
双曲线? ,如果a=b,那么方程变为
x2-y2=a2,此时双曲线的实轴和虚轴的长都等于2a.
这时,四条直线x=±a,?y=±a围成正方形,渐近线方程为y=±x,它们互相垂直,并且平分双曲线的实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
等轴双曲线和共轭双曲线
2.共轭双曲线:
以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.
性质五:离心率
c>a>0
e>1
e是表示双曲线开口大小的一个量,e越大,开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
x
y
o
a
-a
b
例题讲解
例1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
?
解:
∴????=????2+????2=42+32=5
?
焦点坐标是(0,-5),(0,5);
?
????=????????=54
?
离心率 :
渐近线方程:
????=±43????
?
例1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
?
例2 求适合下列条件的双曲线的标准方程:
(1)焦点在????轴上,实轴长是10,虚轴长是8;
(2)焦点在????轴上,焦距是10,虚轴长是8;
?
例2 求适合下列条件的双曲线的标准方程:
(1)焦点在????轴上,实轴长是10,虚轴长是8;
?
解:设双曲线的标准方程为:
由题意可知,????=5,????=4.
双曲线的标准方程为:
?
解:设双曲线的标准方程为
由题意可知,????=5,????=4 所以????=3.
双曲线的标准方程为:
?
例2 求适合下列条件的双曲线的标准方程:
(2)焦点在????轴上,焦距是10,虚轴长是8;
?
课堂作业
求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标以及离心率:
单击此处添加副标题内容
谢谢观看
[问题]你能否类比椭圆的几何性质去猜想双曲线有哪些几何性质呢?
方程
图形
x
范围
对称性
顶点
离心率
关于x轴,y轴和原点对称
A1(-a,0),A2(a,0),
B1(0,-b),B2 (0,b)
-a≤x≤a,-b≤y≤b
F
2
F
1
M
x
O
y
y
o
F1
F2
·
·
3.2.2 双曲线的简单几何性质
(第一课时)
学习目标
01
02
了解双曲线简单几何性质
会结合双曲线理解其几何性质
性质一:顶点
性质一:顶点
令y=0,得x=±a,因此双曲线和x轴有两个交点A1(-a,0),A2(a,?0).
因为x轴是双曲线的对称轴,所以双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点.
一:顶点
令y=0,得x=±a,因此双曲线和x轴有两个交点A1(-a,0),A2(a,?0).因为x轴是双曲线的对称轴,所以双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点.
令x=0,得y2=-b2,这个方程没有实数解,说明双曲线和y轴没有公共点,但我们也把B1(0,-b),B2(0,?b)两点画在y轴上.
一:顶点
线段A1A2叫做双曲线的实轴,它的长等于2a,?a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
性质一:顶点
同理,令x=0,得y=±a,因此双曲线和x轴
有两个交点A1( 0 , -a),A2(?0 , a ).
虚点B1(-b,0),B2(b,0)两点画在y轴上.
性质二:范围
二:范围
类比研究椭圆范围的方法,观察双曲线(焦点在x轴上),我们发现双曲线上点的横坐标的范围是x≤-?a,或x≥a,纵坐标的范围是y∈R.
这说明双曲线位于直线x=-a及其左侧和直线x=a及其右侧的区域。
二:范围
焦点在y轴上时,y≤-?a,或y≥a,x∈R
焦点在y轴上时,位于直线y=-a及其下侧和直线y=a及其上侧的区域。
三:对称性
性质三:对称性
三:对称性
类比研究椭圆的对称性的方法,容易得到 ,双曲线
关于x轴、y轴和原点都是对称的.这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心。双曲线的对称中心叫做双曲线的中心.
四:渐近线
一般地,双曲线 ? 的两支向外延伸时,与两条直线 ± ???????? =0 逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交.
?
????????
?
性质四:渐近线
x
y
o
a
注:双曲线与它的渐近线无限接近,但永不相交
-a
b
四:渐近线
x
y
o
a
四.渐近线:
(2)当a=b时,双曲线的实轴和虚轴长度
都等于2a,称为等轴双曲线
-a
b
等轴双曲线和共轭双曲线
1.等轴双曲线:
双曲线? ,如果a=b,那么方程变为
x2-y2=a2,此时双曲线的实轴和虚轴的长都等于2a.
这时,四条直线x=±a,?y=±a围成正方形,渐近线方程为y=±x,它们互相垂直,并且平分双曲线的实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
等轴双曲线和共轭双曲线
2.共轭双曲线:
以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.
性质五:离心率
c>a>0
e>1
e是表示双曲线开口大小的一个量,e越大,开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
x
y
o
a
-a
b
例题讲解
例1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
?
解:
∴????=????2+????2=42+32=5
?
焦点坐标是(0,-5),(0,5);
?
????=????????=54
?
离心率 :
渐近线方程:
????=±43????
?
例1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
?
例2 求适合下列条件的双曲线的标准方程:
(1)焦点在????轴上,实轴长是10,虚轴长是8;
(2)焦点在????轴上,焦距是10,虚轴长是8;
?
例2 求适合下列条件的双曲线的标准方程:
(1)焦点在????轴上,实轴长是10,虚轴长是8;
?
解:设双曲线的标准方程为:
由题意可知,????=5,????=4.
双曲线的标准方程为:
?
解:设双曲线的标准方程为
由题意可知,????=5,????=4 所以????=3.
双曲线的标准方程为:
?
例2 求适合下列条件的双曲线的标准方程:
(2)焦点在????轴上,焦距是10,虚轴长是8;
?
课堂作业
求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标以及离心率:
单击此处添加副标题内容
谢谢观看
