立方根
图片预览









文档简介
课件30张PPT。10.2 立 方 根本课的教学重点:立方根的概念及性质;
本课的教学难点:求一个数的立方根。1. 想一想:
平方根是如何定义的?平方根有哪些性质?一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根;
正数有___个平方根,它们_______;
0的平方根是__________;
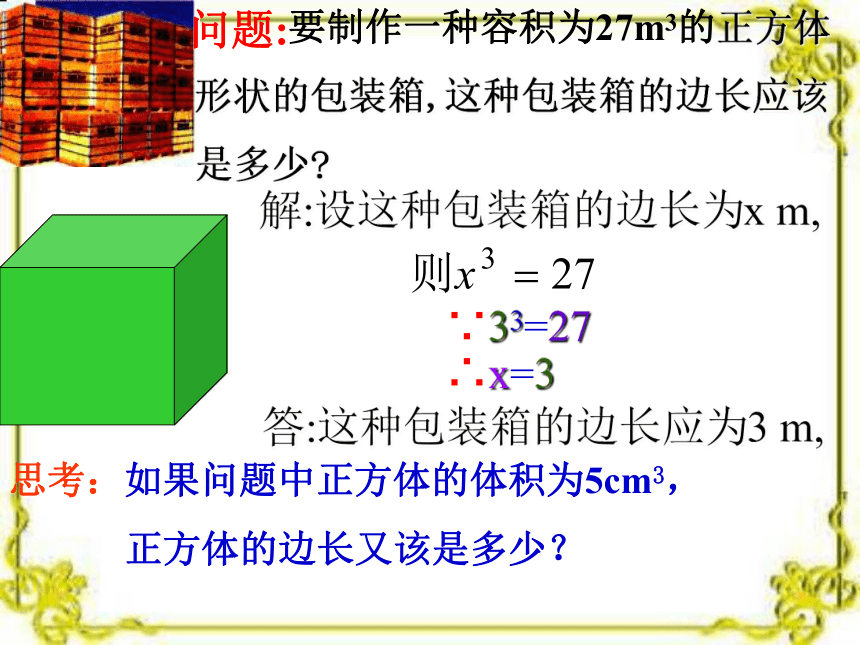
负数__________________. 活动(1) 创设情境,复旧导新 .16的平方根是______-16的平方根是________0的平方根是________没有平方根0 一个正数有正负两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.你还记得吗2.计算:解: 要制作一种容积为27m3的正方体
形状的包装箱,这种包装箱的边长应该
是多少?解:设这种包装箱的边长为x m,∵33=27∴x=3问题:答:这种包装箱的边长应为3 m,思考:如果问题中正方体的体积为5cm3,
正方体的边长又该是多少?
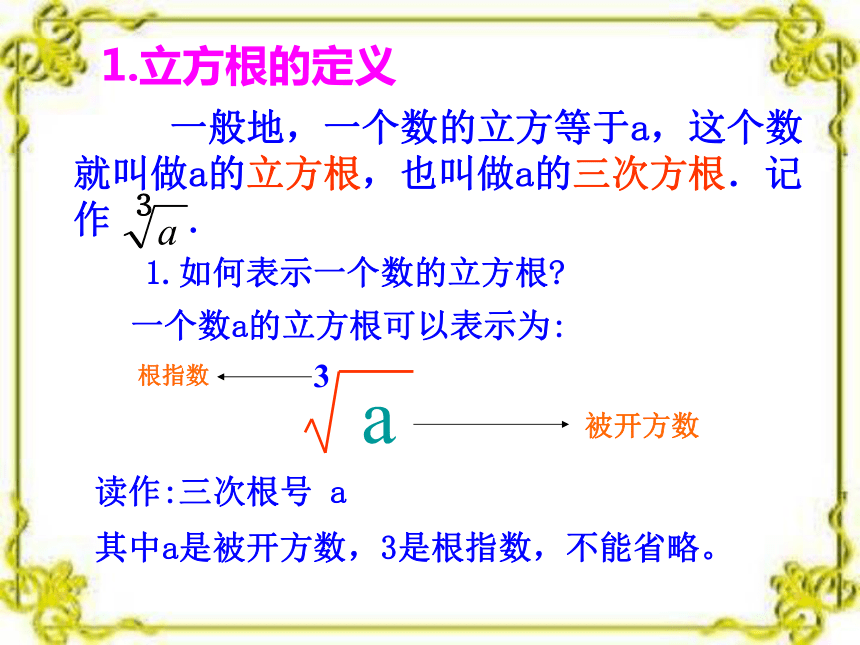
1.立方根的概念.
一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根). 用式子表示,如果X3 =a,那么X叫做a的立方根.a的平方根怎样表示?答:或类似的请同学们想一想a的立方根怎样表示?立方根的表示方法:1.立方根的定义1.如何表示一个数的立方根?一个数a的立方根可以表示为:根指数被开方数其中a是被开方数,3是根指数,不能省略。读作:三次根号 a如:33=27 则把3叫做27的立方根,即 X叫a的四次方根思考:如果正方体的体积为5cm3,正方体的边长又该是多少?设正方体的边长为X,则 2.求一个数的立方根的运算,叫做开立方立方开立方互逆到现在我们学了几种运算?+,-,x,÷,乘方,开方(开平方,开立方)逆2.立方根的性质探究1. 根据立方根的意义填空. 因为 =8,所以8的立方根是( ) 因为( ) =0.125,所以0.125的立方是( )因为( ) =0,所以0的立方根是( )因为 ( ) =-8,所以-8的立方根是( )因为( ) =- ,所以- 的立方( ) 02-20-2你能看出正数,0,负数的立方根各有什么特点?正数有立方根吗?如果有,有几个?想一想负数呢?零呢?一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。(1)立方根的特征讨论:你能归纳出平方根和立方根的异同点吗?有两个互为相反数有一个,是正数无平方根零有一个,是负数零正数负数零练一练1.判断下列说法是否正确,并说明理由x(2) 25的平方根是5x(3) -64没有立方根x(4) -4的平方根是x(5) 0的平方根和立方根都是0√立方根是它本身的数有那些?有1, -1, 0平方根是它本身的数呢?只有0想一想引伸探究2猜一猜:你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?=-2-2=-3-3例:求下列各式的值解:归纳: 求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.用计算器求125的立方根用计算器求1845的立方根
(1)1的平方根是____;立方根为____;算术平方根为__.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:探究3先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?归纳: 被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.练习:请同学们完成教材第171页的第1题,第4题.议一议,,,你会区别下列的数吗?表示a的算术平方根表示a的平方根或a的二次方根表示a的立方根或a的三次方根表示a的四次方根课堂练习2:2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=8 一个自然数的算术平方根是a,那么与这个自然数相邻的下一个自然数的平方根是_________;立方根是________. 探究题 已知半径为r 的球,其体积 的计 算公式为 . 如果甲、乙两球 体积的比为1 :8,则甲、乙两球的半径比为 .Rr乙甲 5.跳一跳:课堂小结相同点:
①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同1.立方根的定义,性质,计算.2.立方根与平方根的异同小结:1、平方根的定义:如果一个数的平方等于a,那么这个数叫做a的平方根。a的平方根用±2、平方根的性质
(1)一个正数有两个平方根,这两个平方根互为相反数
(2)0的平方根还是0
(3)负数没有平方根3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2 即1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根。a的立方根用 表示2、立方根的性质
(1)正数的立方根还是正数
(2)0的平方根还是0
(3)负数的立方根还是负数3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2 即再见2、选做题:计算下列各式的值:
①
活动(5) 布置作业,巩固新知 .
(1)1的平方根是____;立方根为____;算术平方根为__.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:试一试
1.已知:x-2 的平方根是±2,2x+y+7 的
立方根是3,求 的平方根和立方根.
2.已知 ,
求 的值.
作业: P138 A组 2. 3.
思考:一个正方体的体积变为原来的n倍,它的棱长变为原来的多少倍?
本课的教学难点:求一个数的立方根。1. 想一想:
平方根是如何定义的?平方根有哪些性质?一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根;
正数有___个平方根,它们_______;
0的平方根是__________;
负数__________________. 活动(1) 创设情境,复旧导新 .16的平方根是______-16的平方根是________0的平方根是________没有平方根0 一个正数有正负两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.你还记得吗2.计算:解: 要制作一种容积为27m3的正方体
形状的包装箱,这种包装箱的边长应该
是多少?解:设这种包装箱的边长为x m,∵33=27∴x=3问题:答:这种包装箱的边长应为3 m,思考:如果问题中正方体的体积为5cm3,
正方体的边长又该是多少?
1.立方根的概念.
一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根). 用式子表示,如果X3 =a,那么X叫做a的立方根.a的平方根怎样表示?答:或类似的请同学们想一想a的立方根怎样表示?立方根的表示方法:1.立方根的定义1.如何表示一个数的立方根?一个数a的立方根可以表示为:根指数被开方数其中a是被开方数,3是根指数,不能省略。读作:三次根号 a如:33=27 则把3叫做27的立方根,即 X叫a的四次方根思考:如果正方体的体积为5cm3,正方体的边长又该是多少?设正方体的边长为X,则 2.求一个数的立方根的运算,叫做开立方立方开立方互逆到现在我们学了几种运算?+,-,x,÷,乘方,开方(开平方,开立方)逆2.立方根的性质探究1. 根据立方根的意义填空. 因为 =8,所以8的立方根是( ) 因为( ) =0.125,所以0.125的立方是( )因为( ) =0,所以0的立方根是( )因为 ( ) =-8,所以-8的立方根是( )因为( ) =- ,所以- 的立方( ) 02-20-2你能看出正数,0,负数的立方根各有什么特点?正数有立方根吗?如果有,有几个?想一想负数呢?零呢?一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。(1)立方根的特征讨论:你能归纳出平方根和立方根的异同点吗?有两个互为相反数有一个,是正数无平方根零有一个,是负数零正数负数零练一练1.判断下列说法是否正确,并说明理由x(2) 25的平方根是5x(3) -64没有立方根x(4) -4的平方根是x(5) 0的平方根和立方根都是0√立方根是它本身的数有那些?有1, -1, 0平方根是它本身的数呢?只有0想一想引伸探究2猜一猜:你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?=-2-2=-3-3例:求下列各式的值解:归纳: 求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.用计算器求125的立方根用计算器求1845的立方根
(1)1的平方根是____;立方根为____;算术平方根为__.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:探究3先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?归纳: 被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.练习:请同学们完成教材第171页的第1题,第4题.议一议,,,你会区别下列的数吗?表示a的算术平方根表示a的平方根或a的二次方根表示a的立方根或a的三次方根表示a的四次方根课堂练习2:2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=8 一个自然数的算术平方根是a,那么与这个自然数相邻的下一个自然数的平方根是_________;立方根是________. 探究题 已知半径为r 的球,其体积 的计 算公式为 . 如果甲、乙两球 体积的比为1 :8,则甲、乙两球的半径比为 .Rr乙甲 5.跳一跳:课堂小结相同点:
①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同1.立方根的定义,性质,计算.2.立方根与平方根的异同小结:1、平方根的定义:如果一个数的平方等于a,那么这个数叫做a的平方根。a的平方根用±2、平方根的性质
(1)一个正数有两个平方根,这两个平方根互为相反数
(2)0的平方根还是0
(3)负数没有平方根3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2 即1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根。a的立方根用 表示2、立方根的性质
(1)正数的立方根还是正数
(2)0的平方根还是0
(3)负数的立方根还是负数3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2 即再见2、选做题:计算下列各式的值:
①
活动(5) 布置作业,巩固新知 .
(1)1的平方根是____;立方根为____;算术平方根为__.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:试一试
1.已知:x-2 的平方根是±2,2x+y+7 的
立方根是3,求 的平方根和立方根.
2.已知 ,
求 的值.
作业: P138 A组 2. 3.
思考:一个正方体的体积变为原来的n倍,它的棱长变为原来的多少倍?
