人教版八年级数学上册15.2分式的运算练习卷(含解析)
文档属性
| 名称 | 人教版八年级数学上册15.2分式的运算练习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 223.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 20:10:09 | ||
图片预览




文档简介
15.2 分式的运算(练习卷)-人教版八年级上册
一.选择题
1.如图,若x为正整数,则表示的值的点落在( )
A.① B.② C.③ D.④
2.已知=3,=4,=5,则=( )
A. B. C. D.
3.某人从A地到B地的速度为v1,从B地返回A地的速度为v2,若v1≠v2,则此人从A地到B地往返一次的平均速度是( )
A. B.
C.以上都不对
4.化简(1+)÷的结果是( )
A.1 B. C. D.﹣
.阅读材料:在处理分数和分式的问题时,有时由于分子大于分母,或分子的次数高于分母的次数,在实际运算时难度较大,这时,我们可将分数(分式)拆分成一个整数(整式)与一个真分数(真分式)的和(差)的形式,通过对它的简单分析来解决问题,我们称这种方法为分离常数法,此法在处理分式或整除问题时颇为有效.将分式分离常数可类比假分数变形带分数的方法进行.
如:==a+=a﹣1+,这样,分式就拆分成一个分式与一个整式a﹣1的和的形式,下列说法正确的有( )个.
①若x为整数,为负整数,则x=﹣3;
②6<≤9;
③若分式拆分成一个整式与一个真分式(分子为整数)的和(差)的形式为:5m﹣11+(整式部分对应等于5m﹣11,真分式部分对应等于),则m2+n2+mn的最小值为27.
A.0 B.1 C.2 D.3
.下列计算错误的是( )
A. B.
C. D.
.如果a+b=3,那么的值是( )
A.3 B.﹣3 C. D.﹣
.老师出了一道题:计算+,对于下面这三名同学的做法,你的判断是( )
乐乐的做法是:原式=﹣==;
淇淇的做法是:原式=(x+3)(x﹣2)+(2﹣x)=x2+x﹣6+2﹣x=x2﹣4;
嘉嘉的做法是:原式=﹣=﹣==1.
A.嘉嘉的做法是正确的
B.淇淇的做法是正确的
C.乐乐的做法是正确的
D.三名同学的做法均不正确
.若代数式(8﹣2x)0﹣有意义,则x的取值范围是( )
A.x>4 B.x≥4 C.x≠2且x≠4 D.x≠2且x≥4
.规定一种新的运算“JQx→+∞”,其中A和B是关于x的多项式.当A的次数小于B的次数时,JQx→+∞=0;当A的次数等于B的次数时,JQx→+∞的值为A、B的最高次项的系数的商.当A的次数大于B的次数时,JQx→+∞不存在.
例:JQx→+∞=0,JQx→+∞.
若,则JQx→+∞的值为( )
A.0 B. C. D.不存在
二.填空题
.纳米是一种长度单位:1纳米=10﹣9米,已知某植物花粉的直径为3500纳米,那么用科学记数法表示该种花粉的直径为 米.
.已知=,则的值为 .
.化简÷(1+)的结果是 .
.若x+y+z=0,则x(+)+y(+)+z(+)的值是 .
.阅读理解:我们知道:当a是c的因数时,(a、c为整数)的值是整数.例如,当a=±1或±2时,的值是整数;又如,因为=3,所以当m=±1或±5时,的值是整数.
(1)如果分式的值是整数,那么a的正整数值是 .
(2)如果分式的值是整数,那么x的负整数值是 .
三.解答题
.(1)解不等式:﹣x<3﹣;
(2)计算:÷(a+1﹣).
.(1)求不等式组的整数解.
(2)先化简,再求值:,其中m是16的算术平方根.
.我们小学学分数时学过真分数和假分数,初中我们又学习了分式,现在我们来了解一下什么是“真分式”和“假分式”,对于只含有一个字母的分式,当分子的次数小于分母的次数时,称为“真分式”,如;当分子的次数大于或等于分母的次数时,称为“假分式”,如:,.假分式也可以化为带分式的形式,即为整式与“真分式”的和的形式,如:,.
(1)分式是分式 (填“真”或“假”).
(2)请将分式化为带分式的形式,问当的值为整数时,求整数x的所有可能值.
.先化简,再求值:,其中x=﹣4.
下面是小宇同学的化简过程,请认真阅读并完成相应任务.
解:原式=…第一步
=…第二步
…第三步
=.…第四步
任务一:
填空:①以上化简步骤中,第 步是约分得到的,约分的依据是 ;
②第 步开始出现错误,这一步错误的原因是 .
任务二:请直接写出该分式化简后的正确结果,并代入求值.
.请认真观察图形,解答下列问题:
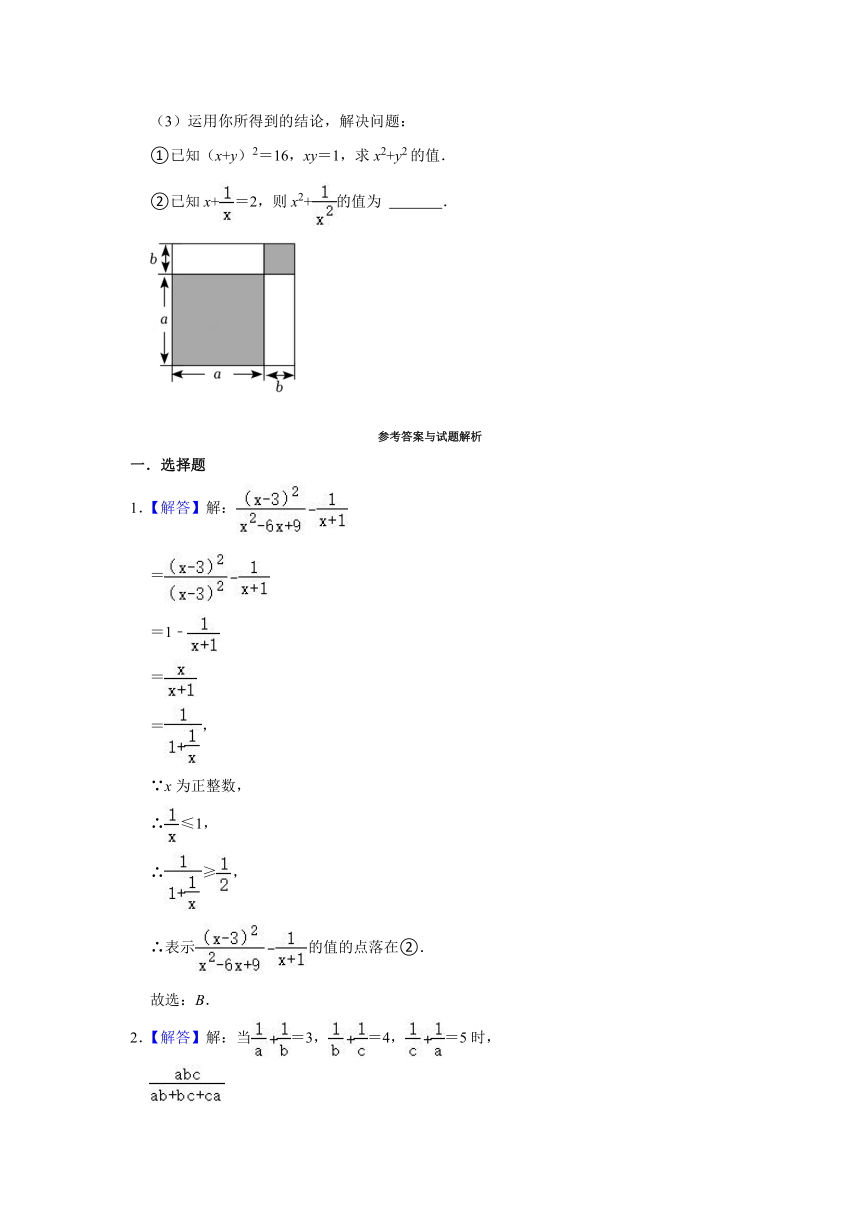
(1)根据图中条件,试用两种不同方法表示阴影部分的面积.方法1: ;方法2: ;
(2)从中你能发现什么结论?请用等式表示该结论: .
(3)运用你所得到的结论,解决问题:
①已知(x+y)2=16,xy=1,求x2+y2的值.
②已知x+=2,则x2+的值为 .
参考答案与试题解析
一.选择题
1.【解答】解:
=
=1﹣
=
=,
∵x为正整数,
∴≤1,
∴≥,
∴表示的值的点落在②.
故选:B.
2.【解答】解:当=3,=4,=5时,
=
=
=
=
=
=
=.
故选:D.
3.【解答】解:本题没有AB两地的单程,可设为1,那么总路程为2,
总时间为 +.平均速度=2÷( +)=.
故选:C.
4.【解答】解:(1+)÷
=(+)÷
=
=
=1,
故选:A.
.【解答】解:∵为负整数,
∴<0,
∴或,
解第一个不等式组得:﹣4<x<﹣2,
解第二个不等式组得:无解,
∴﹣4<x<﹣2,
∵x为整数,
∴x=﹣3,
故①的结论正确;
∵=6+,
又x2≥0,
∴>0,且x2+2有最小值2,
∴由最大值3,
∴6<6+≤9,
∴②的结论正确;
∵==5(x+2)﹣11﹣,
∴m=x+2,n﹣6=﹣(x+2),
∴m=x+2,n=4﹣x.
∴m2+n2+mn
=(m+n)2﹣mn
=36﹣(﹣x2+2x+8)
=x2﹣2x+28
=(x﹣1)2+27,
∵(x﹣1)2≥0,
∴m2+n2+mn有最小值为27,
∴③的结论正确,
故选:D.
.【解答】解:∵=,
∴A选项计算正确;
∵,
∴B选项计算正确;
∵=,
∴C选项计算错误;
∵=,
∴D选项计算正确.
综上,计算错误的是C.
故选:C.
.【解答】解:
=
=
=a+b,
当a+b=3时,原式=3,
故选:A.
.【解答】解:原式=,
=,
=,
=1.
∴嘉嘉的做法正确,
故选:A.
.【解答】解:由题意得:
.
∴x≠2且x≠4.
故选:C.
.【解答】解:
=÷
=
=,
∴A的次数等于B的次数,
∴JQx→+∞=,
故选:C.
二.填空题
.【解答】解:3500纳米=3.5×103×10﹣9米=3.5×10﹣6米,
故答案为:3.5×10﹣6.
.【解答】解:∵=,
∴﹣3(a﹣b)=ab.
原式==﹣3.
故答案为:﹣3.
.【解答】解:原式=÷
=
=.
故答案为:.
.【解答】解:原式=+++++
=++
∵x+y+z=0,
∴x=﹣(y+z),y=﹣(x+z),z=﹣(x+y),
∴原式=++
=﹣1﹣1﹣1
=﹣3.
故答案为:﹣3.
.【解答】解:(1)
=
=1+,
∵分式的值是整数,
∴,,
解得:a=﹣4或a=﹣2或a=﹣7(不符合题意舍去),a=2,
故答案为:2;
(2)
=
=
=
=1﹣,
∵分式的值是整数,
∴=±1或=±3,
解得:x=1或x=7或x=13(不符合题意舍去),x=﹣5.
故答案为:﹣5.
三.解答题
.【解答】解:(1)﹣x<3﹣,
去分母,得:4(1﹣x)﹣12x<36﹣3(x+2),
去括号,得:4﹣4x﹣12x<36﹣3x﹣6,
移项及合并同类项,得:﹣13x<26,
系数化为1,得:x>﹣2;
(2)÷(a+1﹣)
=÷
=
=
=.
.【解答】解:(1),
解不等式①,得:x>﹣1,
解不等式②,得:x≤2,
∴该不等式组的解集为﹣1<x≤2,
∴该不等式组的整数解是0,1,2;
(2)
=÷
=
=
=,
∵m是16的算术平方根,
∴m=4,
当m=4时,原式==.
.【解答】解:(1)∵分子次数高于分母次数,
∴改分式是“假分式”.
故答案为:假.
(2)原式==2x+1﹣.
∵原分式的值是整数,
∴2x﹣1是2因数,
∴2x﹣1=±1,±2,
∵x是整数,
∴x=1,0.
.【解答】解:任务一:
①以上化简步骤中,第三步是约分得到的,约分的依据是分式的基本性质;
故答案为:三,分式的基本性质;
②第一步开始出现错误,这一步错误的原因是添括号时,括号里面的第二项没有变号;
故答案为:一,添括号时,括号里面的第二项没有变号;
任务二:
=
=
=
=﹣(x+2)
=﹣x﹣2,
当x=﹣4时,原式=﹣(﹣4)﹣2=4﹣2=2.
.【解答】解:(1)由图可得:
图中阴影部分的面积为:a2+b2或(a+b)2﹣2ab,
故答案为:a2+b2;(a+b)2﹣2ab;
(2)结论:a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)①∵(x+y)2=16,xy=1,
∴x2+y2
=(x+y)2﹣2xy
=16﹣2×1
=16﹣2
=14;
②∵x+=2,
∴(x+)2=4,x =1,
∴x2+
=(x+)2﹣2x
=4﹣2×1
=4﹣2
=2,
故答案为:2.
一.选择题
1.如图,若x为正整数,则表示的值的点落在( )
A.① B.② C.③ D.④
2.已知=3,=4,=5,则=( )
A. B. C. D.
3.某人从A地到B地的速度为v1,从B地返回A地的速度为v2,若v1≠v2,则此人从A地到B地往返一次的平均速度是( )
A. B.
C.以上都不对
4.化简(1+)÷的结果是( )
A.1 B. C. D.﹣
.阅读材料:在处理分数和分式的问题时,有时由于分子大于分母,或分子的次数高于分母的次数,在实际运算时难度较大,这时,我们可将分数(分式)拆分成一个整数(整式)与一个真分数(真分式)的和(差)的形式,通过对它的简单分析来解决问题,我们称这种方法为分离常数法,此法在处理分式或整除问题时颇为有效.将分式分离常数可类比假分数变形带分数的方法进行.
如:==a+=a﹣1+,这样,分式就拆分成一个分式与一个整式a﹣1的和的形式,下列说法正确的有( )个.
①若x为整数,为负整数,则x=﹣3;
②6<≤9;
③若分式拆分成一个整式与一个真分式(分子为整数)的和(差)的形式为:5m﹣11+(整式部分对应等于5m﹣11,真分式部分对应等于),则m2+n2+mn的最小值为27.
A.0 B.1 C.2 D.3
.下列计算错误的是( )
A. B.
C. D.
.如果a+b=3,那么的值是( )
A.3 B.﹣3 C. D.﹣
.老师出了一道题:计算+,对于下面这三名同学的做法,你的判断是( )
乐乐的做法是:原式=﹣==;
淇淇的做法是:原式=(x+3)(x﹣2)+(2﹣x)=x2+x﹣6+2﹣x=x2﹣4;
嘉嘉的做法是:原式=﹣=﹣==1.
A.嘉嘉的做法是正确的
B.淇淇的做法是正确的
C.乐乐的做法是正确的
D.三名同学的做法均不正确
.若代数式(8﹣2x)0﹣有意义,则x的取值范围是( )
A.x>4 B.x≥4 C.x≠2且x≠4 D.x≠2且x≥4
.规定一种新的运算“JQx→+∞”,其中A和B是关于x的多项式.当A的次数小于B的次数时,JQx→+∞=0;当A的次数等于B的次数时,JQx→+∞的值为A、B的最高次项的系数的商.当A的次数大于B的次数时,JQx→+∞不存在.
例:JQx→+∞=0,JQx→+∞.
若,则JQx→+∞的值为( )
A.0 B. C. D.不存在
二.填空题
.纳米是一种长度单位:1纳米=10﹣9米,已知某植物花粉的直径为3500纳米,那么用科学记数法表示该种花粉的直径为 米.
.已知=,则的值为 .
.化简÷(1+)的结果是 .
.若x+y+z=0,则x(+)+y(+)+z(+)的值是 .
.阅读理解:我们知道:当a是c的因数时,(a、c为整数)的值是整数.例如,当a=±1或±2时,的值是整数;又如,因为=3,所以当m=±1或±5时,的值是整数.
(1)如果分式的值是整数,那么a的正整数值是 .
(2)如果分式的值是整数,那么x的负整数值是 .
三.解答题
.(1)解不等式:﹣x<3﹣;
(2)计算:÷(a+1﹣).
.(1)求不等式组的整数解.
(2)先化简,再求值:,其中m是16的算术平方根.
.我们小学学分数时学过真分数和假分数,初中我们又学习了分式,现在我们来了解一下什么是“真分式”和“假分式”,对于只含有一个字母的分式,当分子的次数小于分母的次数时,称为“真分式”,如;当分子的次数大于或等于分母的次数时,称为“假分式”,如:,.假分式也可以化为带分式的形式,即为整式与“真分式”的和的形式,如:,.
(1)分式是分式 (填“真”或“假”).
(2)请将分式化为带分式的形式,问当的值为整数时,求整数x的所有可能值.
.先化简,再求值:,其中x=﹣4.
下面是小宇同学的化简过程,请认真阅读并完成相应任务.
解:原式=…第一步
=…第二步
…第三步
=.…第四步
任务一:
填空:①以上化简步骤中,第 步是约分得到的,约分的依据是 ;
②第 步开始出现错误,这一步错误的原因是 .
任务二:请直接写出该分式化简后的正确结果,并代入求值.
.请认真观察图形,解答下列问题:
(1)根据图中条件,试用两种不同方法表示阴影部分的面积.方法1: ;方法2: ;
(2)从中你能发现什么结论?请用等式表示该结论: .
(3)运用你所得到的结论,解决问题:
①已知(x+y)2=16,xy=1,求x2+y2的值.
②已知x+=2,则x2+的值为 .
参考答案与试题解析
一.选择题
1.【解答】解:
=
=1﹣
=
=,
∵x为正整数,
∴≤1,
∴≥,
∴表示的值的点落在②.
故选:B.
2.【解答】解:当=3,=4,=5时,
=
=
=
=
=
=
=.
故选:D.
3.【解答】解:本题没有AB两地的单程,可设为1,那么总路程为2,
总时间为 +.平均速度=2÷( +)=.
故选:C.
4.【解答】解:(1+)÷
=(+)÷
=
=
=1,
故选:A.
.【解答】解:∵为负整数,
∴<0,
∴或,
解第一个不等式组得:﹣4<x<﹣2,
解第二个不等式组得:无解,
∴﹣4<x<﹣2,
∵x为整数,
∴x=﹣3,
故①的结论正确;
∵=6+,
又x2≥0,
∴>0,且x2+2有最小值2,
∴由最大值3,
∴6<6+≤9,
∴②的结论正确;
∵==5(x+2)﹣11﹣,
∴m=x+2,n﹣6=﹣(x+2),
∴m=x+2,n=4﹣x.
∴m2+n2+mn
=(m+n)2﹣mn
=36﹣(﹣x2+2x+8)
=x2﹣2x+28
=(x﹣1)2+27,
∵(x﹣1)2≥0,
∴m2+n2+mn有最小值为27,
∴③的结论正确,
故选:D.
.【解答】解:∵=,
∴A选项计算正确;
∵,
∴B选项计算正确;
∵=,
∴C选项计算错误;
∵=,
∴D选项计算正确.
综上,计算错误的是C.
故选:C.
.【解答】解:
=
=
=a+b,
当a+b=3时,原式=3,
故选:A.
.【解答】解:原式=,
=,
=,
=1.
∴嘉嘉的做法正确,
故选:A.
.【解答】解:由题意得:
.
∴x≠2且x≠4.
故选:C.
.【解答】解:
=÷
=
=,
∴A的次数等于B的次数,
∴JQx→+∞=,
故选:C.
二.填空题
.【解答】解:3500纳米=3.5×103×10﹣9米=3.5×10﹣6米,
故答案为:3.5×10﹣6.
.【解答】解:∵=,
∴﹣3(a﹣b)=ab.
原式==﹣3.
故答案为:﹣3.
.【解答】解:原式=÷
=
=.
故答案为:.
.【解答】解:原式=+++++
=++
∵x+y+z=0,
∴x=﹣(y+z),y=﹣(x+z),z=﹣(x+y),
∴原式=++
=﹣1﹣1﹣1
=﹣3.
故答案为:﹣3.
.【解答】解:(1)
=
=1+,
∵分式的值是整数,
∴,,
解得:a=﹣4或a=﹣2或a=﹣7(不符合题意舍去),a=2,
故答案为:2;
(2)
=
=
=
=1﹣,
∵分式的值是整数,
∴=±1或=±3,
解得:x=1或x=7或x=13(不符合题意舍去),x=﹣5.
故答案为:﹣5.
三.解答题
.【解答】解:(1)﹣x<3﹣,
去分母,得:4(1﹣x)﹣12x<36﹣3(x+2),
去括号,得:4﹣4x﹣12x<36﹣3x﹣6,
移项及合并同类项,得:﹣13x<26,
系数化为1,得:x>﹣2;
(2)÷(a+1﹣)
=÷
=
=
=.
.【解答】解:(1),
解不等式①,得:x>﹣1,
解不等式②,得:x≤2,
∴该不等式组的解集为﹣1<x≤2,
∴该不等式组的整数解是0,1,2;
(2)
=÷
=
=
=,
∵m是16的算术平方根,
∴m=4,
当m=4时,原式==.
.【解答】解:(1)∵分子次数高于分母次数,
∴改分式是“假分式”.
故答案为:假.
(2)原式==2x+1﹣.
∵原分式的值是整数,
∴2x﹣1是2因数,
∴2x﹣1=±1,±2,
∵x是整数,
∴x=1,0.
.【解答】解:任务一:
①以上化简步骤中,第三步是约分得到的,约分的依据是分式的基本性质;
故答案为:三,分式的基本性质;
②第一步开始出现错误,这一步错误的原因是添括号时,括号里面的第二项没有变号;
故答案为:一,添括号时,括号里面的第二项没有变号;
任务二:
=
=
=
=﹣(x+2)
=﹣x﹣2,
当x=﹣4时,原式=﹣(﹣4)﹣2=4﹣2=2.
.【解答】解:(1)由图可得:
图中阴影部分的面积为:a2+b2或(a+b)2﹣2ab,
故答案为:a2+b2;(a+b)2﹣2ab;
(2)结论:a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)①∵(x+y)2=16,xy=1,
∴x2+y2
=(x+y)2﹣2xy
=16﹣2×1
=16﹣2
=14;
②∵x+=2,
∴(x+)2=4,x =1,
∴x2+
=(x+)2﹣2x
=4﹣2×1
=4﹣2
=2,
故答案为:2.
