4.4对数函数及其性质 教案-2022-2023学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.4对数函数及其性质 教案-2022-2023学年高一上学期数学人教A版(2019)必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 202.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览


文档简介
姓名 学生姓名 填写时间
学科 数 学 年级 高一 教材版本 人教版
阶段 第( )周 观察期:□ 维护期:□
课题名称 对数函数 课时计划 第( )次课 共 ( )课时 上课时间
教学目标 掌握对数函数的基本性质 能够理解对数函数的应用
教学重点 对数函数图像特征和性质
教学难点 对数函数与其他函数复合时的性质
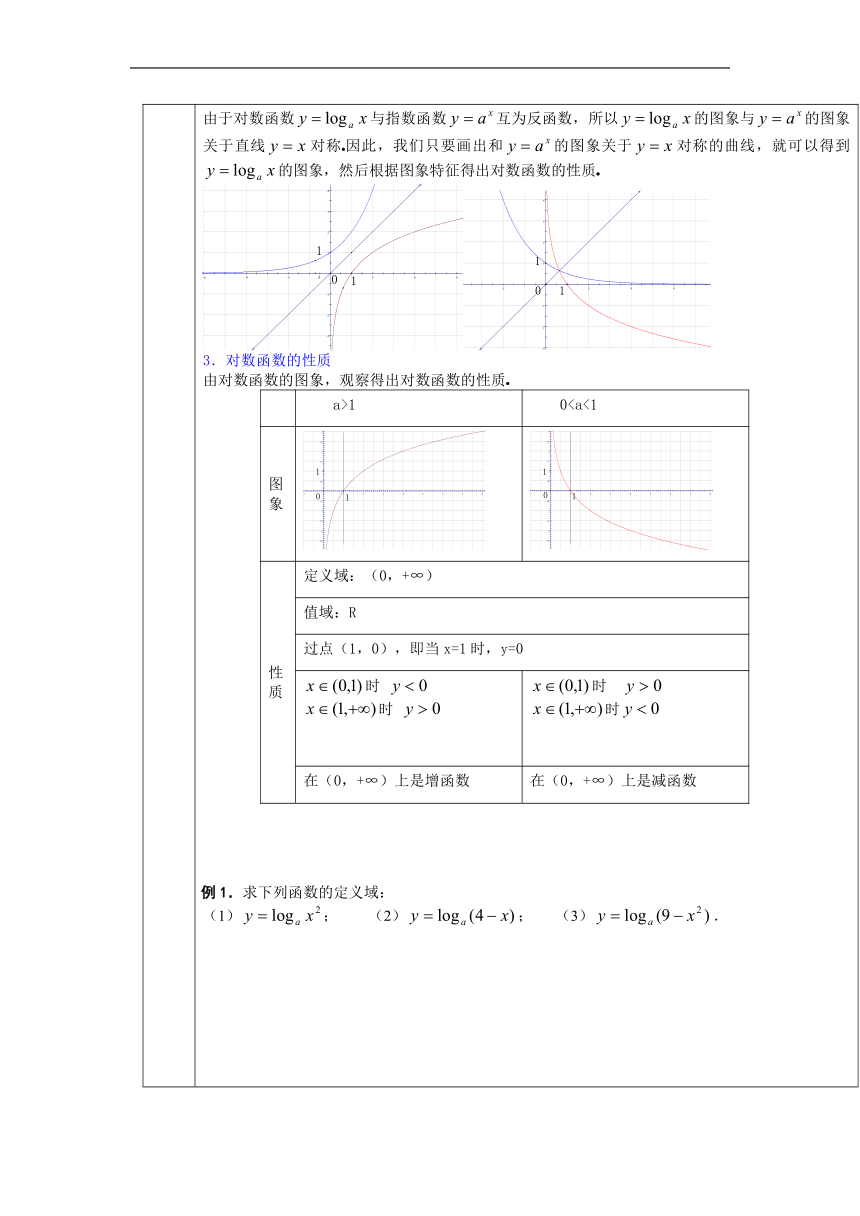
教学过程 课前检测: 1.设a=,b=,c=,则( ) A.a<c<b B.b<c<a C.a<b<c D.b<a<c 2.已知a>0且a≠1,则函数y=ax与y=loga(-x)的图象可能是( ) 3.函数y=log2x在[1,2]上的值域是( ) A.R B.[0,+∞) C.(-∞,1] D.[0,1] 4.函数y=的定义域是________. 5.求函数的单调区间 1.对数函数的定义: 函数叫做对数函数;它是指数函数 的反函数对数函数 的定义域为,值域为 2.对数函数的图象 由于对数函数与指数函数互为反函数,所以的图象与的图象关于直线对称因此,我们只要画出和的图象关于对称的曲线,就可以得到的图象,然后根据图象特征得出对数函数的性质 3.对数函数的性质 由对数函数的图象,观察得出对数函数的性质 a>10例1.求下列函数的定义域: (1); (2); (3). 例2.求函数和函数的反函数。 例3.比较下列各组数中两个值的大小: (1),; (2),; (3),. 例4.比较下列比较下列各组数中两个值的大小: (1),; (2),; (3),,; (4),,. 例5.已知,比较,的大小。 例6.求下列函数的值域: ;(2); (3)(且). 例7.判断函数的奇偶性。 例8.求函数的单调区间。 例9.若函数在区间上是增函数,的取值范围。
课后作业 1.如果点P(lga,lgb)关于x轴的对称点的坐标是(0,-1),则a和b的值是( ) A.a=1,b=10 B.a=1,b= C.a=10,b=1 D.a=,b=1 2.与函数y=10lg(x-1)的图像相同的函数是( ) A.y=x-1 B.y=|x-1| C.y= D.y= 3.函数y=lg(2-x)的定义域是 ( ) A.(-∞,2) B. (-∞,2] C.(2,+∞) D. [2,+∞) 4. 三个数的大小关系为 ( ) A B C D 5.函数的定义域为[1,2],则函数的定义域为 A.[0,1] B.[1,2] C.[2,4] D.[4,16] 6.函数的定义域是 ( ) A B C D 7. 已知函数 ( ) A B C D 8.求函数的单调递增区间, 9.已知函数, 求:(1)f(x)的定义域 (2)能使f(x)>0成立的x的取值范围 10.对于函数,解答下述问题: (1)若函数的定义域为R,求实数a的取值范围; (2)若函数的值域为R,求实数a的取值范围;
课 后 记 本节课教学计划完成情况:照常完成□ 提前完成□ 延后完成□ 学生的接受程度:完全能接受□ 部分能接受□ 不能接受□ 学生的课堂表现:很积极□ 比较积极□ 一般□ 不积极□ 学生上次的作业完成情况:数量 % 完成质量 分 存在问题
备注
班主任签字 家长或学生签字 教研主任审批
学科 数 学 年级 高一 教材版本 人教版
阶段 第( )周 观察期:□ 维护期:□
课题名称 对数函数 课时计划 第( )次课 共 ( )课时 上课时间
教学目标 掌握对数函数的基本性质 能够理解对数函数的应用
教学重点 对数函数图像特征和性质
教学难点 对数函数与其他函数复合时的性质
教学过程 课前检测: 1.设a=,b=,c=,则( ) A.a<c<b B.b<c<a C.a<b<c D.b<a<c 2.已知a>0且a≠1,则函数y=ax与y=loga(-x)的图象可能是( ) 3.函数y=log2x在[1,2]上的值域是( ) A.R B.[0,+∞) C.(-∞,1] D.[0,1] 4.函数y=的定义域是________. 5.求函数的单调区间 1.对数函数的定义: 函数叫做对数函数;它是指数函数 的反函数对数函数 的定义域为,值域为 2.对数函数的图象 由于对数函数与指数函数互为反函数,所以的图象与的图象关于直线对称因此,我们只要画出和的图象关于对称的曲线,就可以得到的图象,然后根据图象特征得出对数函数的性质 3.对数函数的性质 由对数函数的图象,观察得出对数函数的性质 a>10
课后作业 1.如果点P(lga,lgb)关于x轴的对称点的坐标是(0,-1),则a和b的值是( ) A.a=1,b=10 B.a=1,b= C.a=10,b=1 D.a=,b=1 2.与函数y=10lg(x-1)的图像相同的函数是( ) A.y=x-1 B.y=|x-1| C.y= D.y= 3.函数y=lg(2-x)的定义域是 ( ) A.(-∞,2) B. (-∞,2] C.(2,+∞) D. [2,+∞) 4. 三个数的大小关系为 ( ) A B C D 5.函数的定义域为[1,2],则函数的定义域为 A.[0,1] B.[1,2] C.[2,4] D.[4,16] 6.函数的定义域是 ( ) A B C D 7. 已知函数 ( ) A B C D 8.求函数的单调递增区间, 9.已知函数, 求:(1)f(x)的定义域 (2)能使f(x)>0成立的x的取值范围 10.对于函数,解答下述问题: (1)若函数的定义域为R,求实数a的取值范围; (2)若函数的值域为R,求实数a的取值范围;
课 后 记 本节课教学计划完成情况:照常完成□ 提前完成□ 延后完成□ 学生的接受程度:完全能接受□ 部分能接受□ 不能接受□ 学生的课堂表现:很积极□ 比较积极□ 一般□ 不积极□ 学生上次的作业完成情况:数量 % 完成质量 分 存在问题
备注
班主任签字 家长或学生签字 教研主任审批
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
