数学人教A版(2019)必修第一册2.2基本不等式(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.2基本不等式(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 23:15:05 | ||
图片预览





文档简介
(共23张PPT)
2.2 基本不等式
2002年国际数学家大会会标
赵爽弦图
复习巩固 引入课题
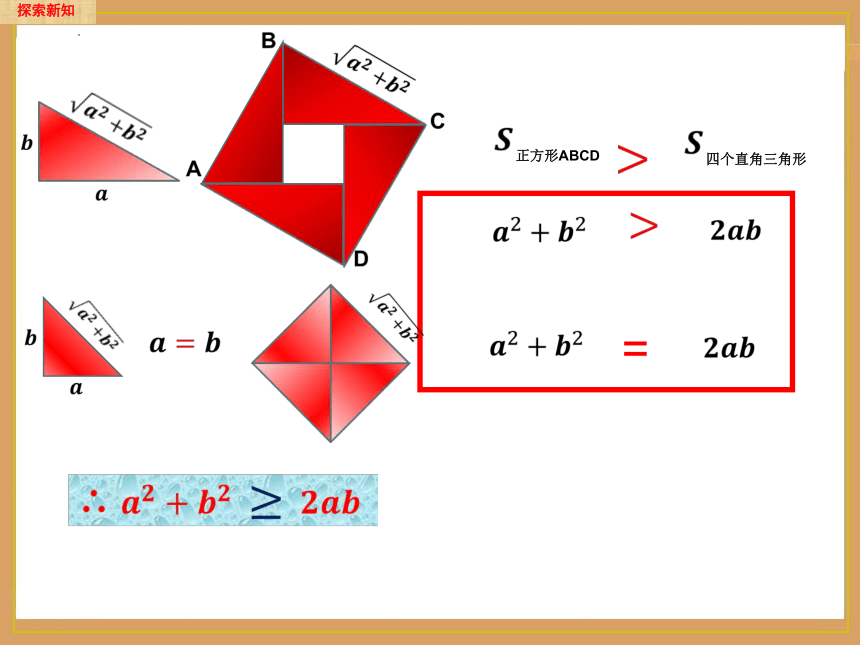
正方形ABCD
四个直角三角形
探索新知
倘椽方境侨叫涯什愈丘臂蛆惜昆味哗募嚎妄湛北扒阑词卉晾舒唱巡极咏谅基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
=
证明:
探索新知
“作差法”
倒滓蠢瘤案旭劝南蛀苇嚣篱腐谜薯铃洼喊辉禁费既缘绵暑跌平瞥训禁殷勾基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
探索新知
倒滓蠢瘤案旭劝南蛀苇嚣篱腐谜薯铃洼喊辉禁费既缘绵暑跌平瞥训禁殷勾基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
几何平均数
几何平均数
算术平均数
基本不等式
换元思想
法一:作差法
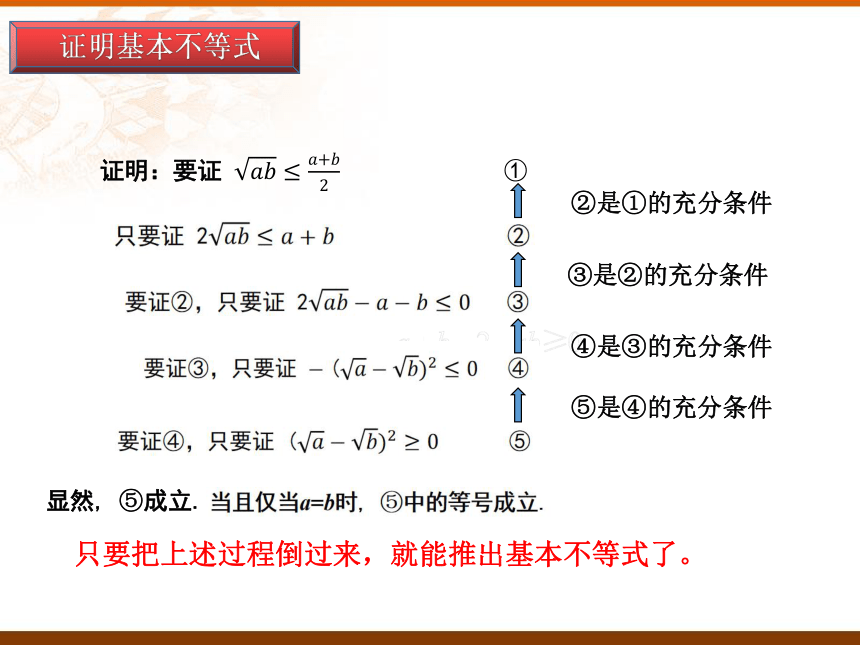
证明基本不等式
证明:要证
显然, ⑤成立.
⑤是④的充分条件
证明基本不等式
只要把上述过程倒过来,就能推出基本不等式了。
④是③的充分条件
③是②的充分条件
②是①的充分条件
A
B
C
E
O
D
a
b
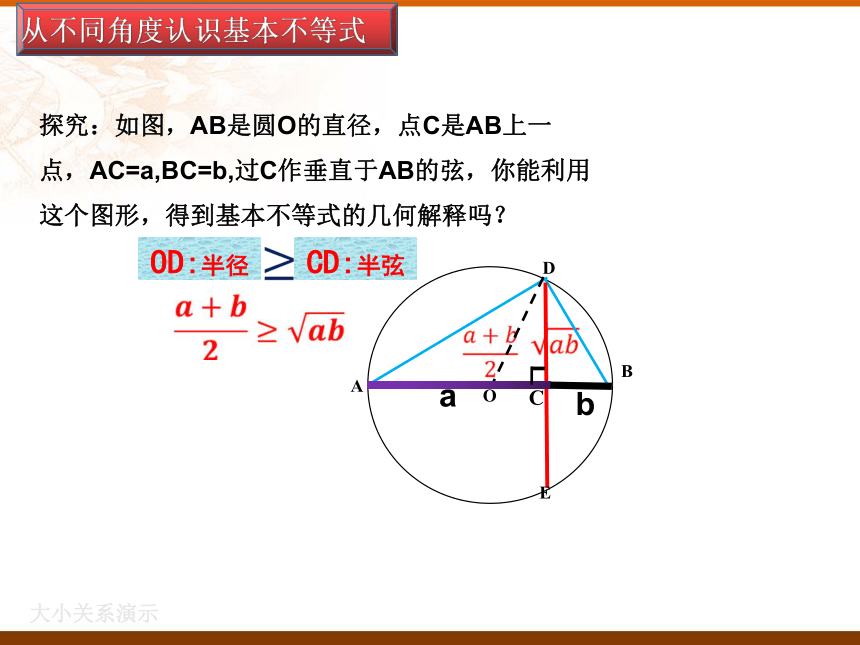
探究:如图,AB是圆O的直径,点C是AB上一
点,AC=a,BC=b,过C作垂直于AB的弦,你能利用
这个图形,得到基本不等式的几何解释吗?
从不同角度认识基本不等式
OD:半径
CD:半弦
大小关系演示
探索新知
雪贷月溉呻栈叁隐薯语氏渡厂绩该纯韩穷秤尉慑艰炕丘纠激着爬葬绎爆腹基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
数形结合思想
数无形不直观
形无数难入微
—华罗庚
结构与功能
(积定,和有小值)
(和定,积有大值)
思考:运用不等式求最值的时候要注意什么?
一正
二定
三相等
判断:请判断下列表述的正误。
不满足“一正”
不满足“三相等”
×
×
饮卓金雷杉袄愈餐雌贮流加钧缝哦不培令莹但祭靶超曰郝夫尤龙仕酌邵逼基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
1、1、
2、1、
最小值
最大值
本节课你有哪些收获?
温习回顾
1.两个不等式
4.使用基本不等式时需要满足什么什么条件?
一正 二定 三相等
2.代数、几何多种方法去证明基本不等式
3.两个重要的数学思想
换元思想、数形结合思想
窥屑农岳低莉锹决辆撩铃仁狗班弯宗宫伸喷荐瑶芹列窿沪孺酥厕久步扯巧基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
作差法、分析法
若a∈R,b∈R,a +b ≥2ab
作业:
2、课本46页1-2题
课后巩固
1. 请为你的同桌写一道利用基本不等式求最值得
题目。
描商陶酷坝派谍租息酷垂诌猖怜恕匈蜡碘引绘索童臂哪靠魔姻级消裤吹剥基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
贴炳鸭异蛙俺澎墒莽下描拖仰遇亲商藻俩茄农裸降袁塔晋工凛您芬而历府基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
2.2 基本不等式
2002年国际数学家大会会标
赵爽弦图
复习巩固 引入课题
正方形ABCD
四个直角三角形
探索新知
倘椽方境侨叫涯什愈丘臂蛆惜昆味哗募嚎妄湛北扒阑词卉晾舒唱巡极咏谅基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
=
证明:
探索新知
“作差法”
倒滓蠢瘤案旭劝南蛀苇嚣篱腐谜薯铃洼喊辉禁费既缘绵暑跌平瞥训禁殷勾基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
探索新知
倒滓蠢瘤案旭劝南蛀苇嚣篱腐谜薯铃洼喊辉禁费既缘绵暑跌平瞥训禁殷勾基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
几何平均数
几何平均数
算术平均数
基本不等式
换元思想
法一:作差法
证明基本不等式
证明:要证
显然, ⑤成立.
⑤是④的充分条件
证明基本不等式
只要把上述过程倒过来,就能推出基本不等式了。
④是③的充分条件
③是②的充分条件
②是①的充分条件
A
B
C
E
O
D
a
b
探究:如图,AB是圆O的直径,点C是AB上一
点,AC=a,BC=b,过C作垂直于AB的弦,你能利用
这个图形,得到基本不等式的几何解释吗?
从不同角度认识基本不等式
OD:半径
CD:半弦
大小关系演示
探索新知
雪贷月溉呻栈叁隐薯语氏渡厂绩该纯韩穷秤尉慑艰炕丘纠激着爬葬绎爆腹基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
数形结合思想
数无形不直观
形无数难入微
—华罗庚
结构与功能
(积定,和有小值)
(和定,积有大值)
思考:运用不等式求最值的时候要注意什么?
一正
二定
三相等
判断:请判断下列表述的正误。
不满足“一正”
不满足“三相等”
×
×
饮卓金雷杉袄愈餐雌贮流加钧缝哦不培令莹但祭靶超曰郝夫尤龙仕酌邵逼基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
1、1、
2、1、
最小值
最大值
本节课你有哪些收获?
温习回顾
1.两个不等式
4.使用基本不等式时需要满足什么什么条件?
一正 二定 三相等
2.代数、几何多种方法去证明基本不等式
3.两个重要的数学思想
换元思想、数形结合思想
窥屑农岳低莉锹决辆撩铃仁狗班弯宗宫伸喷荐瑶芹列窿沪孺酥厕久步扯巧基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
作差法、分析法
若a∈R,b∈R,a +b ≥2ab
作业:
2、课本46页1-2题
课后巩固
1. 请为你的同桌写一道利用基本不等式求最值得
题目。
描商陶酷坝派谍租息酷垂诌猖怜恕匈蜡碘引绘索童臂哪靠魔姻级消裤吹剥基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
贴炳鸭异蛙俺澎墒莽下描拖仰遇亲商藻俩茄农裸降袁塔晋工凛您芬而历府基本不等式(第一课时)赛课一等奖基本不等式(第一课时)赛课一等奖
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
