九年级人教版数学上册 25.3 用频率估计概率 课时练习-2022-2023学年(含解析)
文档属性
| 名称 | 九年级人教版数学上册 25.3 用频率估计概率 课时练习-2022-2023学年(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 07:14:50 | ||
图片预览




文档简介
25.3 用频率估计概率(附解析)
一、单选题(共10个小题)
1.某校生物兴趣小组为了解种子发芽情况,重复做了大量种子发芽的实验,结果如下:
实验种子的数量n 100 200 500 1000 5000 10000
发芽种子的数量m 98 182 485 900 4750 9500
种子发芽的频率 0.98 0.91 0.97 0.90 0.95 0.95
根据以上数据,估计该种子发芽的概率是( )
A.0.90 B.0.98 C.0.95 D.0.91
2.某实验小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小刚随机出的是“石头”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽取一张牌的花色是方块
C.布袋中有1个红球和2个黄球,它们只是颜色上有区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的点数是4
3.在数学活动课上,张明运用统计方法估计瓶子中的豆子的数量.他先取出粒豆子,给这些豆子做上记号,然后放回瓶子中,充分摇匀之后再取出粒豆子,发现其中粒有刚才做的记号,利用得到的数据可以估计瓶子中豆子的数量约为( )粒.
A. B. C. D.
4.在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.4左右,则袋中白球约有( )
A.5个 B.10个 C.15个 D.25个
5.在一个不透明的口袋中,放置6个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值是( )
A.2 B.3 C.5 D.8
6.下列叙述不正确的是( )
A.某种彩票中奖的概率为1%,那么买100张这种彩票一定会中奖
B.掷一枚骰子,向上的一面出现的点数为4是随机事件
C.某兴趣小组14位同学中至少两人的生日在同一月份是必然事件
D.在相同条件下,试验的次数足够大时,某一随机事件发生的频率会稳定于某一数值
7.掷一枚质地均匀的硬币,硬币落地后,会出现如图1的两种情况.
图2是计算机模拟抛掷一枚硬币试验的折线图.下面判断正确的是( )
A.当抛掷的次数为300次时,正面朝上的次数大于200次
B.当抛掷的次数为500次时,记录数据为0.48,所以随机掷一枚硬币“正面朝上”的概率为0.48
C.当抛掷的次数在2000次以上时,“正面朝上”的频率总在0.5附近摆动,显示出频率的稳定性,由此可估计随机掷一枚硬币“正面朝上”的概率为0.5
D.当抛掷次数大于3000次时,随机掷一枚硬币“正面朝上”的频率一定为0.5
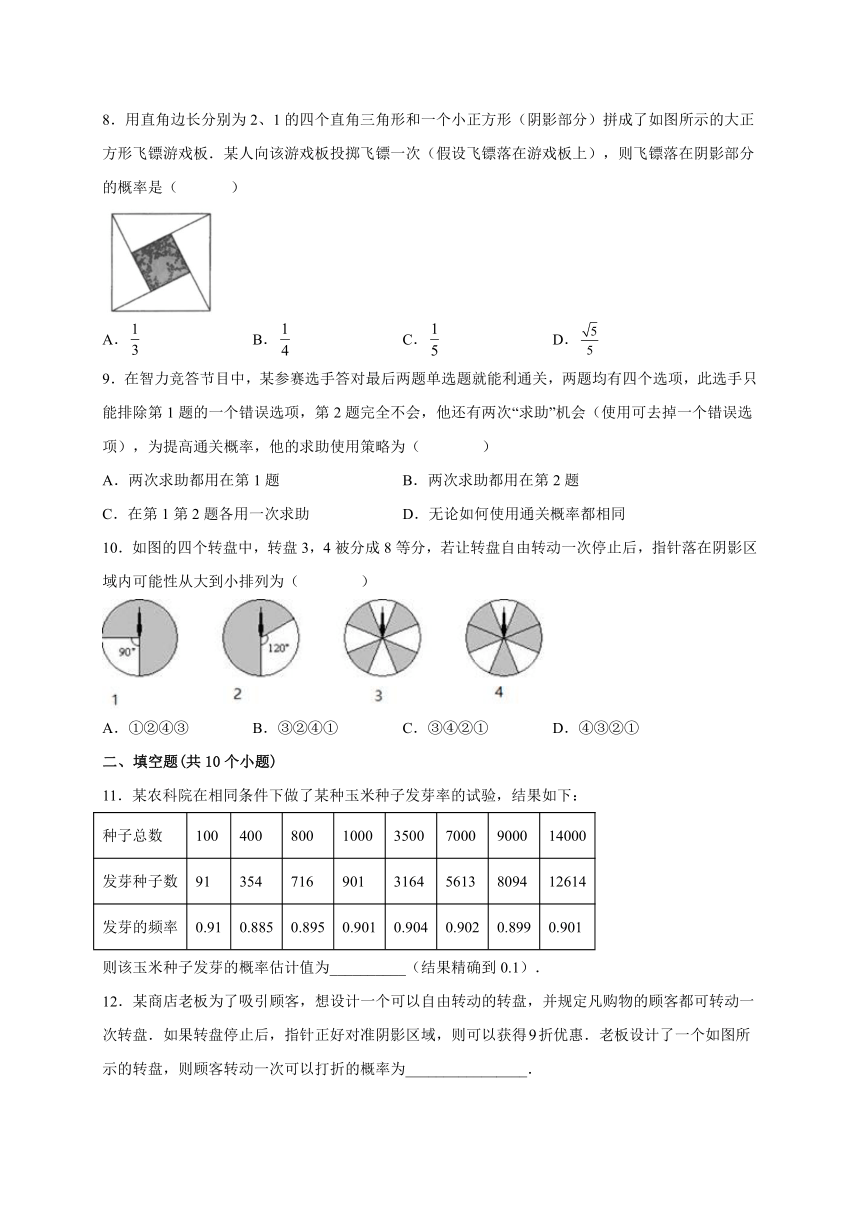
8.用直角边长分别为2、1的四个直角三角形和一个小正方形(阴影部分)拼成了如图所示的大正方形飞镖游戏板.某人向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )
A. B. C. D.
9.在智力竞答节目中,某参赛选手答对最后两题单选题就能利通关,两题均有四个选项,此选手只能排除第1题的一个错误选项,第2题完全不会,他还有两次“求助”机会(使用可去掉一个错误选项),为提高通关概率,他的求助使用策略为( )
A.两次求助都用在第1题 B.两次求助都用在第2题
C.在第1第2题各用一次求助 D.无论如何使用通关概率都相同
10.如图的四个转盘中,转盘3,4被分成8等分,若让转盘自由转动一次停止后,指针落在阴影区域内可能性从大到小排列为( )
A.①②④③ B.③②④① C.③④②① D.④③②①
二、填空题(共10个小题)
11.某农科院在相同条件下做了某种玉米种子发芽率的试验,结果如下:
种子总数 100 400 800 1000 3500 7000 9000 14000
发芽种子数 91 354 716 901 3164 5613 8094 12614
发芽的频率 0.91 0.885 0.895 0.901 0.904 0.902 0.899 0.901
则该玉米种子发芽的概率估计值为__________(结果精确到0.1).
12.某商店老板为了吸引顾客,想设计一个可以自由转动的转盘,并规定凡购物的顾客都可转动一次转盘.如果转盘停止后,指针正好对准阴影区域,则可以获得折优惠.老板设计了一个如图所示的转盘,则顾客转动一次可以打折的概率为________________.
13.下列语句中,关于频率与概率的关系表示正确的有___________.
①频率就是概率
②频率是客观存在的,与试验次数无关
③随着试验次数的增加,频率一般会越来越接近概率
④概率是随机的,在实验前不能确定
14.在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,利用计算机模拟的结果,摸出黑球的频率在0.5附近波动,由此可以估计出n的值是_________.
15.一批电子产品的抽样合格率为75%,当购买该电子产品足够多时,平均来说,购买__________个这样的电子产品,可能会出现1个次品.
16.八年级的小亮和小明是好朋友,他们都报名参加学校的田径运动会,将被教练随机分进甲、乙、丙三个训练队,他俩被分进同一训练队的概率是__.
17.某船队要对下月是否出海作出决策,若出海后是好天气,可得收益5000元;若出海后天气变坏,将要损失2000元;若不出海,无论天气好坏都要承担1000元的损失费,船队队长通过上网查询下月的天气情况后,预测下月好天气的机会是,坏天气的机会是,则作出决策为________(填“出海”、“不出海”).
18.已知数据:,,,,0,其中无理数出现的频率为_________.
19.某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为___________.
20.有五张正面分别写有数字-4,-3,0,2,3的卡片,五张卡片除了数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为,则抽取的既能使关于的方程有实数根,又能使以为自变量的二次函数,当时,随的增大而减小的概率为___________.
三、解答题(共6个小题)
21.牛牛元旦那天和爸爸、妈妈一起回老家看望爷爷、奶奶.因为期末考试将至,他把书包也带了去,准备抽空看看书.书包内有语文、数学、英语、物理四本课本.他想通过实验的方法了解从书包中任意取出一本书,刚好是数学课本的机会有多大.于是他把四本课本的顺序打乱后,闭上眼睛从书包中任取一本书,记录结果后将书放回书包后,再重复上面的做法,得到了下表中的数据
取书次数 40 80 120 160 200 240 280 320 360 400
取中数学课本的频数 8 22 29 42 51 59 70 81 89 102
取中数学课本的频率
(1)请根据表中提供的数据,求出取中数学课本的频率(精确到;
(2)根据统计表在图中画出折线统计图;
(3)从统计图中你发现了什么?
(4)你还能用别的替代物进行模拟实验吗?请说出一种方法.
22.在一个不透明的盒子里装有黑、白两种颜色的球,这些球除颜色外都相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的部分统计数据:
摸球的次数n 10 20 50 100 200 400 500 1000 2000
摸到白球的次数m 4 7 10 28 45 97 127 252 498
摸到白球的频率 0.400 0.350 0.200 0.280 0.225 0.243 0.254 0.252 0.249
(1)摸到白球的概率的估计值是多少?请说明理由.(精确到0.01)
(2)某小组进行“用频率估计概率”的试验,符合(1)中结果的试验最有可能的是 (填序号).
①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上.
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲.
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数“小于3”.
23.在一个不透明的盒子里装有红、黑两种颜色的球共20个,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,我们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数n 50 100 300 500 800 1000 2000
摸到红球的次数m 14 33 95 155 241 298 602
摸到红球的频率 0.28 0.33 0.317 0.31 0.301 0.298 0.301
(1)通过以上实验,摸到红球的概率估计为____(精确到0.1) ,盒子里红球的数量为____个.
(2)若先从袋子中取出个红球,再从袋子中随机摸出1个球,若“摸出黑球”为必然事件,则___.
(3)若先从袋子中取出个红球,再放入个一样的黑球并摇匀,随机摸出1个红球的概率为,求的值.
24.某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 50 100 200 300 400 500
次品件数 0 4 14 19 24 30
(1)求从这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换
25.如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明设计了一个如下方法:
①在此封闭图形内画出一个半径为1米的圆.
②在此封闭图形旁边闭上眼晴向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 50 150 300 500 …
小石子落在圆内(含圆上)的次数m 20 59 123 203 …
小石子落在圆外的阴影部分(含外缘)的次数n 29 91 176 293 …
m∶n 0.689 0.694 0.689 0.706
(1)通过以上信息,可以发现当投掷的次数很大时,则m∶n的值越来越接近 (结果精确到0.1).
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1).
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留)
26.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶以每瓶2元的价格当天全部降价处理完.根据往年销售经验,每天需求量与当天本地最高气温有关.为了制定今年六月份的订购计划,计划部对去年六月份每天的最高气温x(℃)及当天售出(不含降价处理)的酸奶瓶数),等数据统计如下:
x(℃) 15≤x<20 20≤x<25 25≤x<30 30≤x≤35
天数 6 10 11 3
y(瓶) 270 330 360 420
以最高气温位于各范围的频率代替最高气温位于该范围的概率.
(1)试估计今年六月份每天售出(不含降价处理)的酸奶瓶数不高于360瓶的概率;
(2)根据供货方的要求,今年这种酸奶每天的进货量必须为100的整数倍.问今年六月份这种酸奶一天的进货量为多少时,平均每天销售这种酸奶的利润最大?
参考答案:
1.C
【详解】解:∵随着种子数量的增多,其发芽的频率逐渐稳定在0.95,
∴估计该种子发芽的概率是0.95,
故选: C.
2.D
【详解】解:A.在“石头、剪刀、布”的游戏中,小刚随机出的是“剪刀”的概率是,不符合题意;
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是,不符合题意;
C.布袋中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是红球的概率是,不符合题意;
D.掷一个质地均匀的正六面体骰子,向上的面点数是4的概率是,符合题意;
故选:D.
3.B
【详解】设瓶子中有豆子粒豆子,
根据题意得:,
解得:,
经检验:是原分式方程的解,
答:估计瓶子中豆子的数量约为粒.
故选:.
4.B
【详解】解:经过多次重复试验,发现摸到白球的频率稳定在0.4左右,
摸到红球的频率稳定在0.6左右,
袋中装有若干个白球和15个红球,
袋中球的总数为:,
袋中白球约有:(个,
故选:B.
5.B
【详解】解:由图可知,经过大量实验发现,黄球出现的频率稳定在0.6附近,
∴
解得 n=3
故选:B.
6.A
【详解】解:A.某种彩票中奖的概率为1%,那么买100张这种彩票不一定会中奖,此选项表述错误,符合题意;
B.掷一枚骰子,向上的一面出现的点数为4是随机事件,正确,不符合题意;
C.某兴趣小组14位同学中至少两人的生日在同一月份是必然事件,正确,不符合题意;
D.在相同条件下,试验的次数足够大时,某一随机事件发生的频率会稳定于某一数值,正确,不符合题意;
故选:A.
7.C
【详解】根据图象可知当抛掷的次数为300次时,正面朝上的频率为0.5,
A.∴此次试验正面朝上的次数为300×0.5=150(次)<200次,故A错误;
B.随机掷一枚硬币“正面朝上”的概率与抛掷的次数无关,故B错误;
C.根据在同样条件下,大量重复试验时,一个随机事件发生的频率逐渐稳定到一个稳定值时,这个稳定的频率的值可以作为这个事件发生的概率,故C正确;
D.随机掷一枚硬币“正面朝上”的概率与抛掷的次数无关,故D错误;
故选C.
8.C
【详解】解:大正方形的面积为:,
阴影部分的小正方形的面积为:,
∴飞镖落在阴影部分的概率是,
故选:C.
9.A
【详解】解:①若两次求助都用在第1题,
根据题意可知,第1题肯定能答对,第2题答对的概率为
故此时该选手通关的概率为:;
②若在第1第2题各用一次求助,
画树状图如下:上层A、B表示第一题剩下的两个选项,下层A、B、C表示第二题剩下的三个选项,
共有6种等可能的结果,其中该选手通关的可能只有1种,故此时该选手通关的概率为:;
③两次求助都用在第2题
画树状图如下:上层A、B、C表示第一题剩下的三个选项,下层A、B表示第二题剩下的二个选项,
共有6种等可能的结果,其中该选手通关的可能只有1种,故此时该选手通关的概率为:.
∵>
∴两次求助都用在第1题,该选手通关的概率大,
故选A.
10.A
【详解】解:图1阴影部分为270°,图2阴影部分为240°,图3每份为45°,阴影部分共4份为180°,图4每份为45°阴影部分共5份为225°,所以①②④③,
故选A.
11.0.9
【详解】解:∵观察表格,发现大量重复试验发芽的频率逐渐稳定在0.9左右,
∴该玉米种子发芽的概率为0.9,
故答案为:0.9.
12.
【详解】∵,
∴阴影部分面积占总面积的,即:顾客转动一次可以打折的概率为.
故答案是:.
13.③
【详解】解:①:频率不是概率,频率会随着重复试验的次数变化而变化,而概率是固定的,故①错误;
②:频率是客观存在的,与试验次数有关,试验次数越多,频率越稳定,故②错误
③:由频率的性质知:随着试验次数的增加,事件发生的频率一般会稳定于概率,故③正确;
④:概率是客观的,在试验前能确定,故④错误.
故答案为:③.
14.10
【详解】解:由题意可得,,
解得,n=10.
经检验,n=10是原方程的根,
故估计n的值为10.
故答案为:10.
15.4
【详解】解:∵产品的抽样合格率为,
∴产品的抽样不合格率为
∴当购买该电子产品足够多时,平均来说,每购4个这样的电子产品,就可能会出现1个次品
故答案为:4.
16.
【详解】解:假设小亮在甲,则小明有甲、乙、丙三种,那么他们要在同一队的可能只有,同理,小亮在乙或丙,他们要在同一队的可能也只有.
17.出海
【详解】解:预测下月好天气的机会是,坏天气的机会是,,
下月是好天气的可能性坏天气的可能性;
又若出海后是好天气,可得收益5000元;若出海后天气变坏,将要损失2000元;若不出海,无论天气好坏都要承担1000元的损失费,
出海的话,获得平均收益(获得收益的数学期望)(元,
不出海:(元,
,
船队队长作出决策为:出海.
故答案为:出海.
18.
【详解】解:在数据,,,,0中,无理数有3个,
∴无理数出现的频率为,
故答案为:.
19.0.5
【详解】解:∵捕捞到鲫鱼的频率稳定在0.25左右,
设鲫鱼的条数为x,可得:
;
解得:x=500,
经检验:x=500是原方程的解且符合实际意义
∴由题意可得,捞到草鱼的概率约为:
,
故答案为:0.5.
20.
【详解】有实数根,
,
∴,
,
又,
对称轴为:,
时,随增大而减小,
,
综上,
可取0,2,
∴,
故答案为:.
21.(1)0.250;(2)见解析;(3)见解析;(4)能,用扑克牌,每一种只取一张,即能替代
【详解】(1)
解:;
;
;
;
;
;
;
;
;
;
(2)
统计图如图
(3)
解:取中数学课本的频率随着取书次数的增加,越来越接近0.25
(4)
能,用扑克牌,每一种只取一张,即能替代.
【点睛】本题主要考查利用频率估算概率的方法,按照步骤解题即可.
22.(1)0.25,理由见解析;(2)②
【详解】(1)
解:摸到白球的概率的估计值是0.25;
理由:大量重复实验下,摸到白球的频率稳定在0.25附近,0.25即概率的估计值;
(2)
解:①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上的概率是;
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲的概率是=0.25;
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数“小于3”的概率是=;
综上所述,符合(1)中结果的试验最有可能的是②,
故答案为:②.
23.(1)0.3,6;(2)6;(3)1
【详解】(1)
解:通过以上实验,摸到红球的概率估计为0.3,
20×0.3=6;
故答案为:0.3,6
(2)
解:因为“摸出黑球”为必然事件,
∴袋子只有黑球,
∴需要拿出所有的红球,即x=6;
故答案为:6
(3)
解:由(1)知红球6个,黑球14个,
拿掉x个红球,加入x个黑球后,则红球(6-x),依题意得:
,
解得x=1,
故红球取出1个.
24.(1);(2)36
【详解】(1)
解:抽查总体数m=50+100+200+300+400+500=1550,
次品件数n=0+4+14+19+24+30=91,
这批衬衣中任抽1件是次品的概率为.
(2)
根据(1)的结论:这批衬衣中任抽1件是次品的概率为0.06,
则600×0.06=36(件).
答:准备36件正品衬衣供顾客调换.
25.(1)0.7;(2)0.4;(3)封闭图形的面积为10π平方米.
【详解】(1)
解:20÷29≈0.69;
59÷91≈0.65;
123÷176≈0.70,
…
当投掷的次数很大时,则m:n的值越来越接近0.7;
故答案为:0.7;
(2)
解:观察表格得:随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在0.4,
故答案为:0.4;
(3)
解:设封闭图形的面积为a,根据题意得:=0.4,
解得:a=10π,
答:封闭图形的面积为10π平方米.
26.(1)0.9;(2)瓶
【详解】解:(1)依题意可知,
今年六月份每月售出(不含降价处理)的酸奶瓶数不高于瓶的概率为;
(2)根据题意可知:
该超市当天售出一瓶酸奶可获利元,降级处理一瓶亏元,
设今年六月销售这种酸奶每天的进货量为瓶,平均每天的利润为元,则:
当时,
,
当时,
,
当时,
,
当时,
,
当时,与时比较,
六月增订的部分,亏本售出的比正常售出的多,
所以其每天的平均利润比时平均每天利润少.
综上所述:时,的值达到最大.
即今年六月份这种酸奶一年的进货量为瓶时,平均每天销售这种酸奶的利润最大.
一、单选题(共10个小题)
1.某校生物兴趣小组为了解种子发芽情况,重复做了大量种子发芽的实验,结果如下:
实验种子的数量n 100 200 500 1000 5000 10000
发芽种子的数量m 98 182 485 900 4750 9500
种子发芽的频率 0.98 0.91 0.97 0.90 0.95 0.95
根据以上数据,估计该种子发芽的概率是( )
A.0.90 B.0.98 C.0.95 D.0.91
2.某实验小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小刚随机出的是“石头”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽取一张牌的花色是方块
C.布袋中有1个红球和2个黄球,它们只是颜色上有区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的点数是4
3.在数学活动课上,张明运用统计方法估计瓶子中的豆子的数量.他先取出粒豆子,给这些豆子做上记号,然后放回瓶子中,充分摇匀之后再取出粒豆子,发现其中粒有刚才做的记号,利用得到的数据可以估计瓶子中豆子的数量约为( )粒.
A. B. C. D.
4.在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.4左右,则袋中白球约有( )
A.5个 B.10个 C.15个 D.25个
5.在一个不透明的口袋中,放置6个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值是( )
A.2 B.3 C.5 D.8
6.下列叙述不正确的是( )
A.某种彩票中奖的概率为1%,那么买100张这种彩票一定会中奖
B.掷一枚骰子,向上的一面出现的点数为4是随机事件
C.某兴趣小组14位同学中至少两人的生日在同一月份是必然事件
D.在相同条件下,试验的次数足够大时,某一随机事件发生的频率会稳定于某一数值
7.掷一枚质地均匀的硬币,硬币落地后,会出现如图1的两种情况.
图2是计算机模拟抛掷一枚硬币试验的折线图.下面判断正确的是( )
A.当抛掷的次数为300次时,正面朝上的次数大于200次
B.当抛掷的次数为500次时,记录数据为0.48,所以随机掷一枚硬币“正面朝上”的概率为0.48
C.当抛掷的次数在2000次以上时,“正面朝上”的频率总在0.5附近摆动,显示出频率的稳定性,由此可估计随机掷一枚硬币“正面朝上”的概率为0.5
D.当抛掷次数大于3000次时,随机掷一枚硬币“正面朝上”的频率一定为0.5
8.用直角边长分别为2、1的四个直角三角形和一个小正方形(阴影部分)拼成了如图所示的大正方形飞镖游戏板.某人向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )
A. B. C. D.
9.在智力竞答节目中,某参赛选手答对最后两题单选题就能利通关,两题均有四个选项,此选手只能排除第1题的一个错误选项,第2题完全不会,他还有两次“求助”机会(使用可去掉一个错误选项),为提高通关概率,他的求助使用策略为( )
A.两次求助都用在第1题 B.两次求助都用在第2题
C.在第1第2题各用一次求助 D.无论如何使用通关概率都相同
10.如图的四个转盘中,转盘3,4被分成8等分,若让转盘自由转动一次停止后,指针落在阴影区域内可能性从大到小排列为( )
A.①②④③ B.③②④① C.③④②① D.④③②①
二、填空题(共10个小题)
11.某农科院在相同条件下做了某种玉米种子发芽率的试验,结果如下:
种子总数 100 400 800 1000 3500 7000 9000 14000
发芽种子数 91 354 716 901 3164 5613 8094 12614
发芽的频率 0.91 0.885 0.895 0.901 0.904 0.902 0.899 0.901
则该玉米种子发芽的概率估计值为__________(结果精确到0.1).
12.某商店老板为了吸引顾客,想设计一个可以自由转动的转盘,并规定凡购物的顾客都可转动一次转盘.如果转盘停止后,指针正好对准阴影区域,则可以获得折优惠.老板设计了一个如图所示的转盘,则顾客转动一次可以打折的概率为________________.
13.下列语句中,关于频率与概率的关系表示正确的有___________.
①频率就是概率
②频率是客观存在的,与试验次数无关
③随着试验次数的增加,频率一般会越来越接近概率
④概率是随机的,在实验前不能确定
14.在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,利用计算机模拟的结果,摸出黑球的频率在0.5附近波动,由此可以估计出n的值是_________.
15.一批电子产品的抽样合格率为75%,当购买该电子产品足够多时,平均来说,购买__________个这样的电子产品,可能会出现1个次品.
16.八年级的小亮和小明是好朋友,他们都报名参加学校的田径运动会,将被教练随机分进甲、乙、丙三个训练队,他俩被分进同一训练队的概率是__.
17.某船队要对下月是否出海作出决策,若出海后是好天气,可得收益5000元;若出海后天气变坏,将要损失2000元;若不出海,无论天气好坏都要承担1000元的损失费,船队队长通过上网查询下月的天气情况后,预测下月好天气的机会是,坏天气的机会是,则作出决策为________(填“出海”、“不出海”).
18.已知数据:,,,,0,其中无理数出现的频率为_________.
19.某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为___________.
20.有五张正面分别写有数字-4,-3,0,2,3的卡片,五张卡片除了数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为,则抽取的既能使关于的方程有实数根,又能使以为自变量的二次函数,当时,随的增大而减小的概率为___________.
三、解答题(共6个小题)
21.牛牛元旦那天和爸爸、妈妈一起回老家看望爷爷、奶奶.因为期末考试将至,他把书包也带了去,准备抽空看看书.书包内有语文、数学、英语、物理四本课本.他想通过实验的方法了解从书包中任意取出一本书,刚好是数学课本的机会有多大.于是他把四本课本的顺序打乱后,闭上眼睛从书包中任取一本书,记录结果后将书放回书包后,再重复上面的做法,得到了下表中的数据
取书次数 40 80 120 160 200 240 280 320 360 400
取中数学课本的频数 8 22 29 42 51 59 70 81 89 102
取中数学课本的频率
(1)请根据表中提供的数据,求出取中数学课本的频率(精确到;
(2)根据统计表在图中画出折线统计图;
(3)从统计图中你发现了什么?
(4)你还能用别的替代物进行模拟实验吗?请说出一种方法.
22.在一个不透明的盒子里装有黑、白两种颜色的球,这些球除颜色外都相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的部分统计数据:
摸球的次数n 10 20 50 100 200 400 500 1000 2000
摸到白球的次数m 4 7 10 28 45 97 127 252 498
摸到白球的频率 0.400 0.350 0.200 0.280 0.225 0.243 0.254 0.252 0.249
(1)摸到白球的概率的估计值是多少?请说明理由.(精确到0.01)
(2)某小组进行“用频率估计概率”的试验,符合(1)中结果的试验最有可能的是 (填序号).
①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上.
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲.
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数“小于3”.
23.在一个不透明的盒子里装有红、黑两种颜色的球共20个,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,我们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数n 50 100 300 500 800 1000 2000
摸到红球的次数m 14 33 95 155 241 298 602
摸到红球的频率 0.28 0.33 0.317 0.31 0.301 0.298 0.301
(1)通过以上实验,摸到红球的概率估计为____(精确到0.1) ,盒子里红球的数量为____个.
(2)若先从袋子中取出个红球,再从袋子中随机摸出1个球,若“摸出黑球”为必然事件,则___.
(3)若先从袋子中取出个红球,再放入个一样的黑球并摇匀,随机摸出1个红球的概率为,求的值.
24.某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 50 100 200 300 400 500
次品件数 0 4 14 19 24 30
(1)求从这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换
25.如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明设计了一个如下方法:
①在此封闭图形内画出一个半径为1米的圆.
②在此封闭图形旁边闭上眼晴向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 50 150 300 500 …
小石子落在圆内(含圆上)的次数m 20 59 123 203 …
小石子落在圆外的阴影部分(含外缘)的次数n 29 91 176 293 …
m∶n 0.689 0.694 0.689 0.706
(1)通过以上信息,可以发现当投掷的次数很大时,则m∶n的值越来越接近 (结果精确到0.1).
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1).
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留)
26.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶以每瓶2元的价格当天全部降价处理完.根据往年销售经验,每天需求量与当天本地最高气温有关.为了制定今年六月份的订购计划,计划部对去年六月份每天的最高气温x(℃)及当天售出(不含降价处理)的酸奶瓶数),等数据统计如下:
x(℃) 15≤x<20 20≤x<25 25≤x<30 30≤x≤35
天数 6 10 11 3
y(瓶) 270 330 360 420
以最高气温位于各范围的频率代替最高气温位于该范围的概率.
(1)试估计今年六月份每天售出(不含降价处理)的酸奶瓶数不高于360瓶的概率;
(2)根据供货方的要求,今年这种酸奶每天的进货量必须为100的整数倍.问今年六月份这种酸奶一天的进货量为多少时,平均每天销售这种酸奶的利润最大?
参考答案:
1.C
【详解】解:∵随着种子数量的增多,其发芽的频率逐渐稳定在0.95,
∴估计该种子发芽的概率是0.95,
故选: C.
2.D
【详解】解:A.在“石头、剪刀、布”的游戏中,小刚随机出的是“剪刀”的概率是,不符合题意;
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是,不符合题意;
C.布袋中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是红球的概率是,不符合题意;
D.掷一个质地均匀的正六面体骰子,向上的面点数是4的概率是,符合题意;
故选:D.
3.B
【详解】设瓶子中有豆子粒豆子,
根据题意得:,
解得:,
经检验:是原分式方程的解,
答:估计瓶子中豆子的数量约为粒.
故选:.
4.B
【详解】解:经过多次重复试验,发现摸到白球的频率稳定在0.4左右,
摸到红球的频率稳定在0.6左右,
袋中装有若干个白球和15个红球,
袋中球的总数为:,
袋中白球约有:(个,
故选:B.
5.B
【详解】解:由图可知,经过大量实验发现,黄球出现的频率稳定在0.6附近,
∴
解得 n=3
故选:B.
6.A
【详解】解:A.某种彩票中奖的概率为1%,那么买100张这种彩票不一定会中奖,此选项表述错误,符合题意;
B.掷一枚骰子,向上的一面出现的点数为4是随机事件,正确,不符合题意;
C.某兴趣小组14位同学中至少两人的生日在同一月份是必然事件,正确,不符合题意;
D.在相同条件下,试验的次数足够大时,某一随机事件发生的频率会稳定于某一数值,正确,不符合题意;
故选:A.
7.C
【详解】根据图象可知当抛掷的次数为300次时,正面朝上的频率为0.5,
A.∴此次试验正面朝上的次数为300×0.5=150(次)<200次,故A错误;
B.随机掷一枚硬币“正面朝上”的概率与抛掷的次数无关,故B错误;
C.根据在同样条件下,大量重复试验时,一个随机事件发生的频率逐渐稳定到一个稳定值时,这个稳定的频率的值可以作为这个事件发生的概率,故C正确;
D.随机掷一枚硬币“正面朝上”的概率与抛掷的次数无关,故D错误;
故选C.
8.C
【详解】解:大正方形的面积为:,
阴影部分的小正方形的面积为:,
∴飞镖落在阴影部分的概率是,
故选:C.
9.A
【详解】解:①若两次求助都用在第1题,
根据题意可知,第1题肯定能答对,第2题答对的概率为
故此时该选手通关的概率为:;
②若在第1第2题各用一次求助,
画树状图如下:上层A、B表示第一题剩下的两个选项,下层A、B、C表示第二题剩下的三个选项,
共有6种等可能的结果,其中该选手通关的可能只有1种,故此时该选手通关的概率为:;
③两次求助都用在第2题
画树状图如下:上层A、B、C表示第一题剩下的三个选项,下层A、B表示第二题剩下的二个选项,
共有6种等可能的结果,其中该选手通关的可能只有1种,故此时该选手通关的概率为:.
∵>
∴两次求助都用在第1题,该选手通关的概率大,
故选A.
10.A
【详解】解:图1阴影部分为270°,图2阴影部分为240°,图3每份为45°,阴影部分共4份为180°,图4每份为45°阴影部分共5份为225°,所以①②④③,
故选A.
11.0.9
【详解】解:∵观察表格,发现大量重复试验发芽的频率逐渐稳定在0.9左右,
∴该玉米种子发芽的概率为0.9,
故答案为:0.9.
12.
【详解】∵,
∴阴影部分面积占总面积的,即:顾客转动一次可以打折的概率为.
故答案是:.
13.③
【详解】解:①:频率不是概率,频率会随着重复试验的次数变化而变化,而概率是固定的,故①错误;
②:频率是客观存在的,与试验次数有关,试验次数越多,频率越稳定,故②错误
③:由频率的性质知:随着试验次数的增加,事件发生的频率一般会稳定于概率,故③正确;
④:概率是客观的,在试验前能确定,故④错误.
故答案为:③.
14.10
【详解】解:由题意可得,,
解得,n=10.
经检验,n=10是原方程的根,
故估计n的值为10.
故答案为:10.
15.4
【详解】解:∵产品的抽样合格率为,
∴产品的抽样不合格率为
∴当购买该电子产品足够多时,平均来说,每购4个这样的电子产品,就可能会出现1个次品
故答案为:4.
16.
【详解】解:假设小亮在甲,则小明有甲、乙、丙三种,那么他们要在同一队的可能只有,同理,小亮在乙或丙,他们要在同一队的可能也只有.
17.出海
【详解】解:预测下月好天气的机会是,坏天气的机会是,,
下月是好天气的可能性坏天气的可能性;
又若出海后是好天气,可得收益5000元;若出海后天气变坏,将要损失2000元;若不出海,无论天气好坏都要承担1000元的损失费,
出海的话,获得平均收益(获得收益的数学期望)(元,
不出海:(元,
,
船队队长作出决策为:出海.
故答案为:出海.
18.
【详解】解:在数据,,,,0中,无理数有3个,
∴无理数出现的频率为,
故答案为:.
19.0.5
【详解】解:∵捕捞到鲫鱼的频率稳定在0.25左右,
设鲫鱼的条数为x,可得:
;
解得:x=500,
经检验:x=500是原方程的解且符合实际意义
∴由题意可得,捞到草鱼的概率约为:
,
故答案为:0.5.
20.
【详解】有实数根,
,
∴,
,
又,
对称轴为:,
时,随增大而减小,
,
综上,
可取0,2,
∴,
故答案为:.
21.(1)0.250;(2)见解析;(3)见解析;(4)能,用扑克牌,每一种只取一张,即能替代
【详解】(1)
解:;
;
;
;
;
;
;
;
;
;
(2)
统计图如图
(3)
解:取中数学课本的频率随着取书次数的增加,越来越接近0.25
(4)
能,用扑克牌,每一种只取一张,即能替代.
【点睛】本题主要考查利用频率估算概率的方法,按照步骤解题即可.
22.(1)0.25,理由见解析;(2)②
【详解】(1)
解:摸到白球的概率的估计值是0.25;
理由:大量重复实验下,摸到白球的频率稳定在0.25附近,0.25即概率的估计值;
(2)
解:①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上的概率是;
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲的概率是=0.25;
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数“小于3”的概率是=;
综上所述,符合(1)中结果的试验最有可能的是②,
故答案为:②.
23.(1)0.3,6;(2)6;(3)1
【详解】(1)
解:通过以上实验,摸到红球的概率估计为0.3,
20×0.3=6;
故答案为:0.3,6
(2)
解:因为“摸出黑球”为必然事件,
∴袋子只有黑球,
∴需要拿出所有的红球,即x=6;
故答案为:6
(3)
解:由(1)知红球6个,黑球14个,
拿掉x个红球,加入x个黑球后,则红球(6-x),依题意得:
,
解得x=1,
故红球取出1个.
24.(1);(2)36
【详解】(1)
解:抽查总体数m=50+100+200+300+400+500=1550,
次品件数n=0+4+14+19+24+30=91,
这批衬衣中任抽1件是次品的概率为.
(2)
根据(1)的结论:这批衬衣中任抽1件是次品的概率为0.06,
则600×0.06=36(件).
答:准备36件正品衬衣供顾客调换.
25.(1)0.7;(2)0.4;(3)封闭图形的面积为10π平方米.
【详解】(1)
解:20÷29≈0.69;
59÷91≈0.65;
123÷176≈0.70,
…
当投掷的次数很大时,则m:n的值越来越接近0.7;
故答案为:0.7;
(2)
解:观察表格得:随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在0.4,
故答案为:0.4;
(3)
解:设封闭图形的面积为a,根据题意得:=0.4,
解得:a=10π,
答:封闭图形的面积为10π平方米.
26.(1)0.9;(2)瓶
【详解】解:(1)依题意可知,
今年六月份每月售出(不含降价处理)的酸奶瓶数不高于瓶的概率为;
(2)根据题意可知:
该超市当天售出一瓶酸奶可获利元,降级处理一瓶亏元,
设今年六月销售这种酸奶每天的进货量为瓶,平均每天的利润为元,则:
当时,
,
当时,
,
当时,
,
当时,
,
当时,与时比较,
六月增订的部分,亏本售出的比正常售出的多,
所以其每天的平均利润比时平均每天利润少.
综上所述:时,的值达到最大.
即今年六月份这种酸奶一年的进货量为瓶时,平均每天销售这种酸奶的利润最大.
同课章节目录
