12.2.2三角形全等的判定-SAS 学案
文档属性
| 名称 | 12.2.2三角形全等的判定-SAS 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 09:25:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.2.2三角形全等的判定-SAS 导学案
课题 12.2.2三角形全等的判定-SAS 单元 第12单元 学科 数学 年级 八年级(上)
教材分析 理解三角形全等“边角边”的内容.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.
核心素养分析 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.培养学生观察分析图形能力、动手能力.
学习目标 1.掌握三角形全等的“SAS”条件.2.能运用“SAS”证明简单的三角形全等问题.3.经历探索三角形全等条件的过程,培养学生观察分析图形能力、动手能力.
重点 应用“边角边”证明两个三角形全等,进而得出线段或角相等.
难点 寻找判定三角形全等的条件.
教学过程
课前预学 引入思考 1、判定三角形全等有哪些方法?2、“SSS”的内容是什么?你能用几何语言、文字语言分别表述出来吗?探究1、两边及其夹角能否判定两个三角形全等 已知任意△ABC,画△A'B'C',使A'B'=AB,A'C'=AC,∠A'=∠A.教帅点拨,学生边学边画图,再让学生把画好的△A'B'C',剪下放在△ABC上,观察这两个三角形是否全等●归纳:“边角边”判定方法文字语言:两边和它们的___分别相等的两个三角形____.。(简写成“边角边”或“________ ”).几何语言:在△ABC 和△ DEF中,
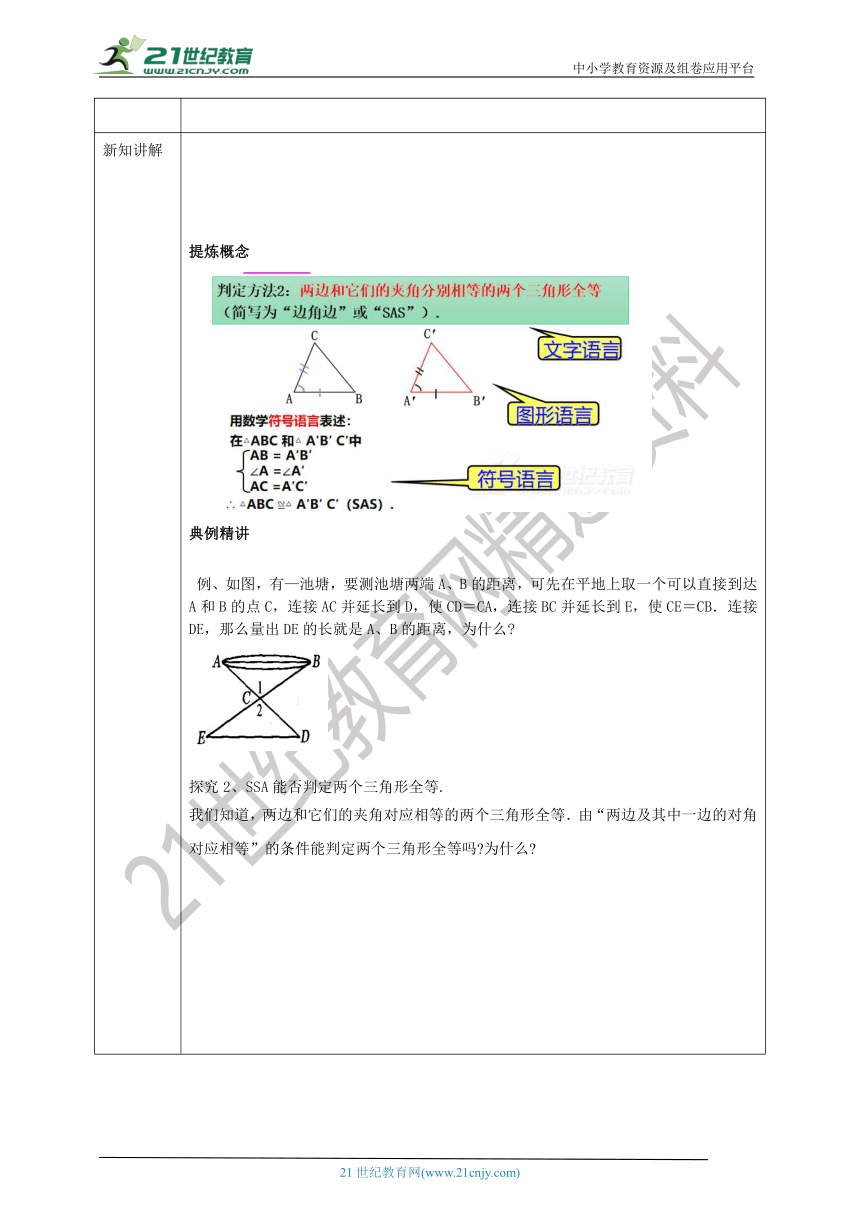
新知讲解 提炼概念典例精讲 例、如图,有—池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么 探究2、SSA能否判定两个三角形全等.我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗 为什么
课堂练习 巩固训练 1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )A.∠A=∠D B.∠E=∠CC.∠A=∠C D.∠ABD=∠EBC 2、如图,AB = AC,若想用“SAS”判定△ABD≌△ACE,则需补充一个条件_________.3.小明做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件标注在图中,小明不用测量就能知道EH=FH吗 为什么 4、已知:如图,AB=AC, BD=CD,E为AD上一点.求证: BE=CE.5.如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系? 答案引入思考 归纳:“边角边”判定方法文字语言:两边和它们的夹角分别相等的两个三角形全等.。(简写成“边角边”或“SAS ”).几何语言:在△ABC 和△ DEF中,∴ △ABC ≌△ DEF(SAS). 提炼概念 典例精讲 例 解:在△ABC和△DEC中,CA=CD , CB=CE .∠ACB=∠DCE(对顶角)△ACB≌△ECD(SAS)∴DE=AB探究2、SSA能否判定两个三角形全等.我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗 为什么 让学生模仿前面的探究方法,画出你认为不合理的图形,归纳得出什么结论?●结论:两边及其中一边的对角对应相等的两个三角形不一定全等.即SSA不能判定全等。巩固训练1.D2.AD = AE3.解:不用测量就能知道EH=FH.理由如下:在△EDH和△FDH中,∴△EDH≌△FDH(SAS),∴EH=FH.4.5.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
12.2.2三角形全等的判定-SAS 导学案
课题 12.2.2三角形全等的判定-SAS 单元 第12单元 学科 数学 年级 八年级(上)
教材分析 理解三角形全等“边角边”的内容.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.
核心素养分析 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.培养学生观察分析图形能力、动手能力.
学习目标 1.掌握三角形全等的“SAS”条件.2.能运用“SAS”证明简单的三角形全等问题.3.经历探索三角形全等条件的过程,培养学生观察分析图形能力、动手能力.
重点 应用“边角边”证明两个三角形全等,进而得出线段或角相等.
难点 寻找判定三角形全等的条件.
教学过程
课前预学 引入思考 1、判定三角形全等有哪些方法?2、“SSS”的内容是什么?你能用几何语言、文字语言分别表述出来吗?探究1、两边及其夹角能否判定两个三角形全等 已知任意△ABC,画△A'B'C',使A'B'=AB,A'C'=AC,∠A'=∠A.教帅点拨,学生边学边画图,再让学生把画好的△A'B'C',剪下放在△ABC上,观察这两个三角形是否全等●归纳:“边角边”判定方法文字语言:两边和它们的___分别相等的两个三角形____.。(简写成“边角边”或“________ ”).几何语言:在△ABC 和△ DEF中,
新知讲解 提炼概念典例精讲 例、如图,有—池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么 探究2、SSA能否判定两个三角形全等.我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗 为什么
课堂练习 巩固训练 1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )A.∠A=∠D B.∠E=∠CC.∠A=∠C D.∠ABD=∠EBC 2、如图,AB = AC,若想用“SAS”判定△ABD≌△ACE,则需补充一个条件_________.3.小明做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件标注在图中,小明不用测量就能知道EH=FH吗 为什么 4、已知:如图,AB=AC, BD=CD,E为AD上一点.求证: BE=CE.5.如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系? 答案引入思考 归纳:“边角边”判定方法文字语言:两边和它们的夹角分别相等的两个三角形全等.。(简写成“边角边”或“SAS ”).几何语言:在△ABC 和△ DEF中,∴ △ABC ≌△ DEF(SAS). 提炼概念 典例精讲 例 解:在△ABC和△DEC中,CA=CD , CB=CE .∠ACB=∠DCE(对顶角)△ACB≌△ECD(SAS)∴DE=AB探究2、SSA能否判定两个三角形全等.我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗 为什么 让学生模仿前面的探究方法,画出你认为不合理的图形,归纳得出什么结论?●结论:两边及其中一边的对角对应相等的两个三角形不一定全等.即SSA不能判定全等。巩固训练1.D2.AD = AE3.解:不用测量就能知道EH=FH.理由如下:在△EDH和△FDH中,∴△EDH≌△FDH(SAS),∴EH=FH.4.5.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
