沪科版八年级数学上册试题 第13章 《三角形中的边角关系、命题与证明》单元测试(含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 第13章 《三角形中的边角关系、命题与证明》单元测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 09:17:28 | ||
图片预览



文档简介
第13章 《三角形中的边角关系、命题与证明》单元测试
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.下面命题中,是假命题的为
A.三角形的中线、角平分线、高都是线段
B.任意三角形的内角和都是
C.三角形的外角大于该三角形任意一个内角
D.直角三角形中的两个锐角互余
2.三边都不相等的三角形有两边长分别为3和5,第三边长是奇数,则其周长为
A.15 B.13 C.11 D.15或13或11
3.给定下列条件,不能判定三角形是直角三角形的是
A. B.
C. D.
4.如图,在三角形中,,,,则
A. B. C. D.
5.一副三角板如图所示摆放,若,则的度数是
A. B. C. D.
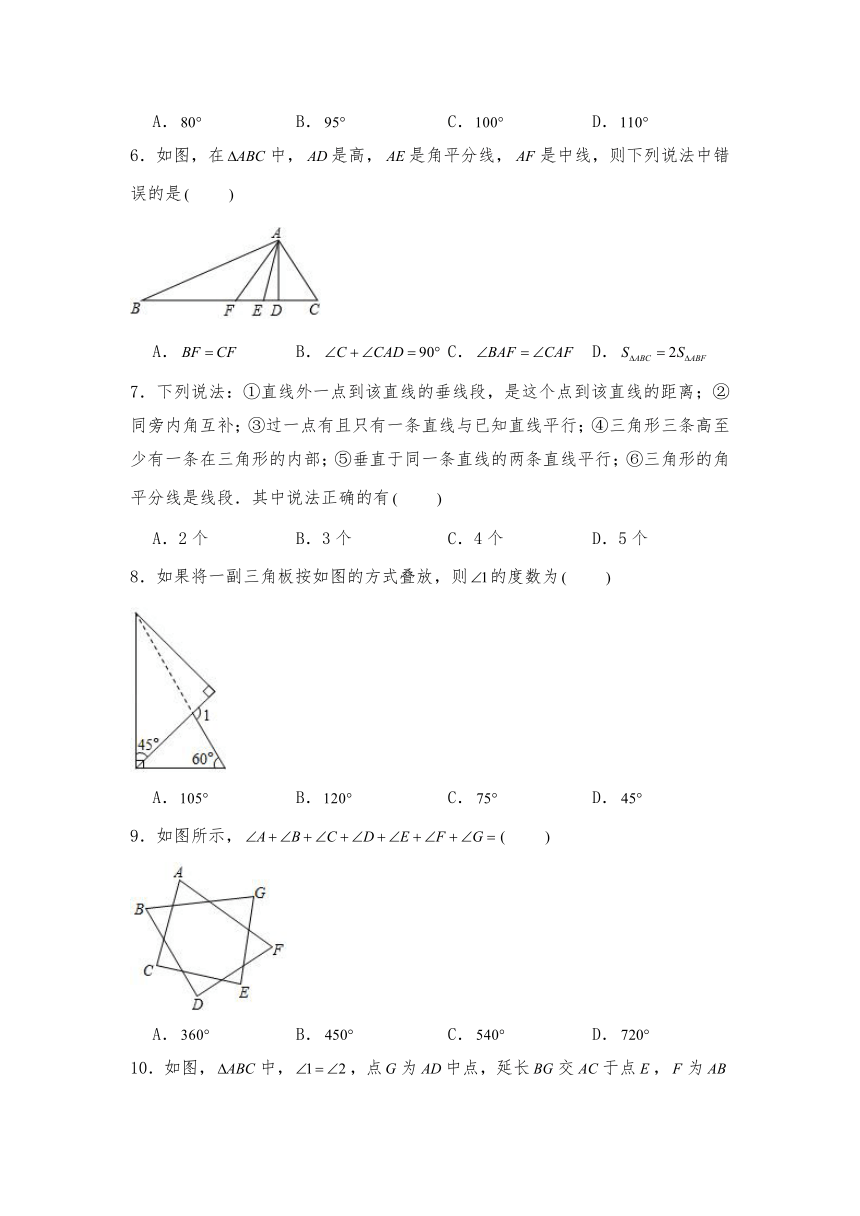
6.如图,在中,是高,是角平分线,是中线,则下列说法中错误的是
A. B. C. D.
7.下列说法:①直线外一点到该直线的垂线段,是这个点到该直线的距离;②同旁内角互补;③过一点有且只有一条直线与已知直线平行;④三角形三条高至少有一条在三角形的内部;⑤垂直于同一条直线的两条直线平行;⑥三角形的角平分线是线段.其中说法正确的有
A.2个 B.3个 C.4个 D.5个
8.如果将一副三角板按如图的方式叠放,则的度数为
A. B. C. D.
9.如图所示,
A. B. C. D.
10.如图,中,,点为中点,延长交于点,为上一点,且于点,下列判断中,①线段是边上的中线;②线段是中边上的高;③与面积相等;④;⑤,其中正确的结论有
A.5个 B.4个 C.3个 D.2个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.的三边长分别为1,3,,且为整数,则的值是 .
12.已知,,是的三边长,化简 .
13.如图中,将边沿虚线翻折,若,则的度数是 度.
14.如图,在中,,三等分,,三等分.若,则 .
15.如图,是的外角的平分线,交的延长线于点,,,则的度数为 .
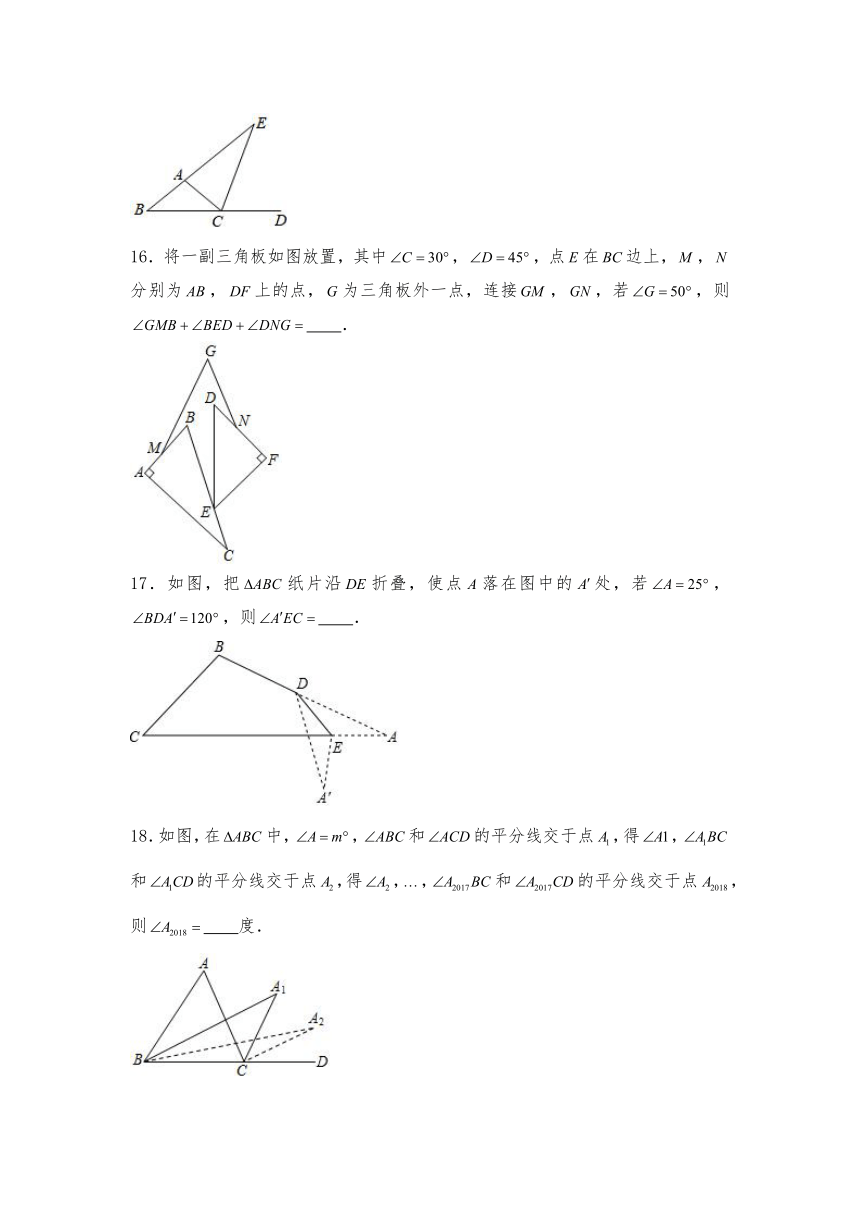
16.将一副三角板如图放置,其中,,点在边上,,分别为,上的点,为三角板外一点,连接,,若,则 .
17.如图,把纸片沿折叠,使点落在图中的处,若,,则 .
18.如图,在中,,和的平分线交于点,得,和的平分线交于点,得,,和的平分线交于点,则 度.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.如图,中,是的平分线,,,求的度数.
20.如图,在三角形中,,,是的中点,点在边上.
(1)若三角形的周长与四边形的周长相等,求线段的长.
(2)若三角形的周长被分成的两部分的差是,求线段的长.
21.如图,在中,,是上一点,平分.
(1)若,,求的度数.
(2)若,,请探求的度数与、度数之间的关系(用含、的代数式表示).
22.如图,已知是中的外角平分线.
(1)若,,求的大小;
(2)请说明.
23.已知:如图,,点、分别在射线、上移动(不与点重合),平分,的反向延长线与的平分线相交于点.
(1)当时、的度数是多少?
(2)随着点、的移动,试问的大小是否变化?请说出你的理由.
24.已知:中,记,.
(1)如图1,若平分,、分别平分的外角和,于点.
①用的代数式表示的度数;
②用的代数式表示的度数;
(2)如图2,若点为的三条内角平分线的交点,且于点.
①请补全图形;
②猜想(1)中的两个结论是否发生变化?如果不变,请说明理由;如果变化,直接写出正确的结论.
25.图1,线段、相交于点,连接、,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,和的平分线和相交于点,并且与、分别相交于、.试解答下列问题:
(1)在图1中,请直接写出、、、之间的数量关系: ;
(2)图2中,当度,度时,求的度数.
(3)图2中和为任意角时,其他条件不变,试问与、之间存在着怎样的数量关系.
如图,点、分别在射线、上运动(不与点重合).
(1)如图1,若,、的平分线交于点,则 ;
(2)如图2,若,、的平分线交于点,则 ;
(3)如图2,若,的外角、的平分线交于点,求与之间的数量关系,并求出的度数;
(4)如图3,若,是的平分线,的反向延长线与的平分线交于点.试问:随着点、的运动,的大小会变吗?如果不会,求的度数;如果会,请说明理由.
答案
一、选择题
..........
二、填空题
11.3.
12..
13.55.
14.;
15..
16..
17..
18..
三、解答题
19.解:是的平分线,
,
,,
设,则,,
,
解得,
,,
.
20.解:(1)由图可知三角形的周长,四边形的周长,
又三角形的周长与四边形的周长相等,为中点,
,,
即,
,,
,
.
(2)由三角形的周长被分成的两部分的差是2,可得方程
①或②.
解①得,解②得.
故长为或.
21.解:(1),,
,
,
,
,
是的平分线,
,
;
(2),,
,
,
,
,
是的角平分线,
,
.
22.解:(1),,
;
(2)是中的外角平分线,
,
是的外角,
,
,
是的外角,
,
.
23.解:(1),,
.
平分,
.
平分,
.
又,
.
(2)的大小不变,理由如下:
,平分,
.
平分,
.
又,
,
的大小不发生变化.
24.解:(1)①如图、分别平分的外角和
;
②在中,,
;
(2)①如图2所示,
②中的两个结论发生了变化,
,
,
点为的三条内角平分线的交点,
,,
,
;
,
,
,
.
25.解:(1)由题知,,
,
故答案为:;
(2)由(1)可得,,①
同理可得,,
和的平分线是和,
,②
由②①得,,
即,
,
故;
(3)由(2)可知.
26.解:(1),
,
、的平分线交于点,
,
,
故答案为:135;
(2)在中,
,
、的平分线交于点,
,
即,
;
故答案为:;
(3)、分别是和的角平分线,
,,,,
即,
同理:,
四边形内角和等于,
,
由(1)知:,
,
,
;
(4)的度数不变,;
理由如下:
,
,
、分别是和的角平分线,
,,
,
(等量代换),
,
,
.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.下面命题中,是假命题的为
A.三角形的中线、角平分线、高都是线段
B.任意三角形的内角和都是
C.三角形的外角大于该三角形任意一个内角
D.直角三角形中的两个锐角互余
2.三边都不相等的三角形有两边长分别为3和5,第三边长是奇数,则其周长为
A.15 B.13 C.11 D.15或13或11
3.给定下列条件,不能判定三角形是直角三角形的是
A. B.
C. D.
4.如图,在三角形中,,,,则
A. B. C. D.
5.一副三角板如图所示摆放,若,则的度数是
A. B. C. D.
6.如图,在中,是高,是角平分线,是中线,则下列说法中错误的是
A. B. C. D.
7.下列说法:①直线外一点到该直线的垂线段,是这个点到该直线的距离;②同旁内角互补;③过一点有且只有一条直线与已知直线平行;④三角形三条高至少有一条在三角形的内部;⑤垂直于同一条直线的两条直线平行;⑥三角形的角平分线是线段.其中说法正确的有
A.2个 B.3个 C.4个 D.5个
8.如果将一副三角板按如图的方式叠放,则的度数为
A. B. C. D.
9.如图所示,
A. B. C. D.
10.如图,中,,点为中点,延长交于点,为上一点,且于点,下列判断中,①线段是边上的中线;②线段是中边上的高;③与面积相等;④;⑤,其中正确的结论有
A.5个 B.4个 C.3个 D.2个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.的三边长分别为1,3,,且为整数,则的值是 .
12.已知,,是的三边长,化简 .
13.如图中,将边沿虚线翻折,若,则的度数是 度.
14.如图,在中,,三等分,,三等分.若,则 .
15.如图,是的外角的平分线,交的延长线于点,,,则的度数为 .
16.将一副三角板如图放置,其中,,点在边上,,分别为,上的点,为三角板外一点,连接,,若,则 .
17.如图,把纸片沿折叠,使点落在图中的处,若,,则 .
18.如图,在中,,和的平分线交于点,得,和的平分线交于点,得,,和的平分线交于点,则 度.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.如图,中,是的平分线,,,求的度数.
20.如图,在三角形中,,,是的中点,点在边上.
(1)若三角形的周长与四边形的周长相等,求线段的长.
(2)若三角形的周长被分成的两部分的差是,求线段的长.
21.如图,在中,,是上一点,平分.
(1)若,,求的度数.
(2)若,,请探求的度数与、度数之间的关系(用含、的代数式表示).
22.如图,已知是中的外角平分线.
(1)若,,求的大小;
(2)请说明.
23.已知:如图,,点、分别在射线、上移动(不与点重合),平分,的反向延长线与的平分线相交于点.
(1)当时、的度数是多少?
(2)随着点、的移动,试问的大小是否变化?请说出你的理由.
24.已知:中,记,.
(1)如图1,若平分,、分别平分的外角和,于点.
①用的代数式表示的度数;
②用的代数式表示的度数;
(2)如图2,若点为的三条内角平分线的交点,且于点.
①请补全图形;
②猜想(1)中的两个结论是否发生变化?如果不变,请说明理由;如果变化,直接写出正确的结论.
25.图1,线段、相交于点,连接、,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,和的平分线和相交于点,并且与、分别相交于、.试解答下列问题:
(1)在图1中,请直接写出、、、之间的数量关系: ;
(2)图2中,当度,度时,求的度数.
(3)图2中和为任意角时,其他条件不变,试问与、之间存在着怎样的数量关系.
如图,点、分别在射线、上运动(不与点重合).
(1)如图1,若,、的平分线交于点,则 ;
(2)如图2,若,、的平分线交于点,则 ;
(3)如图2,若,的外角、的平分线交于点,求与之间的数量关系,并求出的度数;
(4)如图3,若,是的平分线,的反向延长线与的平分线交于点.试问:随着点、的运动,的大小会变吗?如果不会,求的度数;如果会,请说明理由.
答案
一、选择题
..........
二、填空题
11.3.
12..
13.55.
14.;
15..
16..
17..
18..
三、解答题
19.解:是的平分线,
,
,,
设,则,,
,
解得,
,,
.
20.解:(1)由图可知三角形的周长,四边形的周长,
又三角形的周长与四边形的周长相等,为中点,
,,
即,
,,
,
.
(2)由三角形的周长被分成的两部分的差是2,可得方程
①或②.
解①得,解②得.
故长为或.
21.解:(1),,
,
,
,
,
是的平分线,
,
;
(2),,
,
,
,
,
是的角平分线,
,
.
22.解:(1),,
;
(2)是中的外角平分线,
,
是的外角,
,
,
是的外角,
,
.
23.解:(1),,
.
平分,
.
平分,
.
又,
.
(2)的大小不变,理由如下:
,平分,
.
平分,
.
又,
,
的大小不发生变化.
24.解:(1)①如图、分别平分的外角和
;
②在中,,
;
(2)①如图2所示,
②中的两个结论发生了变化,
,
,
点为的三条内角平分线的交点,
,,
,
;
,
,
,
.
25.解:(1)由题知,,
,
故答案为:;
(2)由(1)可得,,①
同理可得,,
和的平分线是和,
,②
由②①得,,
即,
,
故;
(3)由(2)可知.
26.解:(1),
,
、的平分线交于点,
,
,
故答案为:135;
(2)在中,
,
、的平分线交于点,
,
即,
;
故答案为:;
(3)、分别是和的角平分线,
,,,,
即,
同理:,
四边形内角和等于,
,
由(1)知:,
,
,
;
(4)的度数不变,;
理由如下:
,
,
、分别是和的角平分线,
,,
,
(等量代换),
,
,
.
