沪科版八年级数学上册试题 一课一练14.2三角形全等的判定(含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 一课一练14.2三角形全等的判定(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 138.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 09:19:16 | ||
图片预览


文档简介
14.2三角形全等的判定
一、选择题
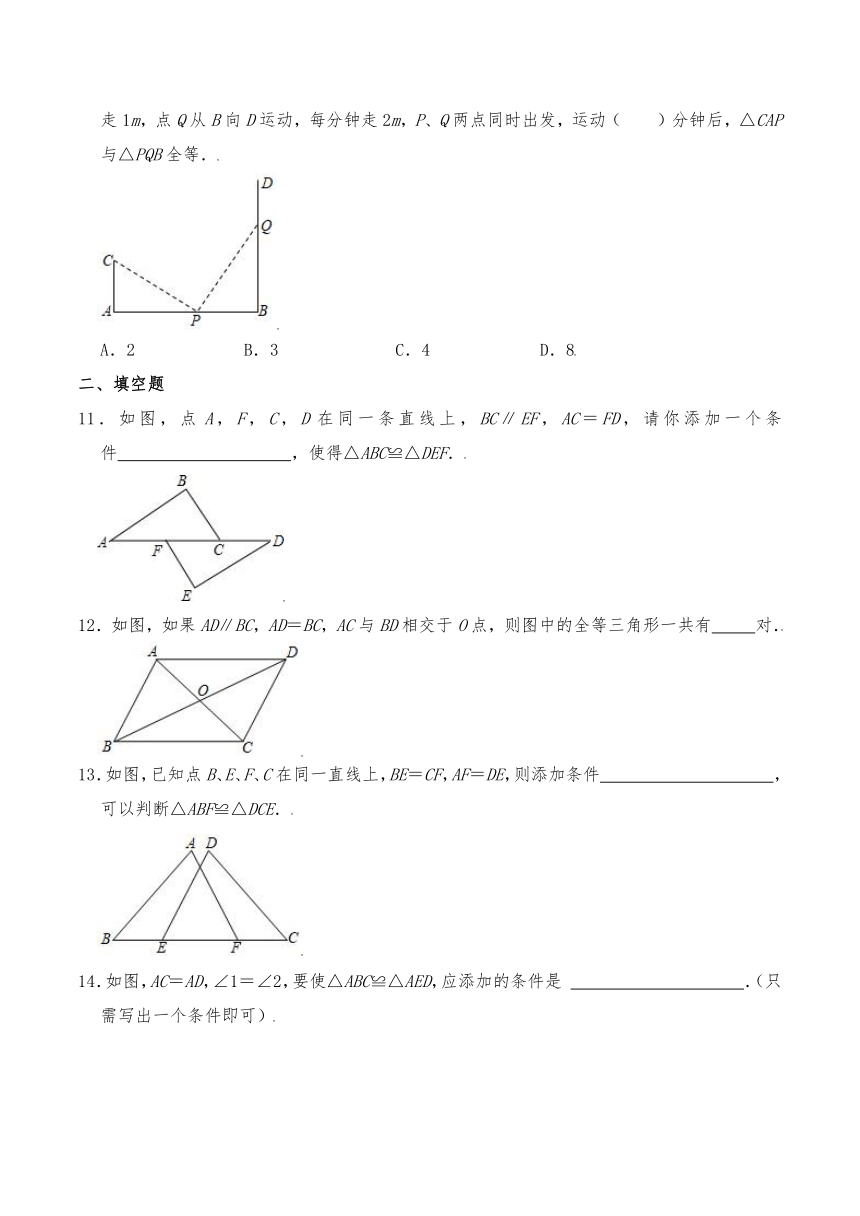
1.如图,已知∠ABC=∠DCB,添加下列条件不能说明△ABC≌△DCB的是( )
A.AC=DB B.∠A=∠D C.AB=DC D.∠ACB=∠DBC
2.根据下列图中所给定的条件,找出全等的三角形( )
A.①和② B.②和③ C.①和③ D.①和④
3.根据下列已知条件,能唯一画出△ABC的是( )
A.AB=3,BC=4,CA=8 B.∠C=90°,AB=6
C.AB=4,BC=3,∠A=30° D.∠A=60°,∠B=45°,AB=4
4.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB B.BC C.DC D.AE+AC
5.如图,E,F是BD上的两点,BE=DF,∠AEF=∠CFE,添加下列一个条件后,仍无法判定△AED≌△CFB的是( )
A.∠B=∠D B.AE=CF C.AD=BC D.AD∥BC
6.如图所示,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.BD=CD B.∠B=∠C C.AB=AC D.AD平分∠BAC
7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=DC,∠A=∠D B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD D.BC=EC,∠B=∠E
8.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E B.AC=DF C.∠ACD=∠BFE D.BF=CD
9.若按给定的三个条件画一个三角形,图形唯一,则所给条件不可能是( )
A.两边一夹角 B.两角一夹边 C.三边 D.三角
10.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A.2 B.3 C.4 D.8
二、填空题
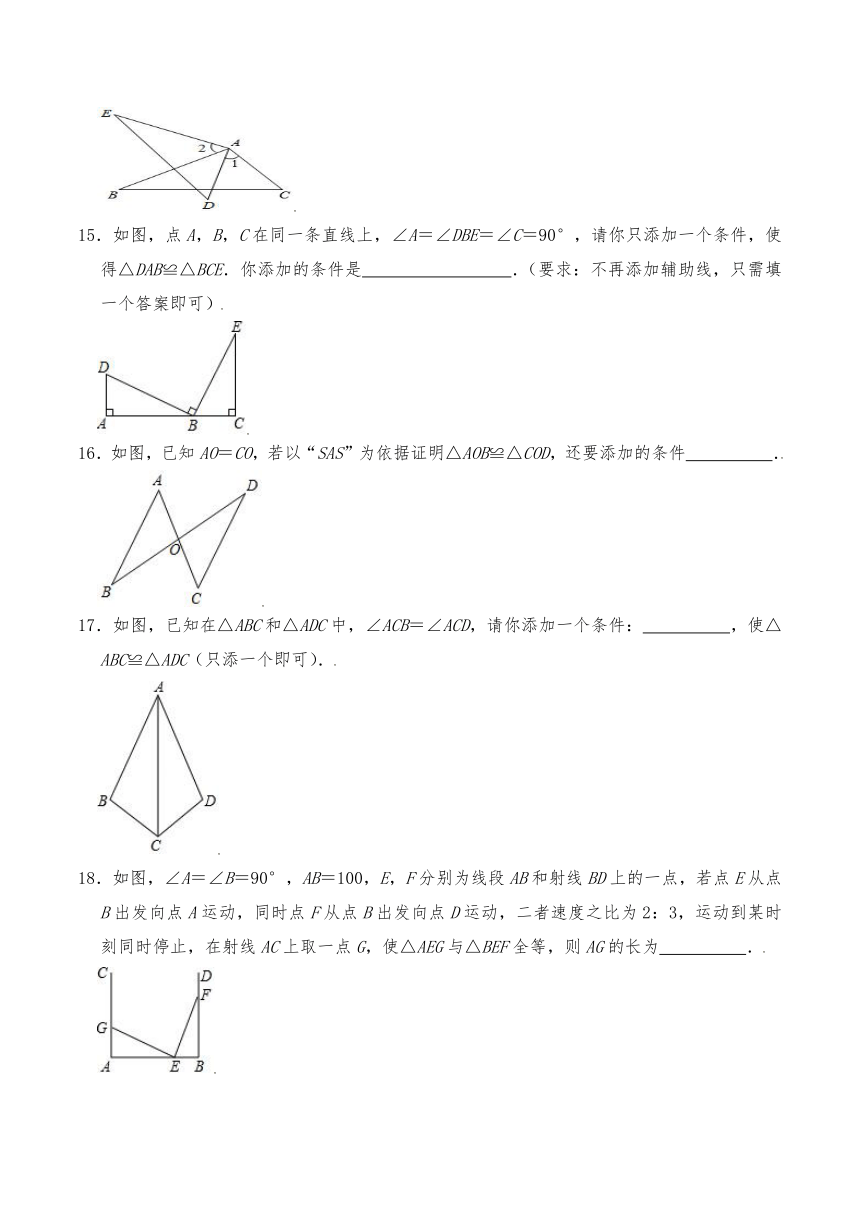
11.如图,点A,F,C,D在同一条直线上,BC∥EF,AC=FD,请你添加一个条件 ,使得△ABC≌△DEF.
12.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,则图中的全等三角形一共有 对.
13.如图,已知点B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件 ,可以判断△ABF≌△DCE.
14.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 .(只需写出一个条件即可)
15.如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件,使得△DAB≌△BCE.你添加的条件是 .(要求:不再添加辅助线,只需填一个答案即可)
16.如图,已知AO=CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的条件 .
17.如图,已知在△ABC和△ADC中,∠ACB=∠ACD,请你添加一个条件: ,使△ABC≌△ADC(只添一个即可).
18.如图,∠A=∠B=90°,AB=100,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为2:3,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
三、解答题
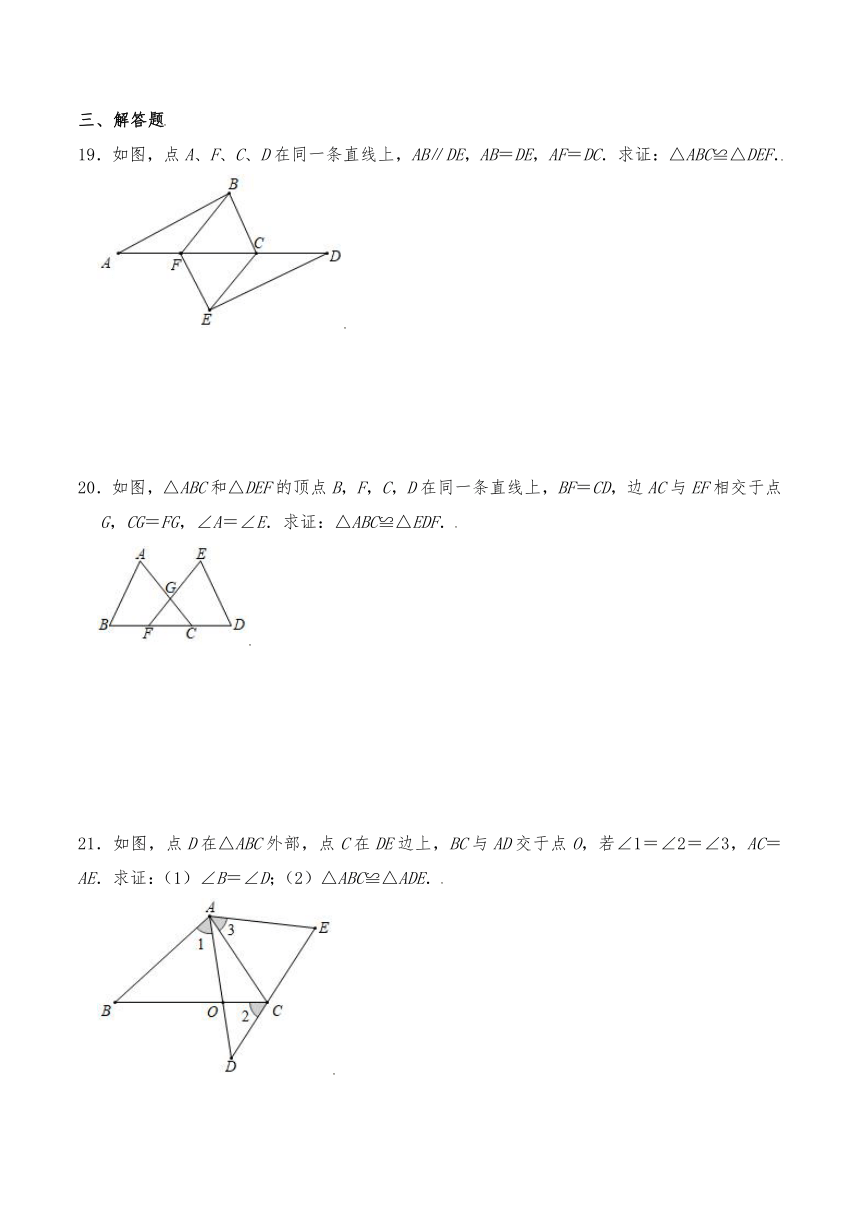
19.如图,点A、F、C、D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:△ABC≌△DEF.
20.如图,△ABC和△DEF的顶点B,F,C,D在同一条直线上,BF=CD,边AC与EF相交于点G,CG=FG,∠A=∠E.求证:△ABC≌△EDF.
21.如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.求证:(1)∠B=∠D;(2)△ABC≌△ADE.
22.如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
23.如图,已知等腰三角形ABC,两腰AB,AC的垂直平分线DF,EG,分别交BC,CB的延长线于点F,G.连接AG,AF.
(1)猜想∠AGB和∠AFC的大小关系,并证明.
(2)求证:△AGB≌△AFC.
24.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
答案
一、选择题
A.D.D.A.C.C.A.D.D.C.
二、填空题
11.BC=EF或∠B=∠E或∠A=∠D(答案不唯一).
12.4.
13.∠AFB=∠DEC或AB=DC.
14.∠B=∠E或∠C=∠D或AB=AE.
15.DB=BE(答案不唯一).
16.BO=DO.
17.BC=DC.
18.40或75.
三、解答题
19.证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
20.证明:∵FG=CG,
∴∠ACB=∠DFE,
∵BF=CD,FC=FC,
∴BF+FC=CD+FC,
即BC=DF,
在△ABC与△EDF中
,
∴△ABC≌△EDF(AAS).
21.证明:(1)∵∠1=∠3,
∴∠1+∠DAC=∠3+∠DAC,
即∠BAC=∠DAE,
∵∠E=∠180°﹣∠3﹣∠ACE,∠ACB=180°﹣∠2﹣∠ACE,
∵∠2=∠3,∠ACE=∠ACE,
∴∠ACB=∠E,
在△ABC与△ADE中
,
∴△ABC≌△ADE(ASA),
∴∠B=∠D.
(2)由(1)可得△ABC≌△ADE.
22.解:(1)AD∥BE,
理由:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
23.(1)猜想∠AGB=∠AFC.
证明:∵GE是AC的垂直平分线,
∴GA=GC,
∴△GAC是等腰三角形,
∴EG是∠AGB的平分线,
∴∠AGE=∠CGE,
在Rt△GEC中,∠CGE=90°﹣∠ACB,
∴∠AGB=2∠CGE=2(90°﹣∠ACB),
同理可证:∠AFC=2∠BFD=2(90°﹣∠ABC),
又∵△ABC是等腰三角形,
∴∠ACB=∠ABC,
∴∠AGB=∠AFC;
(2)证明:∵△ABC是等腰三角形,
∴∠ABC=∠ACB,
∵∠ABC+∠ABG=180°,∠ACB+∠ACF=180°,
∴∠ABG=∠ACF(等角的补角相等),
在△AGB和△AFC中,
,
∴△AGB≌△AFC(AAS).
24.解:(1)△ACP≌△BPQ,
∵AC⊥AB,BD⊥AB
∴∠A=∠B=90°
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
在△ACP和△BPQ中,,
∴△ACP≌△BPQ;
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t
解得:x,t.
一、选择题
1.如图,已知∠ABC=∠DCB,添加下列条件不能说明△ABC≌△DCB的是( )
A.AC=DB B.∠A=∠D C.AB=DC D.∠ACB=∠DBC
2.根据下列图中所给定的条件,找出全等的三角形( )
A.①和② B.②和③ C.①和③ D.①和④
3.根据下列已知条件,能唯一画出△ABC的是( )
A.AB=3,BC=4,CA=8 B.∠C=90°,AB=6
C.AB=4,BC=3,∠A=30° D.∠A=60°,∠B=45°,AB=4
4.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB B.BC C.DC D.AE+AC
5.如图,E,F是BD上的两点,BE=DF,∠AEF=∠CFE,添加下列一个条件后,仍无法判定△AED≌△CFB的是( )
A.∠B=∠D B.AE=CF C.AD=BC D.AD∥BC
6.如图所示,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.BD=CD B.∠B=∠C C.AB=AC D.AD平分∠BAC
7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=DC,∠A=∠D B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD D.BC=EC,∠B=∠E
8.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E B.AC=DF C.∠ACD=∠BFE D.BF=CD
9.若按给定的三个条件画一个三角形,图形唯一,则所给条件不可能是( )
A.两边一夹角 B.两角一夹边 C.三边 D.三角
10.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A.2 B.3 C.4 D.8
二、填空题
11.如图,点A,F,C,D在同一条直线上,BC∥EF,AC=FD,请你添加一个条件 ,使得△ABC≌△DEF.
12.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,则图中的全等三角形一共有 对.
13.如图,已知点B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件 ,可以判断△ABF≌△DCE.
14.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是 .(只需写出一个条件即可)
15.如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件,使得△DAB≌△BCE.你添加的条件是 .(要求:不再添加辅助线,只需填一个答案即可)
16.如图,已知AO=CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的条件 .
17.如图,已知在△ABC和△ADC中,∠ACB=∠ACD,请你添加一个条件: ,使△ABC≌△ADC(只添一个即可).
18.如图,∠A=∠B=90°,AB=100,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为2:3,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
三、解答题
19.如图,点A、F、C、D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:△ABC≌△DEF.
20.如图,△ABC和△DEF的顶点B,F,C,D在同一条直线上,BF=CD,边AC与EF相交于点G,CG=FG,∠A=∠E.求证:△ABC≌△EDF.
21.如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.求证:(1)∠B=∠D;(2)△ABC≌△ADE.
22.如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
23.如图,已知等腰三角形ABC,两腰AB,AC的垂直平分线DF,EG,分别交BC,CB的延长线于点F,G.连接AG,AF.
(1)猜想∠AGB和∠AFC的大小关系,并证明.
(2)求证:△AGB≌△AFC.
24.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
答案
一、选择题
A.D.D.A.C.C.A.D.D.C.
二、填空题
11.BC=EF或∠B=∠E或∠A=∠D(答案不唯一).
12.4.
13.∠AFB=∠DEC或AB=DC.
14.∠B=∠E或∠C=∠D或AB=AE.
15.DB=BE(答案不唯一).
16.BO=DO.
17.BC=DC.
18.40或75.
三、解答题
19.证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
20.证明:∵FG=CG,
∴∠ACB=∠DFE,
∵BF=CD,FC=FC,
∴BF+FC=CD+FC,
即BC=DF,
在△ABC与△EDF中
,
∴△ABC≌△EDF(AAS).
21.证明:(1)∵∠1=∠3,
∴∠1+∠DAC=∠3+∠DAC,
即∠BAC=∠DAE,
∵∠E=∠180°﹣∠3﹣∠ACE,∠ACB=180°﹣∠2﹣∠ACE,
∵∠2=∠3,∠ACE=∠ACE,
∴∠ACB=∠E,
在△ABC与△ADE中
,
∴△ABC≌△ADE(ASA),
∴∠B=∠D.
(2)由(1)可得△ABC≌△ADE.
22.解:(1)AD∥BE,
理由:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
23.(1)猜想∠AGB=∠AFC.
证明:∵GE是AC的垂直平分线,
∴GA=GC,
∴△GAC是等腰三角形,
∴EG是∠AGB的平分线,
∴∠AGE=∠CGE,
在Rt△GEC中,∠CGE=90°﹣∠ACB,
∴∠AGB=2∠CGE=2(90°﹣∠ACB),
同理可证:∠AFC=2∠BFD=2(90°﹣∠ABC),
又∵△ABC是等腰三角形,
∴∠ACB=∠ABC,
∴∠AGB=∠AFC;
(2)证明:∵△ABC是等腰三角形,
∴∠ABC=∠ACB,
∵∠ABC+∠ABG=180°,∠ACB+∠ACF=180°,
∴∠ABG=∠ACF(等角的补角相等),
在△AGB和△AFC中,
,
∴△AGB≌△AFC(AAS).
24.解:(1)△ACP≌△BPQ,
∵AC⊥AB,BD⊥AB
∴∠A=∠B=90°
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
在△ACP和△BPQ中,,
∴△ACP≌△BPQ;
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t
解得:x,t.
