八年级数学上册试题 一课一练14.2三角形全等的判定--直角三角形全等的判定-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 一课一练14.2三角形全等的判定--直角三角形全等的判定-沪科版(含答案) | 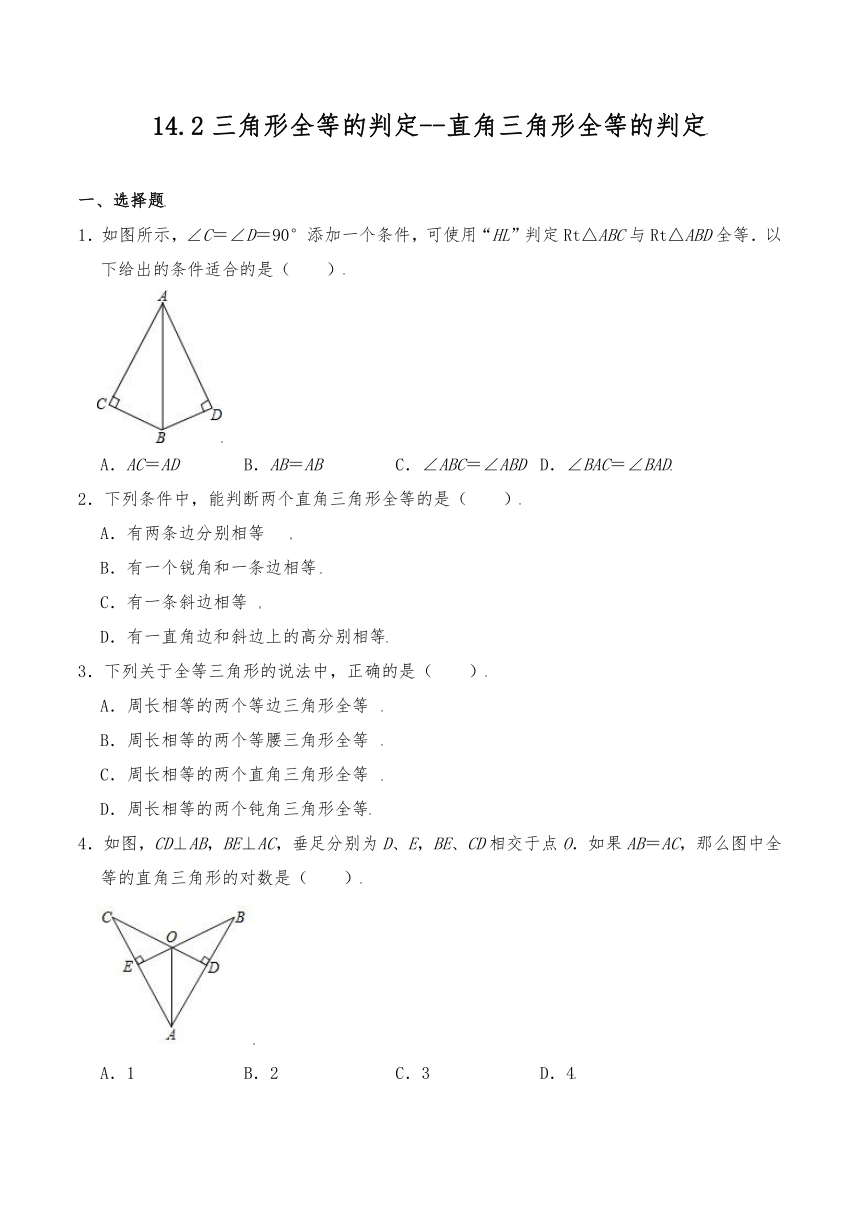 | |
| 格式 | zip | ||
| 文件大小 | 120.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 09:21:35 | ||
图片预览



文档简介
14.2三角形全等的判定--直角三角形全等的判定
一、选择题
1.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD
2.下列条件中,能判断两个直角三角形全等的是( )
A.有两条边分别相等
B.有一个锐角和一条边相等
C.有一条斜边相等
D.有一直角边和斜边上的高分别相等
3.下列关于全等三角形的说法中,正确的是( )
A.周长相等的两个等边三角形全等
B.周长相等的两个等腰三角形全等
C.周长相等的两个直角三角形全等
D.周长相等的两个钝角三角形全等
4.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )
A.1 B.2 C.3 D.4
5.下列语句中不正确的是( )
A.斜边和一锐角对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两个锐角相等的两个直角三角形全等
D.有一直角边和一锐角对应相等的两个直角三角形全等
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.75°
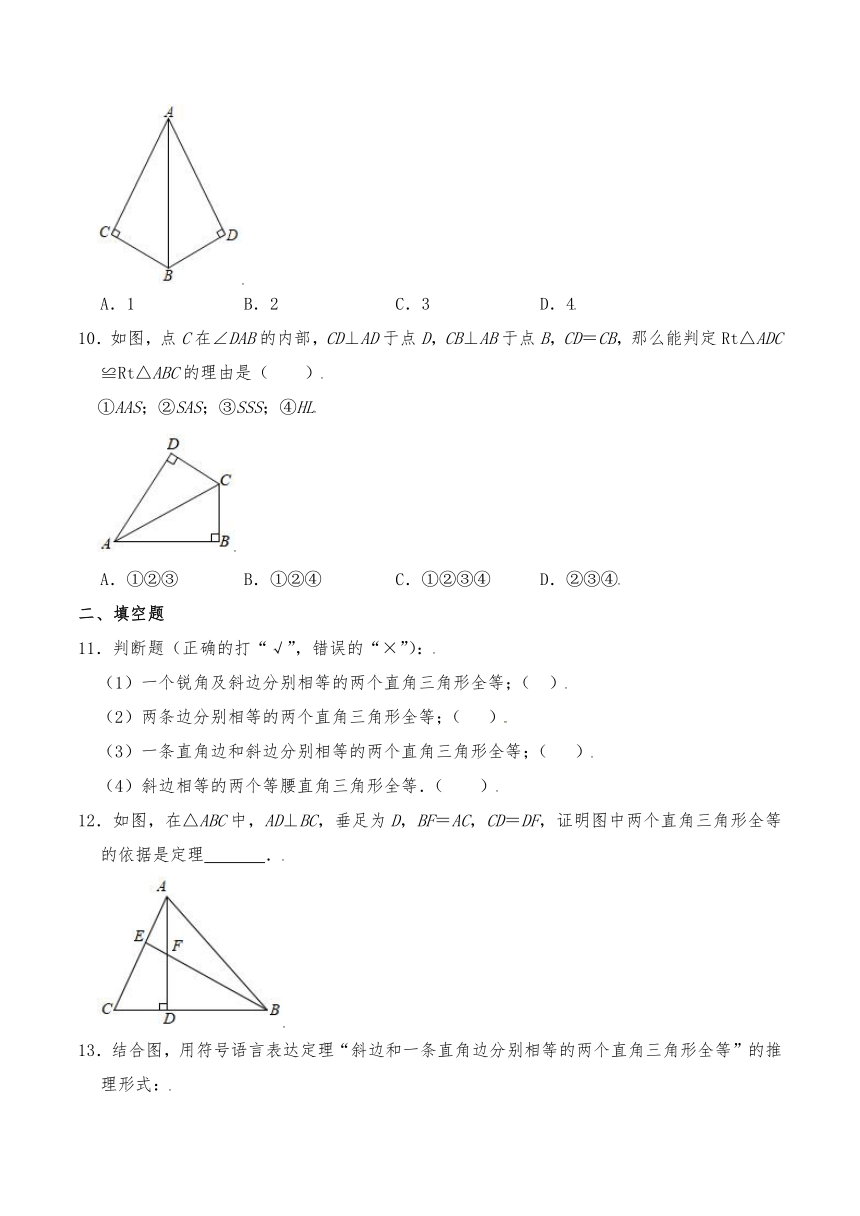
7.如图,点C在∠DAB的内部,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么Rt△ADC≌Rt△ABC的理由是( )
A.SAS B.ASA C.HL D.SSS
8.下列条件中不能判定两个直角三角形全等的是( )
A.两个锐角分别对应相等
B.两条直角边分别对应相等
C.一条直角边和斜边分别对应相等
D.一个锐角和一条斜边分别对应相等
9.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
10.如图,点C在∠DAB的内部,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么能判定Rt△ADC≌Rt△ABC的理由是( )
①AAS;②SAS;③SSS;④HL
A.①②③ B.①②④ C.①②③④ D.②③④
二、填空题
11.判断题(正确的打“√”,错误的“×”):
(1)一个锐角及斜边分别相等的两个直角三角形全等;( )
(2)两条边分别相等的两个直角三角形全等;( )
(3)一条直角边和斜边分别相等的两个直角三角形全等;( )
(4)斜边相等的两个等腰直角三角形全等.( )
12.如图,在△ABC中,AD⊥BC,垂足为D,BF=AC,CD=DF,证明图中两个直角三角形全等的依据是定理 .
13.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
14.如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是 .
15.如图,Rt△ABC和Rt△EDF中,AB∥DF,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.
16.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是 .(不添加字母和辅助线)
17.下列说法正确的有 个.
(1)两条边对应相等的两个直角三角形全等.
(2)有一锐角和斜边对应相等的两直角三角形全等.
(3)一条直角边和一个锐角对应相等的两直角三角形全等.
(4)面积相等的两个直角三角形全等.
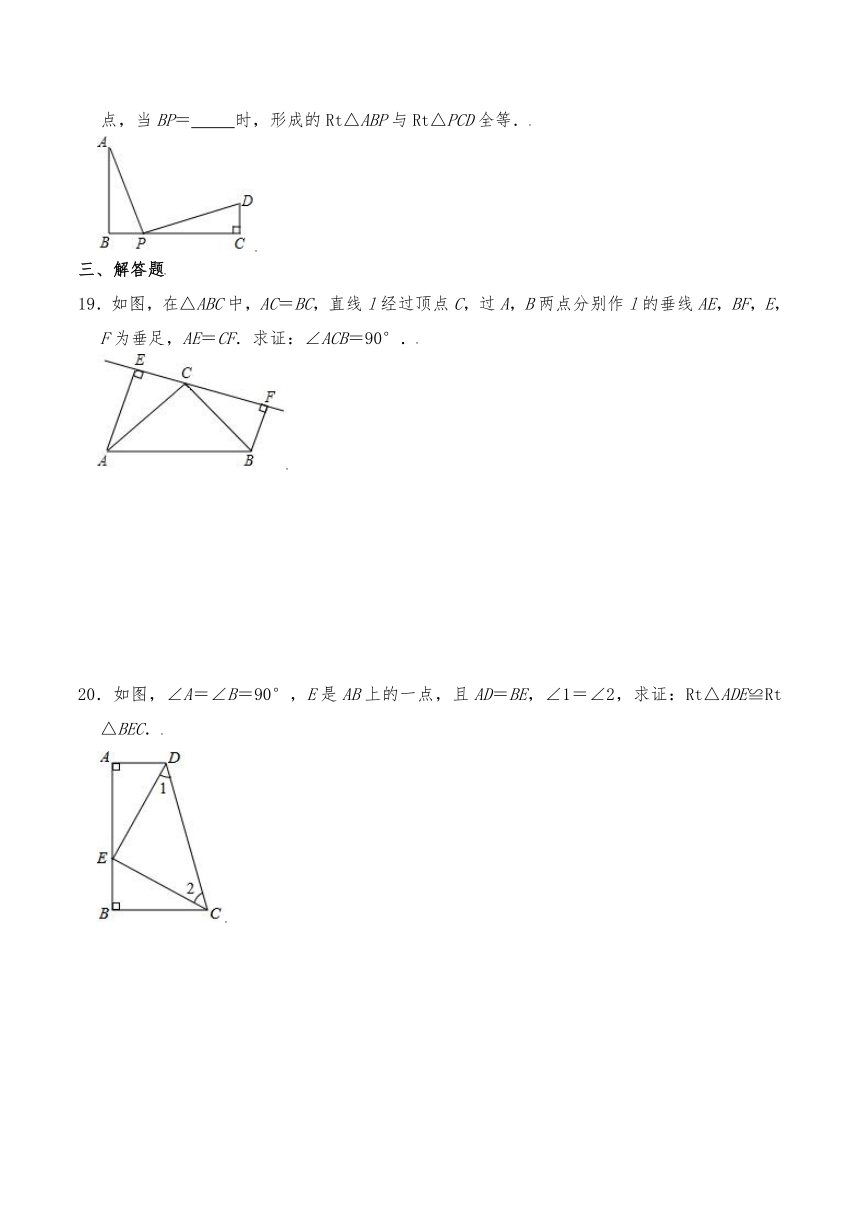
18.如图,AB⊥BC、DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,当BP= 时,形成的Rt△ABP与Rt△PCD全等.
三、解答题
19.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
20.如图,∠A=∠B=90°,E是AB上的一点,且AD=BE,∠1=∠2,求证:Rt△ADE≌Rt△BEC.
21.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
22.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
23.如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
24.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
答案
一、选择题
A.D.A.C.C.B.C.A.D.C.
二、填空题
11.(1)√;(2)×;(3)√;(4)√.
12.HL.
13.AB=DE.
14.AC=BD(或者AD=BC).
15.AB=DF(答案不唯一).
16.AB=DC(答案不唯一)
17.3.
18.2.
三、解答题
19.证明:如图,在Rt△ACE和Rt△CBF中,
∴Rt△ACE≌Rt△CBF(HL),
∴∠EAC=∠BCF,
∵∠EAC+∠ACE=90°,
∴∠ACE+∠BCF=90°,
∴∠ACB=180°﹣90°=90°.
20.证明:∵∠1=∠2,
∴DE=CE.
∵∠A=∠B=90°,
∴△ADE和△EBC是直角三角形,而AD=BE.
∴Rt△ADE≌Rt△BEC(HL)
21.证明:(1)在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
22.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
23.根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=10;
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合,不合题意.
综上所述,当点P运动到线段AC中点时,△ABC与△QPA全等.
24.(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
一、选择题
1.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD
2.下列条件中,能判断两个直角三角形全等的是( )
A.有两条边分别相等
B.有一个锐角和一条边相等
C.有一条斜边相等
D.有一直角边和斜边上的高分别相等
3.下列关于全等三角形的说法中,正确的是( )
A.周长相等的两个等边三角形全等
B.周长相等的两个等腰三角形全等
C.周长相等的两个直角三角形全等
D.周长相等的两个钝角三角形全等
4.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )
A.1 B.2 C.3 D.4
5.下列语句中不正确的是( )
A.斜边和一锐角对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两个锐角相等的两个直角三角形全等
D.有一直角边和一锐角对应相等的两个直角三角形全等
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.75°
7.如图,点C在∠DAB的内部,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么Rt△ADC≌Rt△ABC的理由是( )
A.SAS B.ASA C.HL D.SSS
8.下列条件中不能判定两个直角三角形全等的是( )
A.两个锐角分别对应相等
B.两条直角边分别对应相等
C.一条直角边和斜边分别对应相等
D.一个锐角和一条斜边分别对应相等
9.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
10.如图,点C在∠DAB的内部,CD⊥AD于点D,CB⊥AB于点B,CD=CB,那么能判定Rt△ADC≌Rt△ABC的理由是( )
①AAS;②SAS;③SSS;④HL
A.①②③ B.①②④ C.①②③④ D.②③④
二、填空题
11.判断题(正确的打“√”,错误的“×”):
(1)一个锐角及斜边分别相等的两个直角三角形全等;( )
(2)两条边分别相等的两个直角三角形全等;( )
(3)一条直角边和斜边分别相等的两个直角三角形全等;( )
(4)斜边相等的两个等腰直角三角形全等.( )
12.如图,在△ABC中,AD⊥BC,垂足为D,BF=AC,CD=DF,证明图中两个直角三角形全等的依据是定理 .
13.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
14.如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是 .
15.如图,Rt△ABC和Rt△EDF中,AB∥DF,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.
16.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是 .(不添加字母和辅助线)
17.下列说法正确的有 个.
(1)两条边对应相等的两个直角三角形全等.
(2)有一锐角和斜边对应相等的两直角三角形全等.
(3)一条直角边和一个锐角对应相等的两直角三角形全等.
(4)面积相等的两个直角三角形全等.
18.如图,AB⊥BC、DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,当BP= 时,形成的Rt△ABP与Rt△PCD全等.
三、解答题
19.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
20.如图,∠A=∠B=90°,E是AB上的一点,且AD=BE,∠1=∠2,求证:Rt△ADE≌Rt△BEC.
21.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
22.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
23.如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
24.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
答案
一、选择题
A.D.A.C.C.B.C.A.D.C.
二、填空题
11.(1)√;(2)×;(3)√;(4)√.
12.HL.
13.AB=DE.
14.AC=BD(或者AD=BC).
15.AB=DF(答案不唯一).
16.AB=DC(答案不唯一)
17.3.
18.2.
三、解答题
19.证明:如图,在Rt△ACE和Rt△CBF中,
∴Rt△ACE≌Rt△CBF(HL),
∴∠EAC=∠BCF,
∵∠EAC+∠ACE=90°,
∴∠ACE+∠BCF=90°,
∴∠ACB=180°﹣90°=90°.
20.证明:∵∠1=∠2,
∴DE=CE.
∵∠A=∠B=90°,
∴△ADE和△EBC是直角三角形,而AD=BE.
∴Rt△ADE≌Rt△BEC(HL)
21.证明:(1)在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
22.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
23.根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=10;
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合,不合题意.
综上所述,当点P运动到线段AC中点时,△ABC与△QPA全等.
24.(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
