沪科版八年级数学上册11.2 图形在坐标系中的平移 课件 (共19张PPT)
文档属性
| 名称 | 沪科版八年级数学上册11.2 图形在坐标系中的平移 课件 (共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 11:03:45 | ||
图片预览




文档简介
(共19张PPT)
第十一章 平面直角坐标系
11.2 图形在坐标系中的平移
导入新课
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
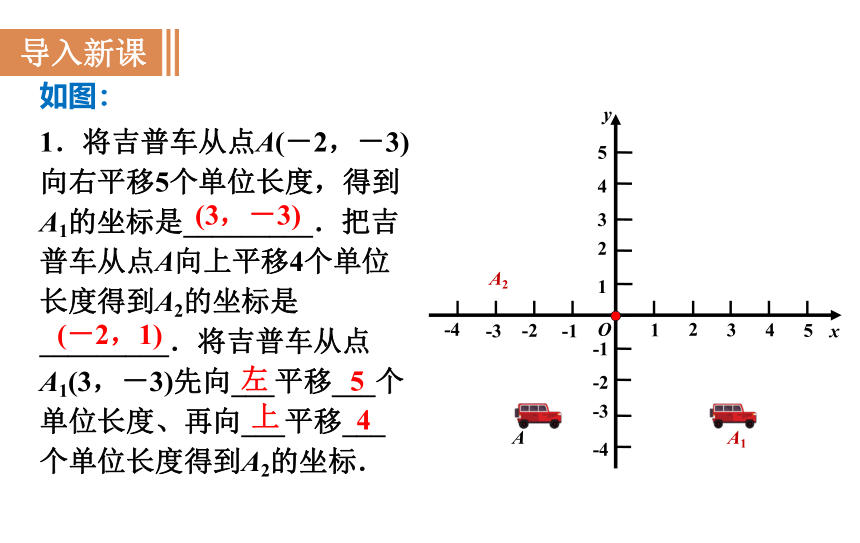
1.将吉普车从点A(-2,-3)向右平移5个单位长度,得到A1的坐标是_________.把吉普车从点A向上平移4个单位长度得到A2的坐标是_________.将吉普车从点A1(3,-3)先向___平移___个单位长度、再向___平移___个单位长度得到A2的坐标.
如图:
A
A2
A1
(3,-3)
(-2,1)
左
5
上
4
2.你认为点(-2,-3)在向上、向下平移及向左、向右平移的变化规律是什么?
答:向上、下平移纵坐标加上、减去一个数,向左、右平移横坐标减去、加上一个数.
探究新知
平面直角坐标系中点的平移
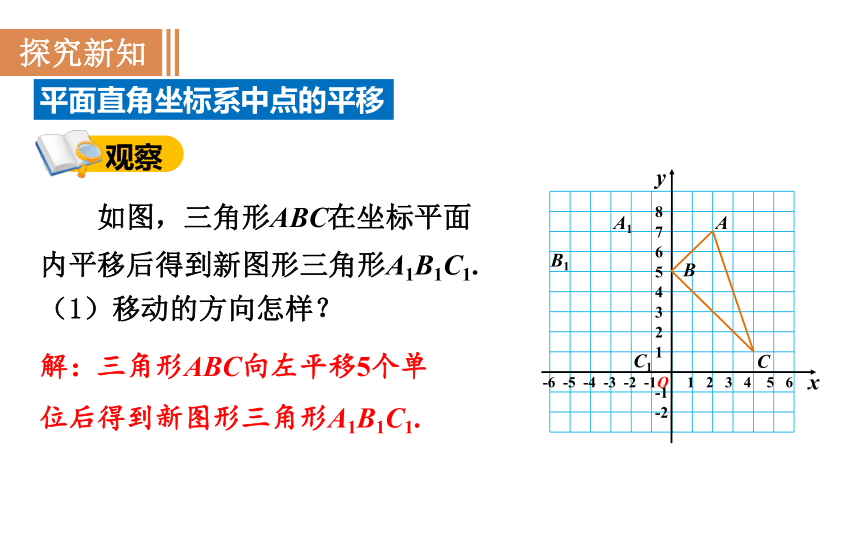
如图,三角形ABC在坐标平面内平移后得到新图形三角形A1B1C1.
y
8
7
6
5
4
3
2
1
-1
-2
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
O
A
B
C
A1
B1
C1
观察
(1)移动的方向怎样?
解:三角形ABC向左平移5个单位后得到新图形三角形A1B1C1.
y
8
7
6
5
4
3
2
1
-1
-2
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
O
A
B
C
A1
B1
C1
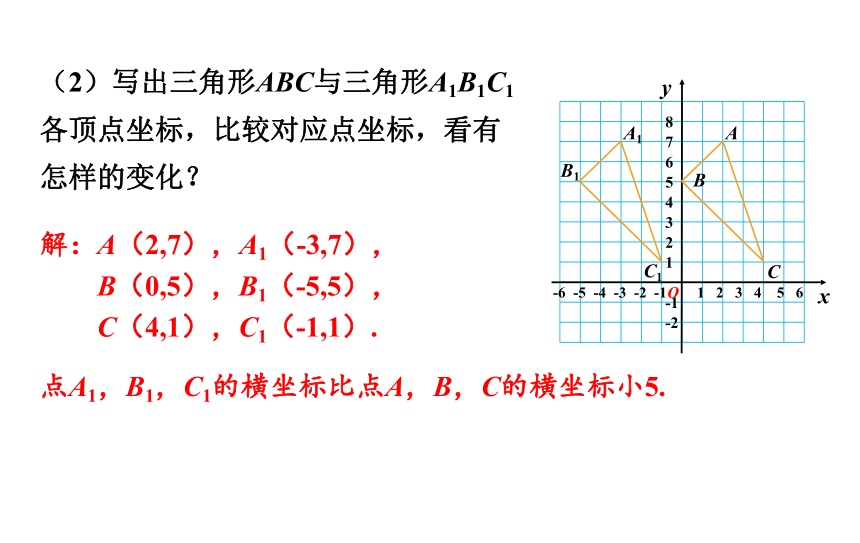
(2)写出三角形ABC与三角形A1B1C1各顶点坐标,比较对应点坐标,看有怎样的变化?
解:A(2,7),A1(-3,7),
B(0,5),B1(-5,5),
C(4,1),C1(-1,1).
点A1,B1,C1的横坐标比点A,B,C的横坐标小5.
y
8
7
6
5
4
3
2
1
-1
-2
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
O
A
B
C
A2
B2
C2
(3)如果三角形ABC向下平移2个单位,得到三角形A2B2C2.写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化?
解:A(2,7),A2(2,5),
B(0,5),B2(0,3),
C(4,1),C2(4,-1).
点A2,B2,C2的纵坐标比点A,B,C的纵坐标小2.
知识归纳
平面直角坐标系中点的平移规律
向右平移a个单位对应点 P1(x+a,y)
特殊形式
图形上的点P(x,y)
向上平移b个单位对应点P3(x,y+b)
向左平移a个单位对应点P2(x-a,y)
向下平移b个单位对应点P4(x,y-b)
范例
在平面直角坐标系中,点P(2,3)先向左平移3个单位,再向下平移4个单位,得到点的坐标为 ( )
A.(5,7) B.(-1,-1)
C.(-1,1) D.(5,-1)
B
例题与练习
仿例
若将点P(1,-m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点(m,n)的坐标为( )
A.(3,-2) B.(2,-3)
C.(3,2) D.(-2,3)
分析:根据平移中点的变化规律:横坐标右移加,纵坐标上移加,可得Q点的坐标,从而列出有关m和n的方程,即可求出m、n的值.
D
变例
若将点P先向左平移3个长度单位,再向下平移2个长度单位后的对应点为Q(-1,3),则P点的坐标为( )
A.(-1,3) B.(-4,1)
C.(2,5) D.(1,0)
解析:求点P的坐标即把点Q向右平移3个长度单位,再向上平移2个长度单位,则对应点P的横坐标为-1+3=2,纵坐标为3+2=5.∴点P的坐标为(2,5). 故选C.
C
例题与练习
例 如图,将三角形ABC先向右平移6个单位,再向下平移2个单位得到三角形A1B1C1.
写出各顶点变动前后的坐标.
y
8
7
6
5
4
3
2
1
-1
-2
x
-4 -3 -2 -1 1 2 3 4 5 6 7
O
A
B
C
A1
B1
C1
解:用→代表平移,有
A(-2,6)→(4,6)→A1(4,4)
B(-4,4)→(2,4)→B1(2,2)
C(1,1)→(7,1)→C1(7,-1)
平面直角坐标系中图形的平移
仿例
解:(1)点A向左平移1个单位长度,再向上平移2个单位长度,得到点B;
说出下列由点A到点B是怎样平移的?
(1)A(x,y)―→B(x-1,y+2);
(2)A(x,y)―→B(x+3,y-2);
(3)A(x+3,y-2)―→B(x,y).
(2)点A向右平移3个单位长度,再向下平移2个单位长度,得到点B;
(3)点A向左平移3个单位长度,再向上平移2个单位长度,得到点B.
1.平面直角坐标系中图形的平移与其上面点的平移是否相同?
思考
答:相同.
在平面直角坐标系内,一个图形怎样移动,那么这个图形上的各个点就怎么移动.
思考
2.把平面直角坐标系中的一个图形,按下面的要求平移,那么,图形上任一个点的坐标(x,y)是如何变化的?
(1)向左或向右移动a(a>0)个单位;
(x,y)→(x+a,y)
(x,y)→(x-a,y)
向右
向左
(2)向上或向下移动b(b>0)个单位;
(x,y)→(x,y+b)
(x,y)→(x,y-b)
向上
向下
(3)向左或向右移动a(a>0)个单位;再向上或向下移动b(b>0)个单位.
(x,y)→(x+a,y+b)
(x,y)→(x+a,y-b)
向右向上
向右向下
(x,y)→(x-a,y+b)
(x,y)→(x-a,y-b)
向左向上
向左向下
随堂练习
1.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标 为______.
2.将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
3.将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
(3,4)
(3,-1)
(-1,2)
5.将点A(3,2)向上平移2个单位长度,向左平移4个单位长度得到A1,则A1的坐标为 .
(-1,4)
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
向右平移8个单位长度
右平移2个单位长度
6.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A(﹣1,1) B(﹣1,﹣2) C(﹣1,2) D(1,2)
A
7.下面每个图中的图②是由图①平移得到的,描述各图是如何移动的,并写出图①、图②各顶点的坐标.
x
-4 -2 2 4 6
y
4
2
-2
-4
O
①
②
(x,y)→(x+5,y-6)
(-4,2)
(-3,4)
(2,2)
(1,-4)
(2,-2)
(7,-4)
x
1 2 3 4 5
y
3
2
1
-1
-2
-3
①
②
(5,2)
(5,3)
(1,2)
(1,3)
(5,-3)
(5,-2)
(1,-2)
(1,-3)
O
(x,y)→(x,y-5)
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标加上一个正数,向右平移
横坐标减去一个正数,向左平移
横坐标不变
纵坐标加上一个正数,向上平移
纵坐标减去一个正数,向下平移
第十一章 平面直角坐标系
11.2 图形在坐标系中的平移
导入新课
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
1.将吉普车从点A(-2,-3)向右平移5个单位长度,得到A1的坐标是_________.把吉普车从点A向上平移4个单位长度得到A2的坐标是_________.将吉普车从点A1(3,-3)先向___平移___个单位长度、再向___平移___个单位长度得到A2的坐标.
如图:
A
A2
A1
(3,-3)
(-2,1)
左
5
上
4
2.你认为点(-2,-3)在向上、向下平移及向左、向右平移的变化规律是什么?
答:向上、下平移纵坐标加上、减去一个数,向左、右平移横坐标减去、加上一个数.
探究新知
平面直角坐标系中点的平移
如图,三角形ABC在坐标平面内平移后得到新图形三角形A1B1C1.
y
8
7
6
5
4
3
2
1
-1
-2
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
O
A
B
C
A1
B1
C1
观察
(1)移动的方向怎样?
解:三角形ABC向左平移5个单位后得到新图形三角形A1B1C1.
y
8
7
6
5
4
3
2
1
-1
-2
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
O
A
B
C
A1
B1
C1
(2)写出三角形ABC与三角形A1B1C1各顶点坐标,比较对应点坐标,看有怎样的变化?
解:A(2,7),A1(-3,7),
B(0,5),B1(-5,5),
C(4,1),C1(-1,1).
点A1,B1,C1的横坐标比点A,B,C的横坐标小5.
y
8
7
6
5
4
3
2
1
-1
-2
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
O
A
B
C
A2
B2
C2
(3)如果三角形ABC向下平移2个单位,得到三角形A2B2C2.写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化?
解:A(2,7),A2(2,5),
B(0,5),B2(0,3),
C(4,1),C2(4,-1).
点A2,B2,C2的纵坐标比点A,B,C的纵坐标小2.
知识归纳
平面直角坐标系中点的平移规律
向右平移a个单位对应点 P1(x+a,y)
特殊形式
图形上的点P(x,y)
向上平移b个单位对应点P3(x,y+b)
向左平移a个单位对应点P2(x-a,y)
向下平移b个单位对应点P4(x,y-b)
范例
在平面直角坐标系中,点P(2,3)先向左平移3个单位,再向下平移4个单位,得到点的坐标为 ( )
A.(5,7) B.(-1,-1)
C.(-1,1) D.(5,-1)
B
例题与练习
仿例
若将点P(1,-m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点(m,n)的坐标为( )
A.(3,-2) B.(2,-3)
C.(3,2) D.(-2,3)
分析:根据平移中点的变化规律:横坐标右移加,纵坐标上移加,可得Q点的坐标,从而列出有关m和n的方程,即可求出m、n的值.
D
变例
若将点P先向左平移3个长度单位,再向下平移2个长度单位后的对应点为Q(-1,3),则P点的坐标为( )
A.(-1,3) B.(-4,1)
C.(2,5) D.(1,0)
解析:求点P的坐标即把点Q向右平移3个长度单位,再向上平移2个长度单位,则对应点P的横坐标为-1+3=2,纵坐标为3+2=5.∴点P的坐标为(2,5). 故选C.
C
例题与练习
例 如图,将三角形ABC先向右平移6个单位,再向下平移2个单位得到三角形A1B1C1.
写出各顶点变动前后的坐标.
y
8
7
6
5
4
3
2
1
-1
-2
x
-4 -3 -2 -1 1 2 3 4 5 6 7
O
A
B
C
A1
B1
C1
解:用→代表平移,有
A(-2,6)→(4,6)→A1(4,4)
B(-4,4)→(2,4)→B1(2,2)
C(1,1)→(7,1)→C1(7,-1)
平面直角坐标系中图形的平移
仿例
解:(1)点A向左平移1个单位长度,再向上平移2个单位长度,得到点B;
说出下列由点A到点B是怎样平移的?
(1)A(x,y)―→B(x-1,y+2);
(2)A(x,y)―→B(x+3,y-2);
(3)A(x+3,y-2)―→B(x,y).
(2)点A向右平移3个单位长度,再向下平移2个单位长度,得到点B;
(3)点A向左平移3个单位长度,再向上平移2个单位长度,得到点B.
1.平面直角坐标系中图形的平移与其上面点的平移是否相同?
思考
答:相同.
在平面直角坐标系内,一个图形怎样移动,那么这个图形上的各个点就怎么移动.
思考
2.把平面直角坐标系中的一个图形,按下面的要求平移,那么,图形上任一个点的坐标(x,y)是如何变化的?
(1)向左或向右移动a(a>0)个单位;
(x,y)→(x+a,y)
(x,y)→(x-a,y)
向右
向左
(2)向上或向下移动b(b>0)个单位;
(x,y)→(x,y+b)
(x,y)→(x,y-b)
向上
向下
(3)向左或向右移动a(a>0)个单位;再向上或向下移动b(b>0)个单位.
(x,y)→(x+a,y+b)
(x,y)→(x+a,y-b)
向右向上
向右向下
(x,y)→(x-a,y+b)
(x,y)→(x-a,y-b)
向左向上
向左向下
随堂练习
1.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标 为______.
2.将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
3.将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
(3,4)
(3,-1)
(-1,2)
5.将点A(3,2)向上平移2个单位长度,向左平移4个单位长度得到A1,则A1的坐标为 .
(-1,4)
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
向右平移8个单位长度
右平移2个单位长度
6.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A(﹣1,1) B(﹣1,﹣2) C(﹣1,2) D(1,2)
A
7.下面每个图中的图②是由图①平移得到的,描述各图是如何移动的,并写出图①、图②各顶点的坐标.
x
-4 -2 2 4 6
y
4
2
-2
-4
O
①
②
(x,y)→(x+5,y-6)
(-4,2)
(-3,4)
(2,2)
(1,-4)
(2,-2)
(7,-4)
x
1 2 3 4 5
y
3
2
1
-1
-2
-3
①
②
(5,2)
(5,3)
(1,2)
(1,3)
(5,-3)
(5,-2)
(1,-2)
(1,-3)
O
(x,y)→(x,y-5)
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标加上一个正数,向右平移
横坐标减去一个正数,向左平移
横坐标不变
纵坐标加上一个正数,向上平移
纵坐标减去一个正数,向下平移
