沪科版八年级数学上册12.1.2 函数的表示方法-列表法与解析法 课件 (共22张PPT)
文档属性
| 名称 | 沪科版八年级数学上册12.1.2 函数的表示方法-列表法与解析法 课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 542.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 11:09:41 | ||
图片预览








文档简介
(共22张PPT)
第十二章 一次函数
12.1 函数
第2课时 函数的表示方法—列表法与解析法
旧知回顾
导入新课
1.什么是常量?什么是变量?什么是函数?
2.如何判断两个变量间的函数关系?
答:在某一变化过程中,数值保持不变的量叫常量.
数值发生变化的量叫变量.
一般地,设在某一变化过程中有两个变量x,y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值和它对应,那么就说x是自变量,y是x的函数.
答:遵循定义中,对于自变量的每一个确定的值,因变量都有唯一确定值与其对应,则因变量是自变量的函数.
探究新知
求自变量取值范围
上节课我们研究了三个问题,它们都反映了两个变量间的函数关系,回头看一下:
问题1 用热气球探测高空气象
时间t/min
海拔高度h/m
0
1800
1
1830
2
1860
3
1890
4
1920
5
1950
6
1980
7
2010
… …
… …
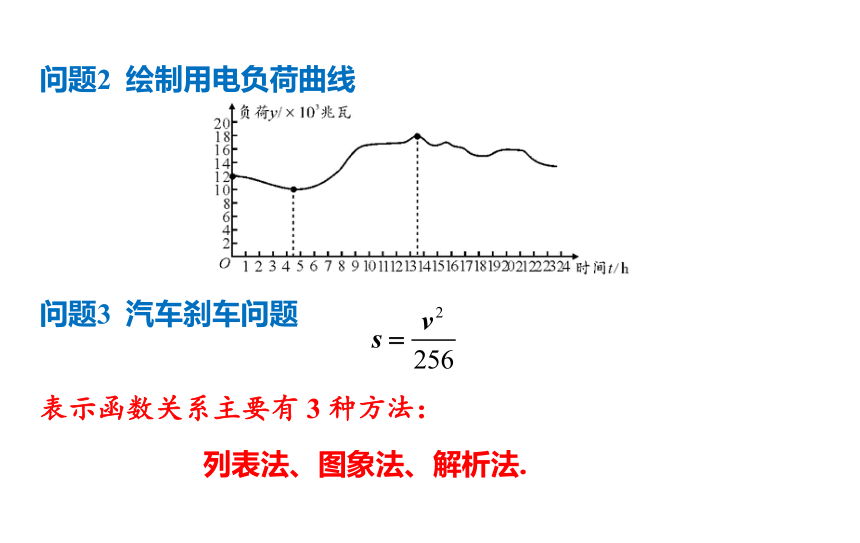
问题2 绘制用电负荷曲线
问题3 汽车刹车问题
表示函数关系主要有 3 种方法:
列表法、图象法、解析法.
知识归纳
列表法
解析法
图象法
定义
实例
优点
通过列出自变量的值,与对应函数值的表格来表示函数关系的方法
问题1
具体反映了函数随自变量的数值对应关系
用数学式子表示函数关系的方法
问题3
准确地反映了函数随自变量的数量关系
用图象来表示两个变量间的函数关系的方法
问题2
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法的区别
例题与练习
分析:在(1)(2)中,x 取任何实数,函数都有意义;在(3)中,x=2时,函数无意义;在(4)中,x<3时,函数无意义.
例1
求下列函数中自变量x的取值范围:
(1)y=2x+4; (2)y=-2x2;
(3) (4)
解 : (1)x为全体实数.
(2)x为全体实数.
(3)x≠2.
(4)x≥3.
(1)解析式是整式时,自变量取全体实数;
知识归纳
(2)解析式是分式时,自变量的取值应使分母不为0;
(3)解析式是平方根时,自变量取值范围应使被开方数大于 或等于0;
(4)解决实际问题时,必须既符合理论又满足实际,特别注意:不要先化简关系式再求取值范围.
当 x = 3 时,求下列函数的函数值:
解: (1)当x=3时,y=2x+4=2×3+4=10.
(2)当x=3时,y=-2x2=-2×32=-18.
(3)当x=3时,
(4)当x=3时,
例2
(1)y=2x+4; (2)y=-2x2;
(3) (4)
例题与练习
范例
求下列函数中自变量x的取值范围:
解:(1)任意实数;
(2)任意实数;
(3)x≠-2;
(4)x≥2.
解析:根据题意得x-1≥0且 x-2≠0,
解得x≥1且 x ≠2.
故答案为x≥1且 x ≠2.
x≥1且x≠2
仿例
函数y = 有意义,则自变量x的取值范围是
__________________.
1.求下列函数中自变量x的取值范围:
解:(1)x为全体实数.
(2)x≠4.
(3)x≥5.
(4)x为全体实数.
练习
解:(1)当x=9时,y=-2;当x=10时,
(2)当x=9时, ;当x=10时,
2.求下列函数当x=9和x=10的函数值:
一个游泳池内有水 300 m3,现打开排水管以每时 25 m3 排出量排水.
(1)写出游泳池内剩余水量Q (m3)与排水时间t(h)之间的函数表达式;
(2)写出自变量 t 的取值范围;
在实际问题中求自变量取值范围
例3
解:(1)排水后的剩水量Q是排水时间t的函数,有
Q=-25t+300;
(2)由于池中共有300m3水,每时排25m3,全部排完只需300÷25=12(h),故自变量t的取值范围是0≤t≤12.
(3)开始排水5 h 后,游泳池中还有多少水?
(4)当游泳池中还剩 150 m3 水时,已经排水多少时间?
解:(3)当t=5,代入上式得Q=-5×25+300=175(m3),
即排水5h后,池中还有水175m3.
(4)当Q=150时,由150=-25t+300,得t=6,即已经排水6h.
范例
水箱内原有水200升,7点30分打开水龙头,以2升/分的速度放水,设经t分钟时,水箱内存水y升.
(1)求y关于t的函数关系式和自变量的取值范围;
(2)7∶55时,水箱内还有多少水?
(3)几点几分水箱内的水恰好放完?
解:(1)y=200-2t,
(2)即t=25,y=200-2×25,
(3)当y=0,即200-2t=0,t=100,
∵水100分钟放完,
∴自变量取值范围为0≤t≤100;
7∶55时,水箱还有150升水;
7∶30+1时40分=9点10分,故9点10分水箱水恰好放完.
仿例
如图,在靠墙(墙长为18m)的地方围建一个长方形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m.
(1)试写出养鸡场平行于墙的长y(m)与垂直于墙的长x(m)的函数关系式;
(2)求自变量x的取值范围.
解:(1)y=35-2x;
(2)∵y=35-2x≤18,
∴x≥8.5,
∵35-2x>0,x<17.5,
∴自变量x取值范围是8.5≤x<17.5.
在实际问题中确定自变量的取值范围,主
要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
知识归纳
实际问题中自变量的取值范围
求函数值
范例1:
函数y= ,当x=1时,y= ;当x=3时,y= .
3
-3
范例2:
已知函数y= ,当x=-4时,y= .
0
例题与练习
范例3:
如图,根据流程图中的程序,当输出数值y=5时,输入数值x是( )
C
随堂练习
1.一列火车以80km/h的速度匀速行驶.
(1)写出它行驶的路程 s km与时间 t h之间的函数表达式;
(2)当t=10时,s是多少?
解:(1)s=80t;
(2)当t=10时,s=800.
2.求下列函数中自变量x的取值范围:
x ≠0
x ≠-1
x≥0
x为一切实数
x≥2
x为一切实数
3.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) 10 20 30
y(单位:万元/台) 60 55 50
则y与x之间的解析式是( )
A.y=80- 2x B.y=40+ 2x
D.y=60-
C
C. y=65-
课堂小结
函数的表示方法
列表法、解析法和图象法
自变量的取值范围
使含自变量的等式有意义
使实际问题有意义
第十二章 一次函数
12.1 函数
第2课时 函数的表示方法—列表法与解析法
旧知回顾
导入新课
1.什么是常量?什么是变量?什么是函数?
2.如何判断两个变量间的函数关系?
答:在某一变化过程中,数值保持不变的量叫常量.
数值发生变化的量叫变量.
一般地,设在某一变化过程中有两个变量x,y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值和它对应,那么就说x是自变量,y是x的函数.
答:遵循定义中,对于自变量的每一个确定的值,因变量都有唯一确定值与其对应,则因变量是自变量的函数.
探究新知
求自变量取值范围
上节课我们研究了三个问题,它们都反映了两个变量间的函数关系,回头看一下:
问题1 用热气球探测高空气象
时间t/min
海拔高度h/m
0
1800
1
1830
2
1860
3
1890
4
1920
5
1950
6
1980
7
2010
… …
… …
问题2 绘制用电负荷曲线
问题3 汽车刹车问题
表示函数关系主要有 3 种方法:
列表法、图象法、解析法.
知识归纳
列表法
解析法
图象法
定义
实例
优点
通过列出自变量的值,与对应函数值的表格来表示函数关系的方法
问题1
具体反映了函数随自变量的数值对应关系
用数学式子表示函数关系的方法
问题3
准确地反映了函数随自变量的数量关系
用图象来表示两个变量间的函数关系的方法
问题2
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法的区别
例题与练习
分析:在(1)(2)中,x 取任何实数,函数都有意义;在(3)中,x=2时,函数无意义;在(4)中,x<3时,函数无意义.
例1
求下列函数中自变量x的取值范围:
(1)y=2x+4; (2)y=-2x2;
(3) (4)
解 : (1)x为全体实数.
(2)x为全体实数.
(3)x≠2.
(4)x≥3.
(1)解析式是整式时,自变量取全体实数;
知识归纳
(2)解析式是分式时,自变量的取值应使分母不为0;
(3)解析式是平方根时,自变量取值范围应使被开方数大于 或等于0;
(4)解决实际问题时,必须既符合理论又满足实际,特别注意:不要先化简关系式再求取值范围.
当 x = 3 时,求下列函数的函数值:
解: (1)当x=3时,y=2x+4=2×3+4=10.
(2)当x=3时,y=-2x2=-2×32=-18.
(3)当x=3时,
(4)当x=3时,
例2
(1)y=2x+4; (2)y=-2x2;
(3) (4)
例题与练习
范例
求下列函数中自变量x的取值范围:
解:(1)任意实数;
(2)任意实数;
(3)x≠-2;
(4)x≥2.
解析:根据题意得x-1≥0且 x-2≠0,
解得x≥1且 x ≠2.
故答案为x≥1且 x ≠2.
x≥1且x≠2
仿例
函数y = 有意义,则自变量x的取值范围是
__________________.
1.求下列函数中自变量x的取值范围:
解:(1)x为全体实数.
(2)x≠4.
(3)x≥5.
(4)x为全体实数.
练习
解:(1)当x=9时,y=-2;当x=10时,
(2)当x=9时, ;当x=10时,
2.求下列函数当x=9和x=10的函数值:
一个游泳池内有水 300 m3,现打开排水管以每时 25 m3 排出量排水.
(1)写出游泳池内剩余水量Q (m3)与排水时间t(h)之间的函数表达式;
(2)写出自变量 t 的取值范围;
在实际问题中求自变量取值范围
例3
解:(1)排水后的剩水量Q是排水时间t的函数,有
Q=-25t+300;
(2)由于池中共有300m3水,每时排25m3,全部排完只需300÷25=12(h),故自变量t的取值范围是0≤t≤12.
(3)开始排水5 h 后,游泳池中还有多少水?
(4)当游泳池中还剩 150 m3 水时,已经排水多少时间?
解:(3)当t=5,代入上式得Q=-5×25+300=175(m3),
即排水5h后,池中还有水175m3.
(4)当Q=150时,由150=-25t+300,得t=6,即已经排水6h.
范例
水箱内原有水200升,7点30分打开水龙头,以2升/分的速度放水,设经t分钟时,水箱内存水y升.
(1)求y关于t的函数关系式和自变量的取值范围;
(2)7∶55时,水箱内还有多少水?
(3)几点几分水箱内的水恰好放完?
解:(1)y=200-2t,
(2)即t=25,y=200-2×25,
(3)当y=0,即200-2t=0,t=100,
∵水100分钟放完,
∴自变量取值范围为0≤t≤100;
7∶55时,水箱还有150升水;
7∶30+1时40分=9点10分,故9点10分水箱水恰好放完.
仿例
如图,在靠墙(墙长为18m)的地方围建一个长方形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m.
(1)试写出养鸡场平行于墙的长y(m)与垂直于墙的长x(m)的函数关系式;
(2)求自变量x的取值范围.
解:(1)y=35-2x;
(2)∵y=35-2x≤18,
∴x≥8.5,
∵35-2x>0,x<17.5,
∴自变量x取值范围是8.5≤x<17.5.
在实际问题中确定自变量的取值范围,主
要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
知识归纳
实际问题中自变量的取值范围
求函数值
范例1:
函数y= ,当x=1时,y= ;当x=3时,y= .
3
-3
范例2:
已知函数y= ,当x=-4时,y= .
0
例题与练习
范例3:
如图,根据流程图中的程序,当输出数值y=5时,输入数值x是( )
C
随堂练习
1.一列火车以80km/h的速度匀速行驶.
(1)写出它行驶的路程 s km与时间 t h之间的函数表达式;
(2)当t=10时,s是多少?
解:(1)s=80t;
(2)当t=10时,s=800.
2.求下列函数中自变量x的取值范围:
x ≠0
x ≠-1
x≥0
x为一切实数
x≥2
x为一切实数
3.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) 10 20 30
y(单位:万元/台) 60 55 50
则y与x之间的解析式是( )
A.y=80- 2x B.y=40+ 2x
D.y=60-
C
C. y=65-
课堂小结
函数的表示方法
列表法、解析法和图象法
自变量的取值范围
使含自变量的等式有意义
使实际问题有意义
