沪科版八年级数学上册12.1.3 函数的表示方法-图象法 课件 (共17张PPT)
文档属性
| 名称 | 沪科版八年级数学上册12.1.3 函数的表示方法-图象法 课件 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 11:11:29 | ||
图片预览




文档简介
(共17张PPT)
第十二章 一次函数
12.1 函数
第3课时 函数的表示方法—图象法
旧知回顾
导入新课
1.函数有哪几种表示法?
答:解析法、列表法、图象法.
2.右图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化.
试回答:一天中什么时候温度最高?什么时候温度最低?什么时段温度不断上升?什么时段温度不断下降?
探究新知
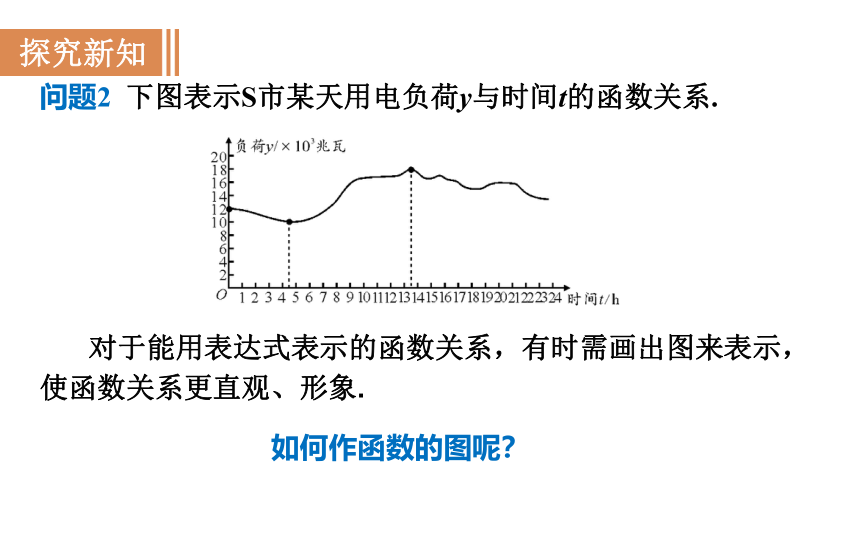
问题2 下图表示S市某天用电负荷y与时间t的函数关系.
对于能用表达式表示的函数关系,有时需画出图来表示,使函数关系更直观、形象.
如何作函数的图呢?
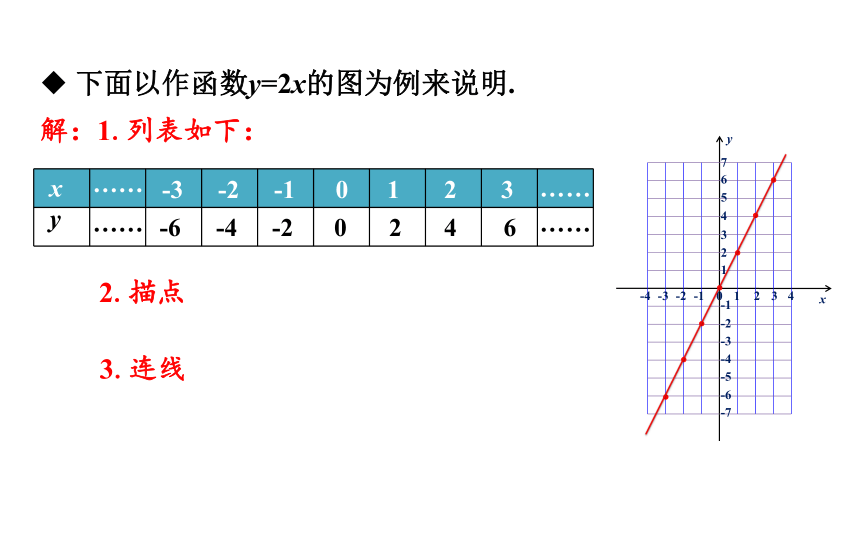
下面以作函数y=2x的图为例来说明.
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
解:1.列表如下:
x
y
……
……
-3
-6
-2
-4
-1
-2
0
0
1
2
2
4
3
6
……
……
2.描点
3.连线
由函数表达式画图象的一般步骤:
知识归纳
1.列表:分析函数自变量的取值范围,取自变量的一些值(间隔相同),算出y的对应值;
2.描点:以表中对应值为坐标,在坐标系内描出相应的点;
3.连线:分析函数图象的发展趋势(是直线还是曲线,有限还是无限)按照自变量由小到大的顺序,用平滑的曲线连接所描的各点,即得图象.
注意:描出的点越多,图象就越精确.
例1
例题与练习
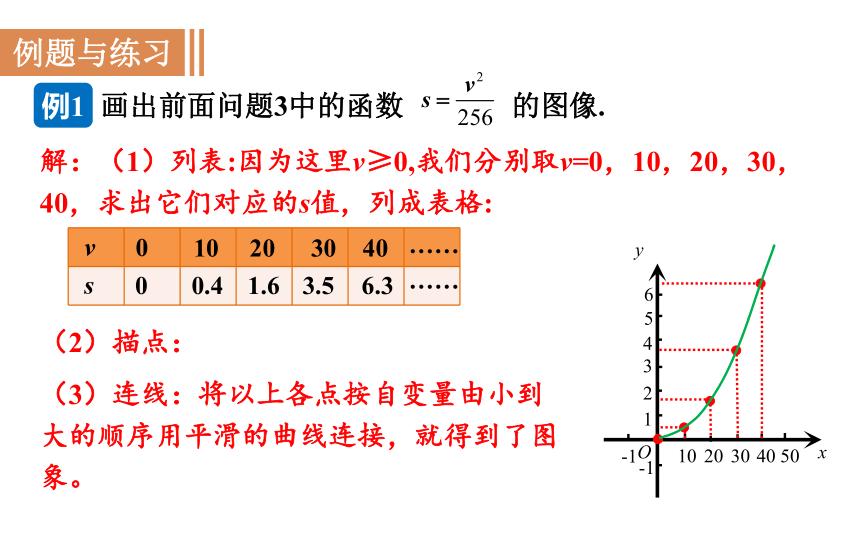
画出前面问题3中的函数 的图像.
解:(1)列表:因为这里v≥0,我们分别取v=0,10,20,30,40,求出它们对应的s值,列成表格:
v
s
0
0
10
0.4
20
1.6
30
3.5
40
6.3
……
……
O
x
y
10
20
30
40
50
-1
3
1
4
2
5
-1
6
(2)描点:
(3)连线:将以上各点按自变量由小到大的顺序用平滑的曲线连接,就得到了图象。
范例
有一个水箱,容积为500升,水箱内原有水200升.现向水箱内加水,加满后停止加水,若每分钟加水10升,加水t分钟后,水箱内的水量为Q升.
(1)写出Q(升)关于t(分钟)的函数解析式;
(2)求自变量t的取值范围;
(3)画出函数图象.
解:(1)水箱内的水量是在200升的基础上,再加新注入的水量,因此Q=200+10t;
(2)往此水箱内注水最多加500-20010=30(分钟),
∴0≤t≤30;
在平面直角坐标系中描点、连线,得到函数图象如图.
(3)列表
t(分钟)
0
5
10
15
20
25
30
200
250
300
350
400
450
500
Q(升)
t(分钟)
0
5
10
15
20
25
30
Q(升)
50
100
150
200
250
300
350
400
450
500
仿例
画出函数y=x+2的图象.
(1)判断点(2,-1)是否在函数图象上;
(2)利用图象分析y随x的变化情况;
(3)利用图象观察,当x满足什么条件时y=0.
解:图略.
(2) y随x增大而增大;
(3) 当x=-2时,y=0.
(1) 不在,当x=2时,y=2+2=4,4≠-1,
∴点(2,-1)不在函数图象上;
从函数图象中观察信息
范例
右图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.
根据图象回答下列问题:
(1)菜地离小明家多远?小明走到菜地用了多长时间?
(2)小明给菜地浇水用了多少时间?
(2)25-15=10分钟
解:(1)1.1千米,15分钟
(3)菜地离玉米地多远?小明从菜地到玉米地用了多长时间?
(4)小明给玉米地锄草用了多长时间?
(5)玉米地离小明家多远?小明从玉米地走回家平均速度是多少?
(5)2千米,2000÷(80-55)=80米/分.
解:(3)2-1.1=0.9千米,37-25=12分钟
(4)55-37=18分钟
仿例
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )
A.甲、乙两人的速度相同
B.甲先到达终点
C.乙用的时间短
D.乙比甲跑的路程多
B
仿例2
如图,爸爸从家(点O)出发,沿着扇形AOB上OA→弧AB→BO的路径匀速散步.设爸爸距家(点O)的距离为s,散步的时间为t,则下列图形中能大致刻画s与t之间函数关系图象的是( )
C
随堂练习
1.画出函数y=-2x的图像(先列表,然后描点、连线)
解:(1)列表:
(3)连线:
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
(2)描点:
x
y
……
……
-3
6
-2
4
-1
2
0
0
1
-2
2
-4
3
-6
……
……
2.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
描点、连线:
用描点法画函数l=3a的图象.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).
a
l
1
3
2
6
3
9
4
12
……
……
……
……
O
2
x
y
1
2
3
4
5
8
6
4
10
12
3.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离是时间的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
是
s = 200-25t
列表:
解析:船速度为
(200-150)÷2=25m/min,
s=200-25t
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
课堂小结
函数关系的方法有三种:
1.解析法——用数学式子表示函数的关系.
2.列表法——通过列表给出自变量与函数的对应关系.
3.图象法——把自变量作为点的横坐标,对应的函数值作为点的纵坐标,在直角坐标系内描出对应的点,所有这些点的集合,叫做这个函数的图象.用图象来表示两个变量之间的函数关系叫做图象法.
画函数的图象要经过(1)列表;(2)描点; (3)连线.
第十二章 一次函数
12.1 函数
第3课时 函数的表示方法—图象法
旧知回顾
导入新课
1.函数有哪几种表示法?
答:解析法、列表法、图象法.
2.右图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化.
试回答:一天中什么时候温度最高?什么时候温度最低?什么时段温度不断上升?什么时段温度不断下降?
探究新知
问题2 下图表示S市某天用电负荷y与时间t的函数关系.
对于能用表达式表示的函数关系,有时需画出图来表示,使函数关系更直观、形象.
如何作函数的图呢?
下面以作函数y=2x的图为例来说明.
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
解:1.列表如下:
x
y
……
……
-3
-6
-2
-4
-1
-2
0
0
1
2
2
4
3
6
……
……
2.描点
3.连线
由函数表达式画图象的一般步骤:
知识归纳
1.列表:分析函数自变量的取值范围,取自变量的一些值(间隔相同),算出y的对应值;
2.描点:以表中对应值为坐标,在坐标系内描出相应的点;
3.连线:分析函数图象的发展趋势(是直线还是曲线,有限还是无限)按照自变量由小到大的顺序,用平滑的曲线连接所描的各点,即得图象.
注意:描出的点越多,图象就越精确.
例1
例题与练习
画出前面问题3中的函数 的图像.
解:(1)列表:因为这里v≥0,我们分别取v=0,10,20,30,40,求出它们对应的s值,列成表格:
v
s
0
0
10
0.4
20
1.6
30
3.5
40
6.3
……
……
O
x
y
10
20
30
40
50
-1
3
1
4
2
5
-1
6
(2)描点:
(3)连线:将以上各点按自变量由小到大的顺序用平滑的曲线连接,就得到了图象。
范例
有一个水箱,容积为500升,水箱内原有水200升.现向水箱内加水,加满后停止加水,若每分钟加水10升,加水t分钟后,水箱内的水量为Q升.
(1)写出Q(升)关于t(分钟)的函数解析式;
(2)求自变量t的取值范围;
(3)画出函数图象.
解:(1)水箱内的水量是在200升的基础上,再加新注入的水量,因此Q=200+10t;
(2)往此水箱内注水最多加500-20010=30(分钟),
∴0≤t≤30;
在平面直角坐标系中描点、连线,得到函数图象如图.
(3)列表
t(分钟)
0
5
10
15
20
25
30
200
250
300
350
400
450
500
Q(升)
t(分钟)
0
5
10
15
20
25
30
Q(升)
50
100
150
200
250
300
350
400
450
500
仿例
画出函数y=x+2的图象.
(1)判断点(2,-1)是否在函数图象上;
(2)利用图象分析y随x的变化情况;
(3)利用图象观察,当x满足什么条件时y=0.
解:图略.
(2) y随x增大而增大;
(3) 当x=-2时,y=0.
(1) 不在,当x=2时,y=2+2=4,4≠-1,
∴点(2,-1)不在函数图象上;
从函数图象中观察信息
范例
右图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.
根据图象回答下列问题:
(1)菜地离小明家多远?小明走到菜地用了多长时间?
(2)小明给菜地浇水用了多少时间?
(2)25-15=10分钟
解:(1)1.1千米,15分钟
(3)菜地离玉米地多远?小明从菜地到玉米地用了多长时间?
(4)小明给玉米地锄草用了多长时间?
(5)玉米地离小明家多远?小明从玉米地走回家平均速度是多少?
(5)2千米,2000÷(80-55)=80米/分.
解:(3)2-1.1=0.9千米,37-25=12分钟
(4)55-37=18分钟
仿例
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )
A.甲、乙两人的速度相同
B.甲先到达终点
C.乙用的时间短
D.乙比甲跑的路程多
B
仿例2
如图,爸爸从家(点O)出发,沿着扇形AOB上OA→弧AB→BO的路径匀速散步.设爸爸距家(点O)的距离为s,散步的时间为t,则下列图形中能大致刻画s与t之间函数关系图象的是( )
C
随堂练习
1.画出函数y=-2x的图像(先列表,然后描点、连线)
解:(1)列表:
(3)连线:
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
(2)描点:
x
y
……
……
-3
6
-2
4
-1
2
0
0
1
-2
2
-4
3
-6
……
……
2.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
描点、连线:
用描点法画函数l=3a的图象.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).
a
l
1
3
2
6
3
9
4
12
……
……
……
……
O
2
x
y
1
2
3
4
5
8
6
4
10
12
3.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离是时间的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
是
s = 200-25t
列表:
解析:船速度为
(200-150)÷2=25m/min,
s=200-25t
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
课堂小结
函数关系的方法有三种:
1.解析法——用数学式子表示函数的关系.
2.列表法——通过列表给出自变量与函数的对应关系.
3.图象法——把自变量作为点的横坐标,对应的函数值作为点的纵坐标,在直角坐标系内描出对应的点,所有这些点的集合,叫做这个函数的图象.用图象来表示两个变量之间的函数关系叫做图象法.
画函数的图象要经过(1)列表;(2)描点; (3)连线.
