沪科版八年级数学上册 12.2.4 一次函数的应用 课件(共23张PPT)
文档属性
| 名称 | 沪科版八年级数学上册 12.2.4 一次函数的应用 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 827.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 11:46:05 | ||
图片预览








文档简介
(共23张PPT)
第十二章 一次函数
12.2 一次函数
第4课时 一次函数的应用
导入新课
问题 某市出租车的计价方式是:开始3km内收费6元,以后每增加1km(不足1km,以1km计)加收1元.
(1)写出乘车路程xkm与收费y元的关系式;
(2)小明乘车5.6km,应付多少钱?
(3)小飞乘车付了15元,他乘车走了多少路?
解:(1)y=x+3;
(2)9元;
(3)12km.
探究新知
分段函数的应用
例 为节约用水,某城市制定以下用水收费标准:每户每月用水不超过8m3时,每立方米收取1元外加0.3元的污水处理费;超过8m3时,超过部分每立方米收取1.5元外加1.2元的污水处理费.设一户每月用水量为xm3,应缴水费y元.
(1)给出y关于x的函数关系式;
(2)画出上述函数图象;
(3)当该市一户某月的用水量为x=5m3或x=10m3时,求其应缴的水费;
(4)该市一户某月缴水费26.6元,求该户这个月用水量.
分析:
(1)x≤8时,每立方米收费(1+0.3)元
(2)x>8时,超过的部分每立方米收费(1.5+1.2)元
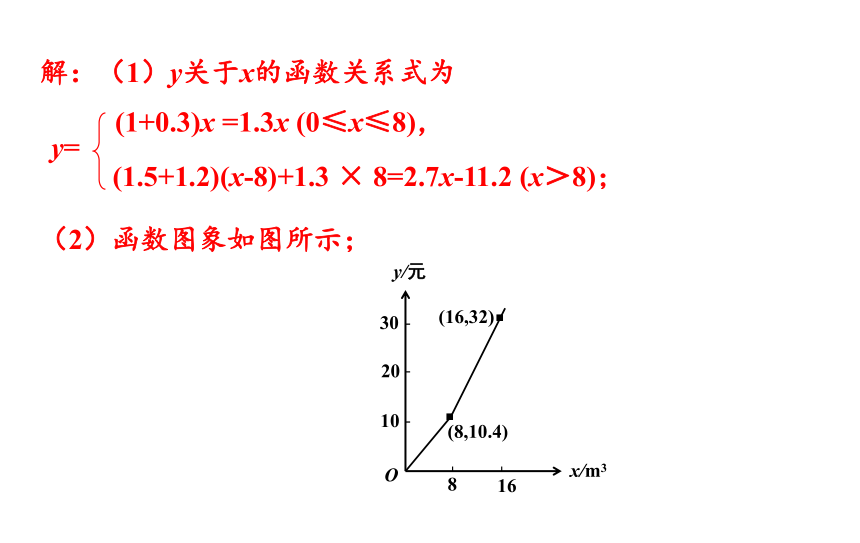
解:(1)y关于x的函数关系式为
30
20
10
8
16
O
y/元
x/m3
(2)函数图象如图所示;
(1+0.3)x =1.3x (0≤x≤8),
(1.5+1.2)(x-8)+1.3 × 8=2.7x-11.2 (x>8);
y=
.
.
(8,10.4)
(16,32)
(3)当x=5 m3时,y=1.3×5=6.5(元);
(4)y=26.6>1.3×8,可知该户这月用水超过8m3,
当x=10m3时,y=2.7×10-11.2=15.8(元).
即当用水量为5m3时,该户应缴水费6.5元;
当用水量为10m3时,该户应缴水费15.8元.
因此,2.7x-11.2=26.6,
解方程,得 x=14.
即该户本月用水量为14m3.
知识归纳
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数.
(1)分段函数是一个整体,这个整体是一个函数.
(2)函数y在x的某个范围内可能是特殊函数,如一次函数.
(3)由于问题的不同,分段函数也可能在自变量某范围内不是一次函数而是其他形式的函数,在这里我们不予讨论.
仿例1
例题与练习
如图中的直线ABC,为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(分钟)之间的函数关系式的图象.
当t≥2时,该图象的解析式为 ;从图象中可知,通话2分钟需付电话费 元;通话7分钟需付电话费 元.
y=t-0.6
1.4
6.4
为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数关系式:
仿例2
(2)当每月用电量不超过50度时,收费标准是 元/度;
当每月用电量超过50度时,超过的部分的收费标准是
元/度.
0.5
0.9
利用一次函数进行方案选择
例 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
分析:假设该单位参加旅游人数为x,按甲旅行社的优惠条
件,应付费用80x(元);按乙旅行社的优惠条件,应付费用
(60x+1000)(元).问题变为比较80x 与60x+1000 的大小了.
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x(元);选乙旅行社,应付(60x+1000)(元).
记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
y/元
800
1600
3200
2400
4000
4800
5600
观察图象,可知:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
x/人
50
60
O
10
20
30
40
70
y1= 80x
y2= 60x+1000
解法二:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
-200
-400
-600
-800
-1000
y
它与x轴交点为(50,0) 由图知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2.
O
20
40
60
x
y= 20x-1000
解法三:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50.
所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;
利用图象法解决实际生活中的方案选择问题,一般按如下步骤进行:
知识归纳
(1)用已知条件求出实际问题的函数关系式;
(2)在同一直角坐标系中,作出所得函数的图象;
(3)观察图象找出这两个一次函数图象的交点坐标;
(4)根据交点坐标来选择合适的方案.
典例
某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系式如图.
(1)有月租时的收费方式是_______(选填“①”或“②”),月租费是_______元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
(2) 设y①=k1x+30(k1≠0),y②=k2x(k2≠0),
解:(1)①;
30;
将(500,80)代入y①=k1x+30(k1≠0),
得500k1+30=80,
∴k1=0.1.将(500,100)代入y②=k2x(k2≠0),
得500k2=100,
∴k2=0.2.
故①、②两种收费方式中y与自变量x之间的函数表达式分别为y①=0.1x+30,y②=0.2x;
(3)由y①=y②,
得0.1x+30=0.2x,解得x=300.
当x=300时,y=60.
由图可知,
当通讯时间在300分钟以内时,选择收费方式②实惠;
当通讯时间超过300分钟时,选择收费方式①实惠;
当通讯时间等于300分钟时,选择收费方式①、②一样实惠.
1.如图,l1反映某公司产品的销售收入与销售量的关系,l2反映该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时的销售量( )
A.小于4件 B.大于4件
C.等于4件 D.大于或等于4件
B
随堂练习
2.某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为yA元和yB元.
(1)分别求出yA、yB与x之间的函数关系式;
解:yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
(2)试讨论A、B两地中,哪个的运费较少;
解:∵yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
∴当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少;
(3)考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
解:设两地运费之和为y元,
则y=yA+yB=(-5x+5000)+(3x+4680)=-2x+9680.
由题意得yB=3x+4680≤4830,解得 x≤50.
∵y随x的增大而减小,x最大为50,
∴y最小=-2×50+9680=9580.
∴在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元.
3. 某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费为0.36元/min;
B方案: 零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
解: (1) A方案: y = 25+0.36t(t≥0),
y = 0.5t(t≥0).
B方案:
(2)这两个函数的图象如下:
O
5
15
10
●
5
10
y
t
30
15
25
35
●
y = 25+0.36t(t≥0)
O
1
3
2
1
2
3
y
t
●
y = 0.5t(t≥0)
●
解:当t=300时,
A方案:
y = 25+0.36t=25+0.36×300=133(元);
所以此时采用A方案比较合算.
(3)若林先生每月通话300 min,他选择哪种付费方式比较合算?
B方案:
y = 0.5t=0.5×300=150(元).
从数学的角度分析数学问题,建立函数模型
一次函数的应用
课堂小结
列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
结合实际需求,选择最佳方案
第十二章 一次函数
12.2 一次函数
第4课时 一次函数的应用
导入新课
问题 某市出租车的计价方式是:开始3km内收费6元,以后每增加1km(不足1km,以1km计)加收1元.
(1)写出乘车路程xkm与收费y元的关系式;
(2)小明乘车5.6km,应付多少钱?
(3)小飞乘车付了15元,他乘车走了多少路?
解:(1)y=x+3;
(2)9元;
(3)12km.
探究新知
分段函数的应用
例 为节约用水,某城市制定以下用水收费标准:每户每月用水不超过8m3时,每立方米收取1元外加0.3元的污水处理费;超过8m3时,超过部分每立方米收取1.5元外加1.2元的污水处理费.设一户每月用水量为xm3,应缴水费y元.
(1)给出y关于x的函数关系式;
(2)画出上述函数图象;
(3)当该市一户某月的用水量为x=5m3或x=10m3时,求其应缴的水费;
(4)该市一户某月缴水费26.6元,求该户这个月用水量.
分析:
(1)x≤8时,每立方米收费(1+0.3)元
(2)x>8时,超过的部分每立方米收费(1.5+1.2)元
解:(1)y关于x的函数关系式为
30
20
10
8
16
O
y/元
x/m3
(2)函数图象如图所示;
(1+0.3)x =1.3x (0≤x≤8),
(1.5+1.2)(x-8)+1.3 × 8=2.7x-11.2 (x>8);
y=
.
.
(8,10.4)
(16,32)
(3)当x=5 m3时,y=1.3×5=6.5(元);
(4)y=26.6>1.3×8,可知该户这月用水超过8m3,
当x=10m3时,y=2.7×10-11.2=15.8(元).
即当用水量为5m3时,该户应缴水费6.5元;
当用水量为10m3时,该户应缴水费15.8元.
因此,2.7x-11.2=26.6,
解方程,得 x=14.
即该户本月用水量为14m3.
知识归纳
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数.
(1)分段函数是一个整体,这个整体是一个函数.
(2)函数y在x的某个范围内可能是特殊函数,如一次函数.
(3)由于问题的不同,分段函数也可能在自变量某范围内不是一次函数而是其他形式的函数,在这里我们不予讨论.
仿例1
例题与练习
如图中的直线ABC,为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(分钟)之间的函数关系式的图象.
当t≥2时,该图象的解析式为 ;从图象中可知,通话2分钟需付电话费 元;通话7分钟需付电话费 元.
y=t-0.6
1.4
6.4
为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数关系式:
仿例2
(2)当每月用电量不超过50度时,收费标准是 元/度;
当每月用电量超过50度时,超过的部分的收费标准是
元/度.
0.5
0.9
利用一次函数进行方案选择
例 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
分析:假设该单位参加旅游人数为x,按甲旅行社的优惠条
件,应付费用80x(元);按乙旅行社的优惠条件,应付费用
(60x+1000)(元).问题变为比较80x 与60x+1000 的大小了.
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x(元);选乙旅行社,应付(60x+1000)(元).
记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
y/元
800
1600
3200
2400
4000
4800
5600
观察图象,可知:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
x/人
50
60
O
10
20
30
40
70
y1= 80x
y2= 60x+1000
解法二:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
-200
-400
-600
-800
-1000
y
它与x轴交点为(50,0) 由图知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2.
O
20
40
60
x
y= 20x-1000
解法三:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50.
所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;
利用图象法解决实际生活中的方案选择问题,一般按如下步骤进行:
知识归纳
(1)用已知条件求出实际问题的函数关系式;
(2)在同一直角坐标系中,作出所得函数的图象;
(3)观察图象找出这两个一次函数图象的交点坐标;
(4)根据交点坐标来选择合适的方案.
典例
某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系式如图.
(1)有月租时的收费方式是_______(选填“①”或“②”),月租费是_______元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
(2) 设y①=k1x+30(k1≠0),y②=k2x(k2≠0),
解:(1)①;
30;
将(500,80)代入y①=k1x+30(k1≠0),
得500k1+30=80,
∴k1=0.1.将(500,100)代入y②=k2x(k2≠0),
得500k2=100,
∴k2=0.2.
故①、②两种收费方式中y与自变量x之间的函数表达式分别为y①=0.1x+30,y②=0.2x;
(3)由y①=y②,
得0.1x+30=0.2x,解得x=300.
当x=300时,y=60.
由图可知,
当通讯时间在300分钟以内时,选择收费方式②实惠;
当通讯时间超过300分钟时,选择收费方式①实惠;
当通讯时间等于300分钟时,选择收费方式①、②一样实惠.
1.如图,l1反映某公司产品的销售收入与销售量的关系,l2反映该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时的销售量( )
A.小于4件 B.大于4件
C.等于4件 D.大于或等于4件
B
随堂练习
2.某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为yA元和yB元.
(1)分别求出yA、yB与x之间的函数关系式;
解:yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
(2)试讨论A、B两地中,哪个的运费较少;
解:∵yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
∴当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少;
(3)考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
解:设两地运费之和为y元,
则y=yA+yB=(-5x+5000)+(3x+4680)=-2x+9680.
由题意得yB=3x+4680≤4830,解得 x≤50.
∵y随x的增大而减小,x最大为50,
∴y最小=-2×50+9680=9580.
∴在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元.
3. 某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费为0.36元/min;
B方案: 零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
解: (1) A方案: y = 25+0.36t(t≥0),
y = 0.5t(t≥0).
B方案:
(2)这两个函数的图象如下:
O
5
15
10
●
5
10
y
t
30
15
25
35
●
y = 25+0.36t(t≥0)
O
1
3
2
1
2
3
y
t
●
y = 0.5t(t≥0)
●
解:当t=300时,
A方案:
y = 25+0.36t=25+0.36×300=133(元);
所以此时采用A方案比较合算.
(3)若林先生每月通话300 min,他选择哪种付费方式比较合算?
B方案:
y = 0.5t=0.5×300=150(元).
从数学的角度分析数学问题,建立函数模型
一次函数的应用
课堂小结
列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
结合实际需求,选择最佳方案
