沪科版八年级数学上册12.2.5 一次函数与一次方程、一次不等式 课件 (共23张PPT)
文档属性
| 名称 | 沪科版八年级数学上册12.2.5 一次函数与一次方程、一次不等式 课件 (共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 245.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 11:29:56 | ||
图片预览






文档简介
(共23张PPT)
第十二章 一次函数
12.2 一次函数
第5课时 一次函数与一次方程、一次不等式
导入新课
旧知回顾
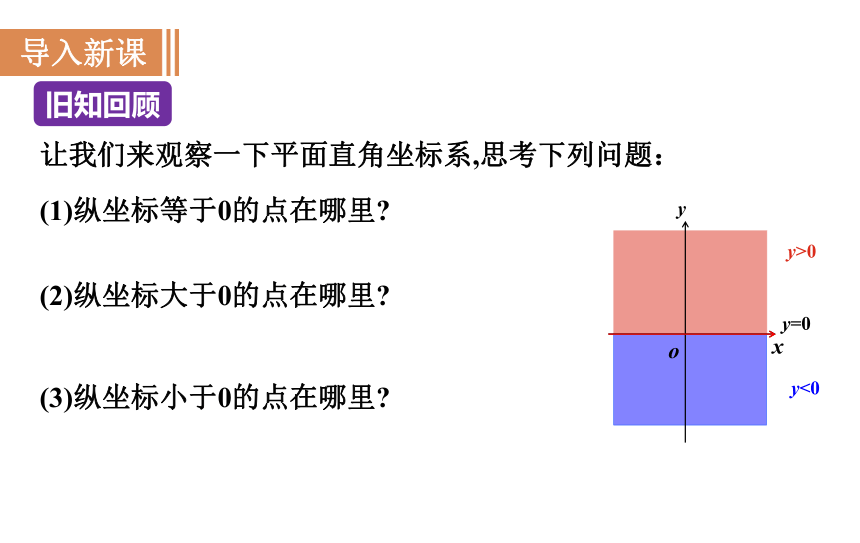
y<0
y>0
让我们来观察一下平面直角坐标系,思考下列问题:
(1)纵坐标等于0的点在哪里
(2)纵坐标大于0的点在哪里
(3)纵坐标小于0的点在哪里
x
y
o
y=0
探究新知
问题1 已知一次函数y=2x+6
(1)画出函数图象,并求它与x轴交点的坐标.
(2)观察图象,判断x取什么值时,函数y的值等于零?
(3)函数y=2x+6的图象与x轴交点的横坐标与一次方程2x+6=0的解有何关系?
解:(1)如图,与x轴交点坐标为(-3,0);
O
x
y
y=2x+6
A(0,6)
B(-3,0)
(2)x取-3时,函数y的值等于零;
(3)一次函数y=2x+6的图象与x轴交点的横坐标x=-3就是方程2x+6=0的解.
一次函数与一元一次方程的关系
知识归纳
一次函数与一元一次方程的关系
一般地,一元一次方程 kx+b=0 的解就是一次函数y=kx+b的图象与x轴交点的横坐标.
范例
利用函数图象解方程:3x-2=x+4.
解:由3x-2=x+4得2x-6=0.
令y=2x-6,画出函数y=2x-6的图象(如右图).
分析:先将方程化为kx+b=0的形式,再在坐标系中画出函数y=kx+b的图象,然后观察出直线y=kx+b与x轴的交点坐标,从而确定所求x的值.
由图象可以看出直线y=2x-6与x轴的交点坐标为(3,0),
例题与练习
-1
-2
-3
-4
-5
y
-6
O
1
3
5
x
y= 2x-6
2
4
所以原方程的解就是该交点的横坐标,即x=3.
仿例1
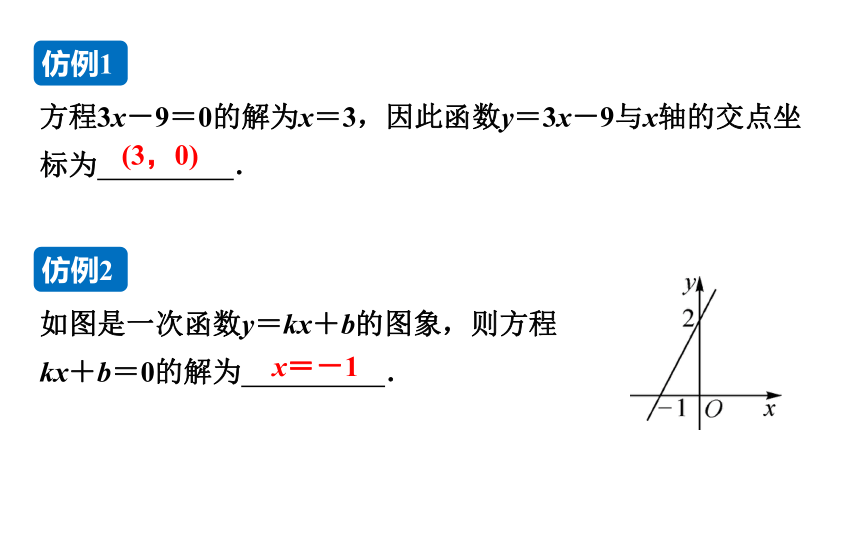
方程3x-9=0的解为x=3,因此函数y=3x-9与x轴的交点坐标为 .
如图是一次函数y=kx+b的图象,则方程kx+b=0的解为 .
(3,0)
x=-1
仿例2
一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=3的解为 .
x=2
仿例3
1.画出一次函数 y=-2x-6 的图象,结合图象求:
A(-3,0)
(1)x______时,y=0;
(2)x______时,y>0;
(3)x______时,y<0;
(4)x______时,y>6;
B(-6,6)
=-3
<-3
>-3
<-6
练习
y=-2x-6
6
4
2
-2
-4
y
-6
O
-4
4
x
-2
2
-6
C(0,-6)
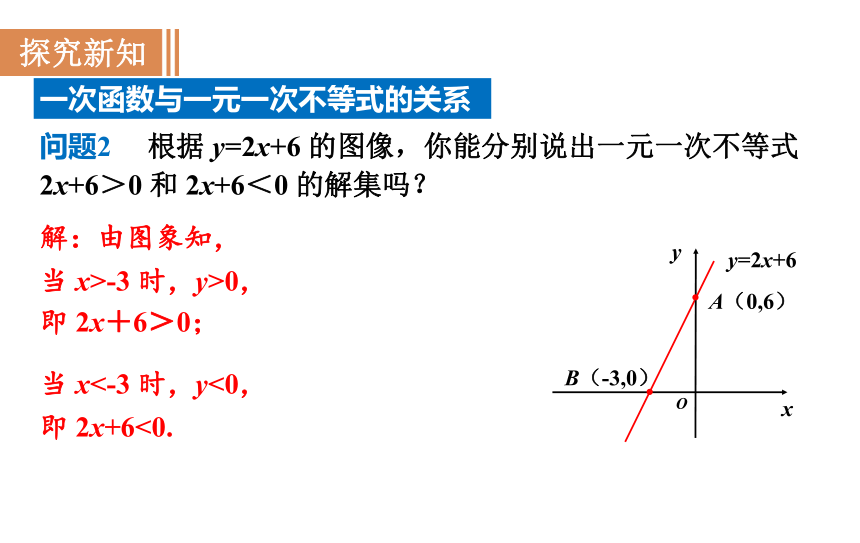
问题2 根据 y=2x+6 的图像,你能分别说出一元一次不等式 2x+6>0 和 2x+6<0 的解集吗?
O
x
y
y=2x+6
A(0,6)
B(-3,0)
解:由图象知,
当 x>-3 时,y>0,
即 2x+6>0;
当 x<-3 时,y<0,
即 2x+6<0.
一次函数与一元一次不等式的关系
探究新知
任何一个一元一次不等式都可以转化为kx+b>0(或kx+b<0)的形式,所以解一元一次不等式kx+b>0(或kx+b<0),就是求使一次函数y=kx+b(k,b为常数,且k≠0)取正值(或负值)时x的取值范围.
知识归纳
一次函数与一元一次不等式的关系
例 画出函数 y=-3x+6 的图象,结合图象:
(1)求方程 -3x+6=0 的解;
O
x
y
y=-3x+6
A(0,6)
B(2,0)
解:函数 y=-3x+6 的图象如图所示,图象与x轴的交点是(2,0).
例题与练习
所以方程 -3x+6=0 的解就是交点B的横坐标:x=2.
O
x
y=-3x+6
A(0,6)
B(2,0)
解:结合图象可知,y>0时x的取值范围是 x<2; y<0时x的取值范围是 x>2.
所以,不等式-3x+6>0的解集是x<2,不等式-3x+6<0的解集是x>2.
(2)求不等式-3x+6>0和-3x+6<0的解集.
范例1
已知一次函数y=kx+b的图象如图所示,当x<-4时,y的取值范围是 ( )
A.y>0 B.y<0
C.-2B
例题与练习
B
若函数y=ax+b(a≠0)的图象如图所示,则不等式
ax+b≥0的解集是( )
A.x≥3 B.x≤3 C.x=3 D.x≥
范例2
已知一次函数y=kx+b(k、b是常数,且k≠0),x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是 .
x -2 -1 0 1 2 3
y 3 2 1 0 -1 -2
x>1
仿例1
如图,直线y=kx+b分别交x轴和y轴于点A、B.
(1)关于x的方程kx+b=0的解是什么?
(2)当x为何值时,0(3)当x为何值时,y>1
解:(1)x=-2;
(2)由图可知,
(3)把点(-2,0),(0,3)代入y=kx+b求得解析式为
y= x+3,
仿例2
当y= x+3>1时,x> .
当y>0时,x>-2;
当y<3时,x<0.∴-22.画出函数 y=3x-9 的图象;
(1)求方程 3x-9=0 的解;
(2)求不等式 3x-9≤0 的解集;
(3)当 y=3 时,求x的值;
(4)当 y>3 时,求x的范围.
O
x
y
y=3x-9
A(0,-9)
B(3,0)
解:图象如图所示,
C(4,3)
(1)x=3;
练习
(3)x=4;
(2)x≤3;
(4)x>4.
随堂练习
1.一次函数y=-x+2的图象如图,你能说出-x+2<0的解集吗?
x
y
0
y=-x+2
2
解:x>2
2.一次函数y=kx+b的图象如图,你能说出kx+b<0的解集吗?
x
y
0
y=kx+b
-4
解:x < -4
3.利用图象解一元一次方程x+3=0.
解:作y=x+3图象如右图.
x
3
y=x+3
O
y
3
由图象知y=x+3交x轴于(-3,0),
所以原方程的解为x = 3 .
4.用画函数图象的方法解不等式5x+4<2x+10.
解:原不等式化为3x -6<0,
画出直线y = 3x -6(如图).
可以看出,当x<2 时这条直线上的点在x轴的下方,
即这时y = 3x -6 <0,
所以不等式的解集为x<2.
y=3x-6
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
即5x+4 <2x +10的解集为x<2.
解:画出两个函数
y=5x 1和y=2x+5的图象.
由图象知,两直线交于点 (2,9),所以原方程的解为 x=2.
O
y=5x 1
y=2x+5
9
2
x
y
5.利用函数图象求x的值:
5x 1= 2x+5.
课堂小结
一次函数与一元一次方程、一元一次不等式
解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式可以看作:当一次函数的函数值大(小)于0时,求自变量相应的取值范围.
第十二章 一次函数
12.2 一次函数
第5课时 一次函数与一次方程、一次不等式
导入新课
旧知回顾
y<0
y>0
让我们来观察一下平面直角坐标系,思考下列问题:
(1)纵坐标等于0的点在哪里
(2)纵坐标大于0的点在哪里
(3)纵坐标小于0的点在哪里
x
y
o
y=0
探究新知
问题1 已知一次函数y=2x+6
(1)画出函数图象,并求它与x轴交点的坐标.
(2)观察图象,判断x取什么值时,函数y的值等于零?
(3)函数y=2x+6的图象与x轴交点的横坐标与一次方程2x+6=0的解有何关系?
解:(1)如图,与x轴交点坐标为(-3,0);
O
x
y
y=2x+6
A(0,6)
B(-3,0)
(2)x取-3时,函数y的值等于零;
(3)一次函数y=2x+6的图象与x轴交点的横坐标x=-3就是方程2x+6=0的解.
一次函数与一元一次方程的关系
知识归纳
一次函数与一元一次方程的关系
一般地,一元一次方程 kx+b=0 的解就是一次函数y=kx+b的图象与x轴交点的横坐标.
范例
利用函数图象解方程:3x-2=x+4.
解:由3x-2=x+4得2x-6=0.
令y=2x-6,画出函数y=2x-6的图象(如右图).
分析:先将方程化为kx+b=0的形式,再在坐标系中画出函数y=kx+b的图象,然后观察出直线y=kx+b与x轴的交点坐标,从而确定所求x的值.
由图象可以看出直线y=2x-6与x轴的交点坐标为(3,0),
例题与练习
-1
-2
-3
-4
-5
y
-6
O
1
3
5
x
y= 2x-6
2
4
所以原方程的解就是该交点的横坐标,即x=3.
仿例1
方程3x-9=0的解为x=3,因此函数y=3x-9与x轴的交点坐标为 .
如图是一次函数y=kx+b的图象,则方程kx+b=0的解为 .
(3,0)
x=-1
仿例2
一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=3的解为 .
x=2
仿例3
1.画出一次函数 y=-2x-6 的图象,结合图象求:
A(-3,0)
(1)x______时,y=0;
(2)x______时,y>0;
(3)x______时,y<0;
(4)x______时,y>6;
B(-6,6)
=-3
<-3
>-3
<-6
练习
y=-2x-6
6
4
2
-2
-4
y
-6
O
-4
4
x
-2
2
-6
C(0,-6)
问题2 根据 y=2x+6 的图像,你能分别说出一元一次不等式 2x+6>0 和 2x+6<0 的解集吗?
O
x
y
y=2x+6
A(0,6)
B(-3,0)
解:由图象知,
当 x>-3 时,y>0,
即 2x+6>0;
当 x<-3 时,y<0,
即 2x+6<0.
一次函数与一元一次不等式的关系
探究新知
任何一个一元一次不等式都可以转化为kx+b>0(或kx+b<0)的形式,所以解一元一次不等式kx+b>0(或kx+b<0),就是求使一次函数y=kx+b(k,b为常数,且k≠0)取正值(或负值)时x的取值范围.
知识归纳
一次函数与一元一次不等式的关系
例 画出函数 y=-3x+6 的图象,结合图象:
(1)求方程 -3x+6=0 的解;
O
x
y
y=-3x+6
A(0,6)
B(2,0)
解:函数 y=-3x+6 的图象如图所示,图象与x轴的交点是(2,0).
例题与练习
所以方程 -3x+6=0 的解就是交点B的横坐标:x=2.
O
x
y=-3x+6
A(0,6)
B(2,0)
解:结合图象可知,y>0时x的取值范围是 x<2; y<0时x的取值范围是 x>2.
所以,不等式-3x+6>0的解集是x<2,不等式-3x+6<0的解集是x>2.
(2)求不等式-3x+6>0和-3x+6<0的解集.
范例1
已知一次函数y=kx+b的图象如图所示,当x<-4时,y的取值范围是 ( )
A.y>0 B.y<0
C.-2
例题与练习
B
若函数y=ax+b(a≠0)的图象如图所示,则不等式
ax+b≥0的解集是( )
A.x≥3 B.x≤3 C.x=3 D.x≥
范例2
已知一次函数y=kx+b(k、b是常数,且k≠0),x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是 .
x -2 -1 0 1 2 3
y 3 2 1 0 -1 -2
x>1
仿例1
如图,直线y=kx+b分别交x轴和y轴于点A、B.
(1)关于x的方程kx+b=0的解是什么?
(2)当x为何值时,0
解:(1)x=-2;
(2)由图可知,
(3)把点(-2,0),(0,3)代入y=kx+b求得解析式为
y= x+3,
仿例2
当y= x+3>1时,x> .
当y>0时,x>-2;
当y<3时,x<0.∴-2
(1)求方程 3x-9=0 的解;
(2)求不等式 3x-9≤0 的解集;
(3)当 y=3 时,求x的值;
(4)当 y>3 时,求x的范围.
O
x
y
y=3x-9
A(0,-9)
B(3,0)
解:图象如图所示,
C(4,3)
(1)x=3;
练习
(3)x=4;
(2)x≤3;
(4)x>4.
随堂练习
1.一次函数y=-x+2的图象如图,你能说出-x+2<0的解集吗?
x
y
0
y=-x+2
2
解:x>2
2.一次函数y=kx+b的图象如图,你能说出kx+b<0的解集吗?
x
y
0
y=kx+b
-4
解:x < -4
3.利用图象解一元一次方程x+3=0.
解:作y=x+3图象如右图.
x
3
y=x+3
O
y
3
由图象知y=x+3交x轴于(-3,0),
所以原方程的解为x = 3 .
4.用画函数图象的方法解不等式5x+4<2x+10.
解:原不等式化为3x -6<0,
画出直线y = 3x -6(如图).
可以看出,当x<2 时这条直线上的点在x轴的下方,
即这时y = 3x -6 <0,
所以不等式的解集为x<2.
y=3x-6
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
即5x+4 <2x +10的解集为x<2.
解:画出两个函数
y=5x 1和y=2x+5的图象.
由图象知,两直线交于点 (2,9),所以原方程的解为 x=2.
O
y=5x 1
y=2x+5
9
2
x
y
5.利用函数图象求x的值:
5x 1= 2x+5.
课堂小结
一次函数与一元一次方程、一元一次不等式
解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式可以看作:当一次函数的函数值大(小)于0时,求自变量相应的取值范围.
