沪科版八年级数学上册12.4 综合实践 一次函数模型的应用 课件 (共17张PPT)
文档属性
| 名称 | 沪科版八年级数学上册12.4 综合实践 一次函数模型的应用 课件 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第十二章 一次函数
12.4 综合实践 一次函数模型的应用
导入新课
1.下列数据是弹簧挂重物后的长度记录,测出弹簧长度y与重物质量x之间的函数关系式为 ,挂重30千克时,弹簧长度为 .
重物质量/kg 0 1 2 3 4 … 30 …
弹簧长度/cm 12 12.5 13 13.5 14 … …
2.如何从表格中观察出两个变量间是否为一次函数?
答:每两个相邻的函数值的差与对应两个自变量值的差比值总相等,即可判定为一次函数.
y=0.5x+12
27cm
探究新知
一次函数模型的应用
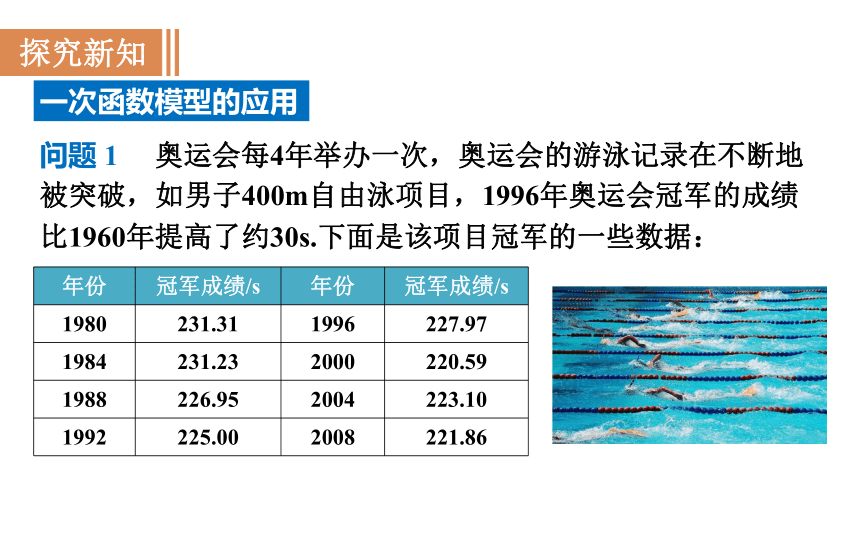
问题 1 奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400m自由泳项目,1996年奥运会冠军的成绩比1960年提高了约30s.下面是该项目冠军的一些数据:
年份 冠军成绩/s 年份 冠军成绩/s
1980 231.31 1996 227.97
1984 231.23 2000 220.59
1988 226.95 2004 223.10
1992 225.00 2008 221.86
根据上面资料,能否估计2012年伦敦奥运会时该项目的冠军成绩?
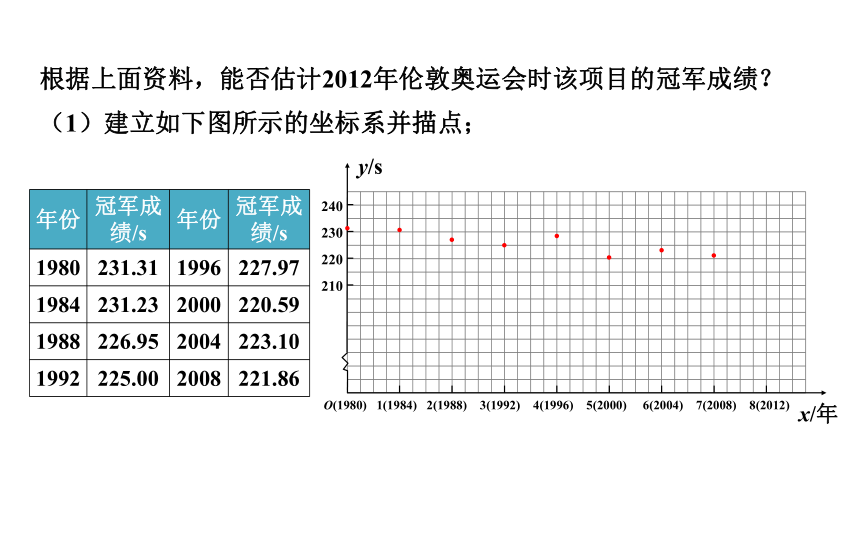
(1)建立如下图所示的坐标系并描点;
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
年份 冠军成绩/s 年份 冠军成绩/s
1980 231.31 1996 227.97
1984 231.23 2000 220.59
1988 226.95 2004 223.10
1992 225.00 2008 221.86
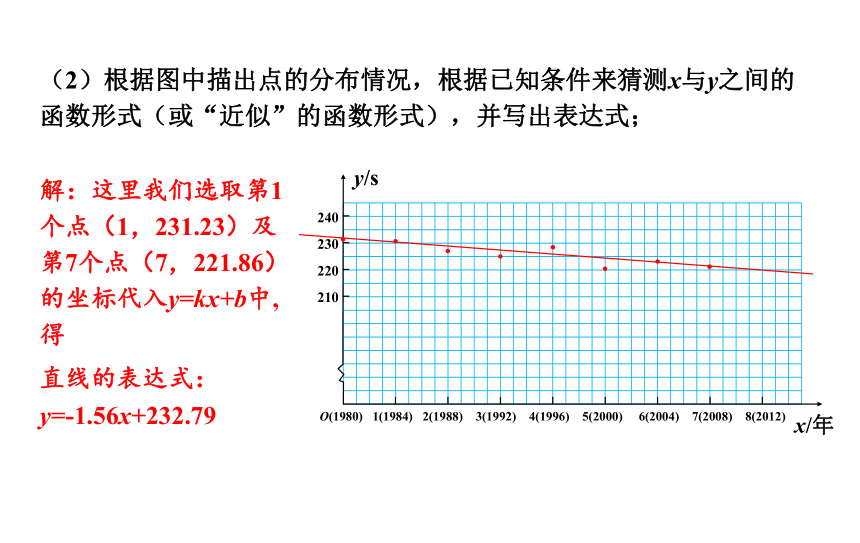
(2)根据图中描出点的分布情况,根据已知条件来猜测x与y之间的函数形式(或“近似”的函数形式),并写出表达式;
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
解:这里我们选取第1个点(1,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得
直线的表达式:
y=-1.56x+232.79
(3)根据你建立的模型,估计2012年伦敦奥运会该项目的冠军成绩;
解:直线的表达式:y=-1.56x+232.79
当x=8时,y=220.31
2012年伦敦奥运会中国选手孙杨以220.14s成为冠军.
220.31s接近220.14s.
(4)能否用上述模型预测2016年里约热内卢奥运会该项目的冠军成绩?
知识归纳
通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:
(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题.
范例
例题与练习
已知部分鞋子的型号“码”数与鞋子长度“cm”之间存在一种换算关系如下:
尺寸/cm 15 20 25
型号/码 20 30 40
(1)通过画图、观察,猜想这种换算规律可能用哪种函数关系去模拟;
(2)设鞋子的长度为xcm,“码”数为y,试写出y与x之间的函数表达式;
(3)小刚平时穿39码的鞋子,那么他鞋长多少厘米?
(4)据说篮球巨人姚明的鞋长31cm,那么他穿多大码的鞋?
(2)设y=kx+b(k≠0),代入x=15,y=20;
x=20,y=30,可求得函数解析式为y=2x-10;
(4)52码.
(3)24.5cm;
解:(1)一次函数,
∵ =2, =2,可知其为一次函数关系;
尺寸/cm 15 20 25
型号/码 20 30 40
问题情境:用同样大小的黑色棋子按如图所示的规律摆放,则第2015个图形共有多少枚棋子?
仿例1
解:以图形的序号为横坐标,棋子的枚数为纵坐标,
描点:(1,4)、(2,7)、(3,10)、(4,13),
依次连接以上各点,所有的点在一条直线上.
设直线解析式为y=kx+b,
把(1,4)、(2,7)两点坐标代入得
所以y=3x+1.
验证:当x=3时,y=10.
所以,另外一点也在这条直线上.
当x=2015时,y=3×2015+1=6046.
即第2015个图形有6046枚棋子.
解得
o
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
y
8
9
x
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x(元) 15 20 25 30 35 …
y(件) 25 20 15 10 5 …
(1)在直角坐标系中描出相应的点;
(2)猜测y(件)与x(元)之间的函数关系;
(3)当销售价定为28元时,求每日的销售利润.
解:(1)描点画图,如图所示;
仿例2
o
10
20
30
40
50
60
70
10
20
30
40
50
y(件)
x(元)
(2)由图象猜测y与x之间的函数关系为一次函数关系.
∴一次函数解析式为y=-x+40,将其余各点代入验证均适合.
则 解得
o
10
20
30
40
50
60
70
10
20
30
40
50
y(件)
x(元)
设一次函数解析式为y=kx+b,
所以,所求一次函数的解析式为y=-x+40;
(3)当x=28时,y=-28+40=12.
∴所获销售利润为(28-10)×12=216(元).
销售价定为28元时,每日的销售利润是216元.
随堂练习
1.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(。F)计量法.两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/。F 32 50 68 86 104 122
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;
o
10
20
30
40
50
60
70
20
40
60
80
100
y( 。F )
x(。 C)
120
(2)确定y与x之间的函数表达式,并加以检验;
解:设y=kx+b,把(0,32)和(10,50)代入得
解得
经检验,点(20,68),(30,86),(40,104),(50,122)的坐标均能满足上述表达式,所以y与x之间的函数表达式为
o
10
20
30
40
50
60
70
20
40
60
80
100
y( 。F )
x(。 C)
120
(3)华氏0度时的温度应是多少摄氏度?
解:当y=0时,
解得
∴华氏0度时的温度应是 摄氏度;
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
∴ 华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
解:把y=x代入,
解得
课堂小结
一次函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
第十二章 一次函数
12.4 综合实践 一次函数模型的应用
导入新课
1.下列数据是弹簧挂重物后的长度记录,测出弹簧长度y与重物质量x之间的函数关系式为 ,挂重30千克时,弹簧长度为 .
重物质量/kg 0 1 2 3 4 … 30 …
弹簧长度/cm 12 12.5 13 13.5 14 … …
2.如何从表格中观察出两个变量间是否为一次函数?
答:每两个相邻的函数值的差与对应两个自变量值的差比值总相等,即可判定为一次函数.
y=0.5x+12
27cm
探究新知
一次函数模型的应用
问题 1 奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400m自由泳项目,1996年奥运会冠军的成绩比1960年提高了约30s.下面是该项目冠军的一些数据:
年份 冠军成绩/s 年份 冠军成绩/s
1980 231.31 1996 227.97
1984 231.23 2000 220.59
1988 226.95 2004 223.10
1992 225.00 2008 221.86
根据上面资料,能否估计2012年伦敦奥运会时该项目的冠军成绩?
(1)建立如下图所示的坐标系并描点;
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
年份 冠军成绩/s 年份 冠军成绩/s
1980 231.31 1996 227.97
1984 231.23 2000 220.59
1988 226.95 2004 223.10
1992 225.00 2008 221.86
(2)根据图中描出点的分布情况,根据已知条件来猜测x与y之间的函数形式(或“近似”的函数形式),并写出表达式;
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
解:这里我们选取第1个点(1,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得
直线的表达式:
y=-1.56x+232.79
(3)根据你建立的模型,估计2012年伦敦奥运会该项目的冠军成绩;
解:直线的表达式:y=-1.56x+232.79
当x=8时,y=220.31
2012年伦敦奥运会中国选手孙杨以220.14s成为冠军.
220.31s接近220.14s.
(4)能否用上述模型预测2016年里约热内卢奥运会该项目的冠军成绩?
知识归纳
通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:
(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题.
范例
例题与练习
已知部分鞋子的型号“码”数与鞋子长度“cm”之间存在一种换算关系如下:
尺寸/cm 15 20 25
型号/码 20 30 40
(1)通过画图、观察,猜想这种换算规律可能用哪种函数关系去模拟;
(2)设鞋子的长度为xcm,“码”数为y,试写出y与x之间的函数表达式;
(3)小刚平时穿39码的鞋子,那么他鞋长多少厘米?
(4)据说篮球巨人姚明的鞋长31cm,那么他穿多大码的鞋?
(2)设y=kx+b(k≠0),代入x=15,y=20;
x=20,y=30,可求得函数解析式为y=2x-10;
(4)52码.
(3)24.5cm;
解:(1)一次函数,
∵ =2, =2,可知其为一次函数关系;
尺寸/cm 15 20 25
型号/码 20 30 40
问题情境:用同样大小的黑色棋子按如图所示的规律摆放,则第2015个图形共有多少枚棋子?
仿例1
解:以图形的序号为横坐标,棋子的枚数为纵坐标,
描点:(1,4)、(2,7)、(3,10)、(4,13),
依次连接以上各点,所有的点在一条直线上.
设直线解析式为y=kx+b,
把(1,4)、(2,7)两点坐标代入得
所以y=3x+1.
验证:当x=3时,y=10.
所以,另外一点也在这条直线上.
当x=2015时,y=3×2015+1=6046.
即第2015个图形有6046枚棋子.
解得
o
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
y
8
9
x
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x(元) 15 20 25 30 35 …
y(件) 25 20 15 10 5 …
(1)在直角坐标系中描出相应的点;
(2)猜测y(件)与x(元)之间的函数关系;
(3)当销售价定为28元时,求每日的销售利润.
解:(1)描点画图,如图所示;
仿例2
o
10
20
30
40
50
60
70
10
20
30
40
50
y(件)
x(元)
(2)由图象猜测y与x之间的函数关系为一次函数关系.
∴一次函数解析式为y=-x+40,将其余各点代入验证均适合.
则 解得
o
10
20
30
40
50
60
70
10
20
30
40
50
y(件)
x(元)
设一次函数解析式为y=kx+b,
所以,所求一次函数的解析式为y=-x+40;
(3)当x=28时,y=-28+40=12.
∴所获销售利润为(28-10)×12=216(元).
销售价定为28元时,每日的销售利润是216元.
随堂练习
1.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(。F)计量法.两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/。F 32 50 68 86 104 122
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;
o
10
20
30
40
50
60
70
20
40
60
80
100
y( 。F )
x(。 C)
120
(2)确定y与x之间的函数表达式,并加以检验;
解:设y=kx+b,把(0,32)和(10,50)代入得
解得
经检验,点(20,68),(30,86),(40,104),(50,122)的坐标均能满足上述表达式,所以y与x之间的函数表达式为
o
10
20
30
40
50
60
70
20
40
60
80
100
y( 。F )
x(。 C)
120
(3)华氏0度时的温度应是多少摄氏度?
解:当y=0时,
解得
∴华氏0度时的温度应是 摄氏度;
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
∴ 华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
解:把y=x代入,
解得
课堂小结
一次函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
