沪科版八年级数学上册13.1.2 三角形中角的关系 课件 (共16张PPT)
文档属性
| 名称 | 沪科版八年级数学上册13.1.2 三角形中角的关系 课件 (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 772.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 11:35:58 | ||
图片预览


文档简介
(共16张PPT)
13.1.2 三角形中角的关系
第十三章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
导入新课
答:由不在同一直线上的三条线段首尾顺次相接所组成的封闭图形叫三角形.
等腰三角形(等边三角形是它的特例)
不等边三角形
三角形
1.什么是三角形?三角形按边如何分类?
2.三角形三边关系是什么?
答:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.
旧知回顾
探究新知
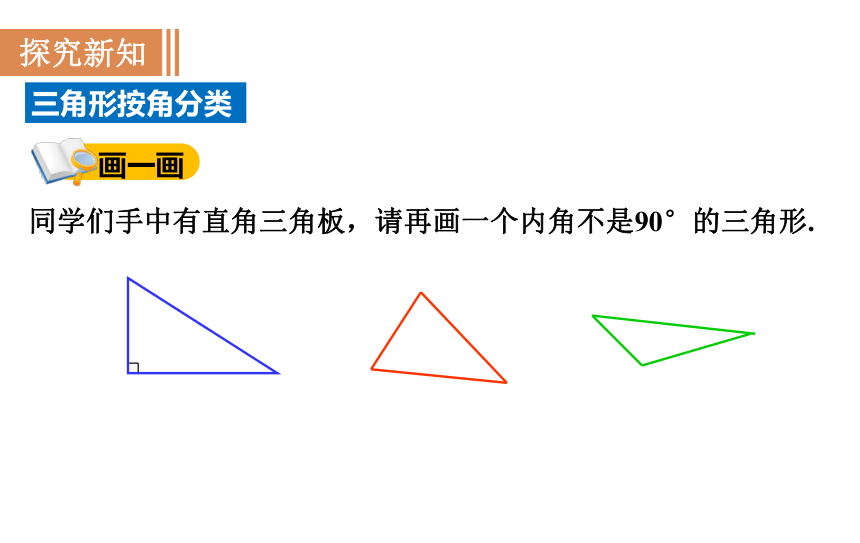
三角形按角分类
画一画
同学们手中有直角三角板,请再画一个内角不是90°的三角形.
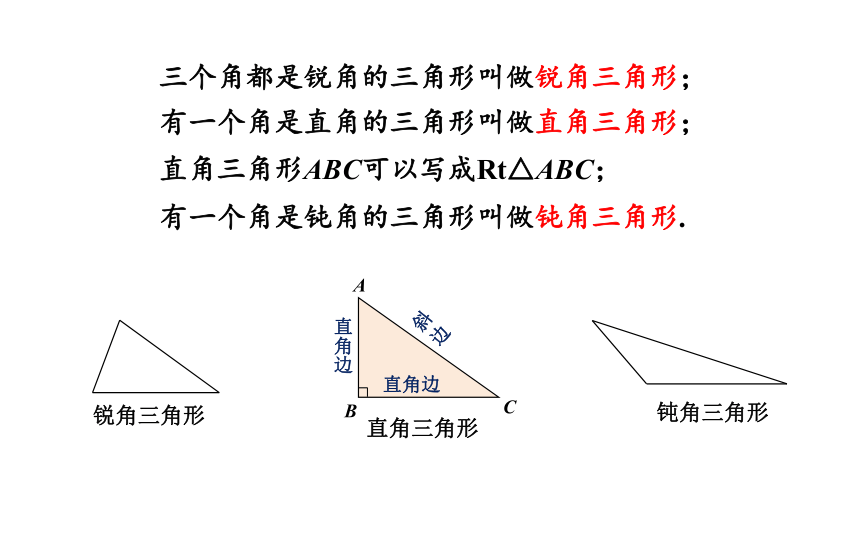
三个角都是锐角的三角形叫做锐角三角形;
锐角三角形
有一个角是钝角的三角形叫做钝角三角形.
钝角三角形
有一个角是直角的三角形叫做直角三角形;
直角三角形
直角边
直角边
斜边
A
B
C
直角三角形ABC可以写成Rt△ABC;
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形
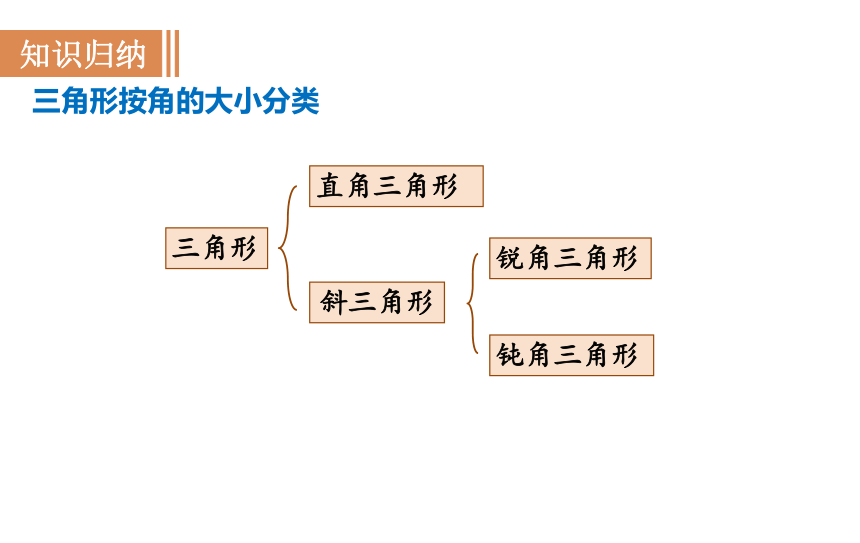
三角形按角的大小分类
知识归纳
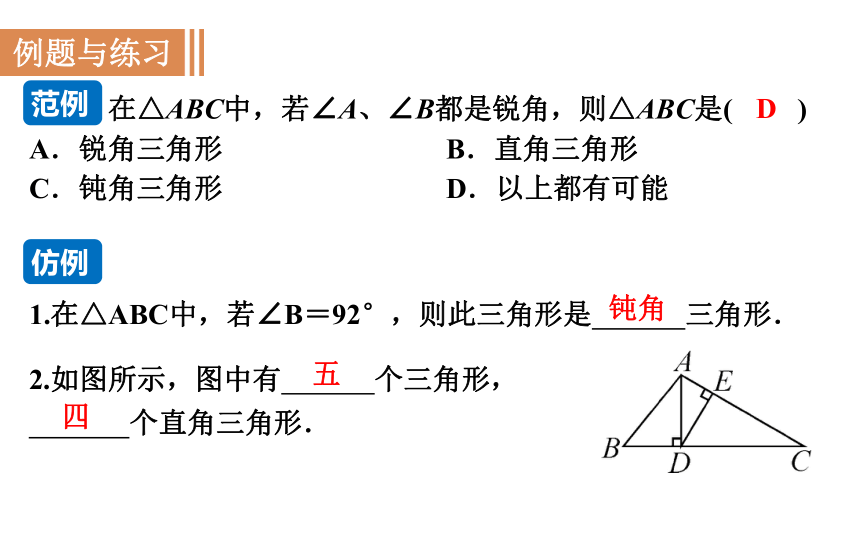
在△ABC中,若∠A、∠B都是锐角,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
D
范例
例题与练习
仿例
1.在△ABC中,若∠B=92°,则此三角形是 三角形.
钝角
2.如图所示,图中有 个三角形,
个直角三角形.
五
四
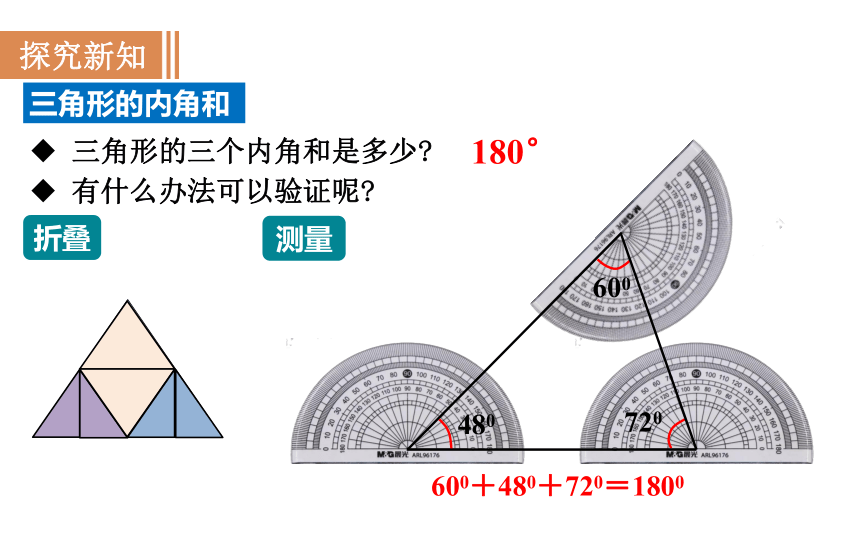
三角形的内角和
三角形的三个内角和是多少
有什么办法可以验证呢
探究新知
折叠
180°
480
720
600
600+480+720=1800
测量
A
B
C
1
2
3
E
F
剪拼
例题与练习
例
A
B
C
D
解:因为 BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,∠A+ ∠ABD+ ∠ADB=180 °, (三角形的内角和等于180°)
∠A=180°-∠ABD-∠ADB=180°-54°-90°=36°.
已知:在△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A和∠C的度数.
∠ABD=54°, ∠ADB=90°,(已知)
在△ABC中,
∠C=180°-∠A-(∠ABD+∠DBC)=180°-36°-(54°+18°)
=72°.
典例
如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是
( )
A.46° B.66° C.54° D.80°
C
仿例
如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为( )
A.17° B.34° C.56° D.124°
C
变例
如图所示,∠B=42°,∠A+10°=∠1,∠ACD=64°,试说明AB∥CD.
证明:∵∠A+∠1+∠B=180°,
又∵∠B=42°,∠1=∠A+40°,
∴42°+∠A+∠A+10°=180°,
∴∠A=64°,
∴∠A=∠ACD,
∴AB∥CD.
随堂练习
1. 在△ABC中:
(1)已知:∠A=105°,∠B-∠C= 15°,则∠C= ;
(2)已知:∠A:∠B:∠C=3:4:5,则∠C= ;
30°
75°
2. 已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°.求∠CAD的度数.
A
B
C
D
解:∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=180°-90°-70°=20°,
又∵∠BAC=46°,
∴∠CAD=46°-20°=26°
3.如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,
∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°-∠CFD-∠FCD=40°.
课堂小结
三角形中角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于180°
锐角三角形
钝角三角形
13.1.2 三角形中角的关系
第十三章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
导入新课
答:由不在同一直线上的三条线段首尾顺次相接所组成的封闭图形叫三角形.
等腰三角形(等边三角形是它的特例)
不等边三角形
三角形
1.什么是三角形?三角形按边如何分类?
2.三角形三边关系是什么?
答:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.
旧知回顾
探究新知
三角形按角分类
画一画
同学们手中有直角三角板,请再画一个内角不是90°的三角形.
三个角都是锐角的三角形叫做锐角三角形;
锐角三角形
有一个角是钝角的三角形叫做钝角三角形.
钝角三角形
有一个角是直角的三角形叫做直角三角形;
直角三角形
直角边
直角边
斜边
A
B
C
直角三角形ABC可以写成Rt△ABC;
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形
三角形按角的大小分类
知识归纳
在△ABC中,若∠A、∠B都是锐角,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
D
范例
例题与练习
仿例
1.在△ABC中,若∠B=92°,则此三角形是 三角形.
钝角
2.如图所示,图中有 个三角形,
个直角三角形.
五
四
三角形的内角和
三角形的三个内角和是多少
有什么办法可以验证呢
探究新知
折叠
180°
480
720
600
600+480+720=1800
测量
A
B
C
1
2
3
E
F
剪拼
例题与练习
例
A
B
C
D
解:因为 BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,∠A+ ∠ABD+ ∠ADB=180 °, (三角形的内角和等于180°)
∠A=180°-∠ABD-∠ADB=180°-54°-90°=36°.
已知:在△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A和∠C的度数.
∠ABD=54°, ∠ADB=90°,(已知)
在△ABC中,
∠C=180°-∠A-(∠ABD+∠DBC)=180°-36°-(54°+18°)
=72°.
典例
如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是
( )
A.46° B.66° C.54° D.80°
C
仿例
如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为( )
A.17° B.34° C.56° D.124°
C
变例
如图所示,∠B=42°,∠A+10°=∠1,∠ACD=64°,试说明AB∥CD.
证明:∵∠A+∠1+∠B=180°,
又∵∠B=42°,∠1=∠A+40°,
∴42°+∠A+∠A+10°=180°,
∴∠A=64°,
∴∠A=∠ACD,
∴AB∥CD.
随堂练习
1. 在△ABC中:
(1)已知:∠A=105°,∠B-∠C= 15°,则∠C= ;
(2)已知:∠A:∠B:∠C=3:4:5,则∠C= ;
30°
75°
2. 已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°.求∠CAD的度数.
A
B
C
D
解:∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=180°-90°-70°=20°,
又∵∠BAC=46°,
∴∠CAD=46°-20°=26°
3.如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,
∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°-∠CFD-∠FCD=40°.
课堂小结
三角形中角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于180°
锐角三角形
钝角三角形
