沪科版八年级数学上册13.1.3 三角形中几条重要线段 课件 (共21张PPT)
文档属性
| 名称 | 沪科版八年级数学上册13.1.3 三角形中几条重要线段 课件 (共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
第十三章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
13.1.3 三角形中几条重要线段
旧知回顾
导入新课
1.三角形按角如何分类?
答:三角形内角和为180°.
答:分为锐角三角形、直角三角形、钝角三角形.
2.三角形内角和是什么?
3.如图过P点向AB作垂线段,垂点在线段AB上吗?
解:作图如图,
A
B
P
垂足不在AB上,在BA的延长线上.
探究新知
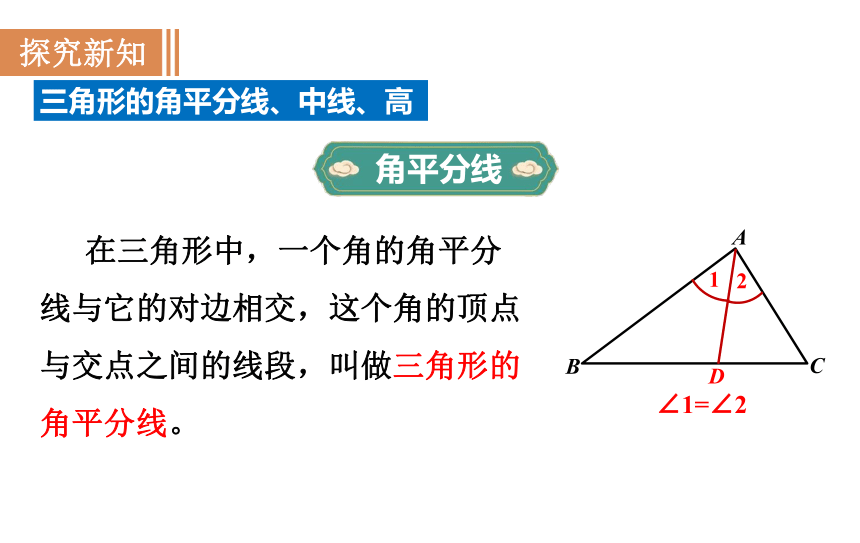
在三角形中,一个角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
B
A
C
D
∠1=∠2
1
2
三角形的角平分线、中线、高
角平分线
B
A
C
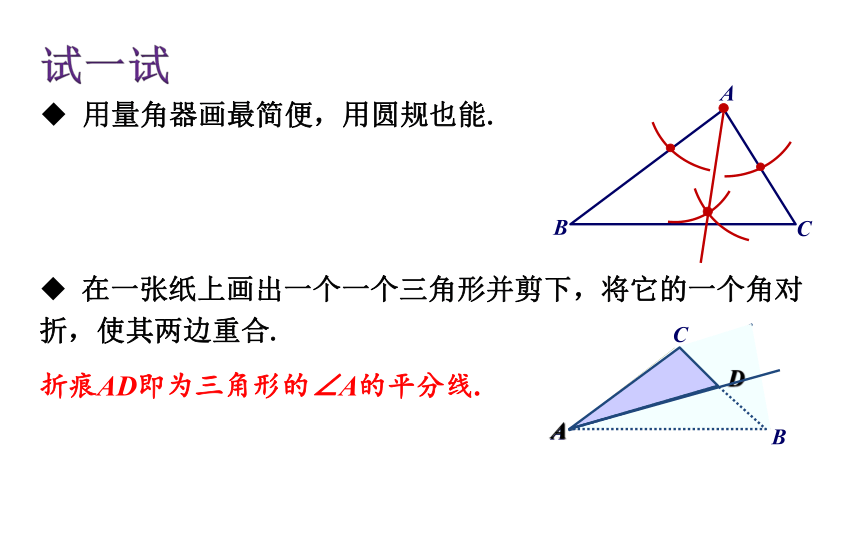
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
试一试
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线。
A
BE=EC
B
C
E
如图,右图AE是BC边上的中线
中 线
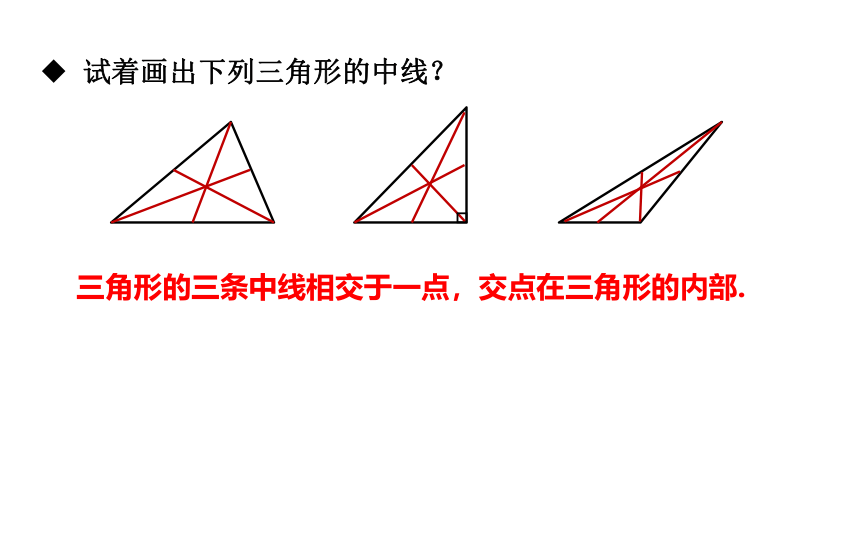
试着画出下列三角形的中线?
三角形的三条中线相交于一点,交点在三角形的内部.
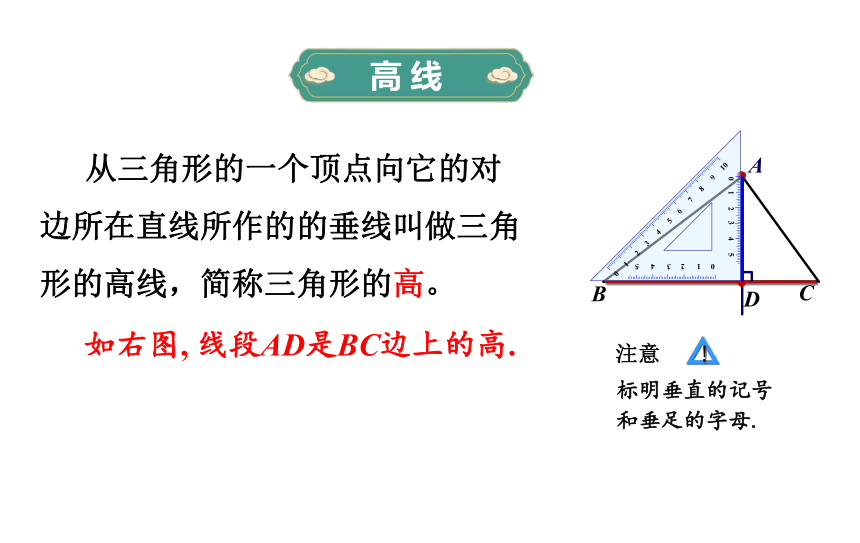
从三角形的一个顶点向它的对边所在直线所作的的垂线叫做三角形的高线,简称三角形的高。
A
B
C
D
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
高 线
如右图, 线段AD是BC边上的高.
和垂足的字母.
注意
!
标明垂直的记号
操作
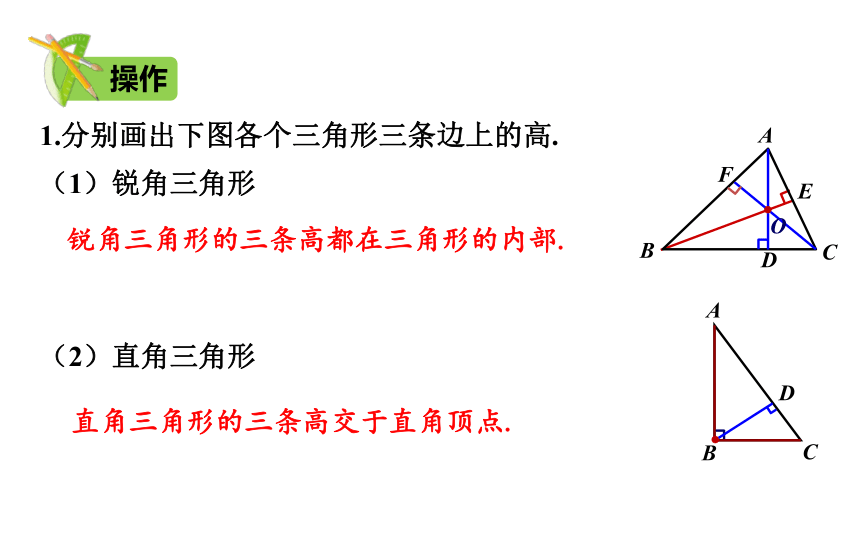
1.分别画出下图各个三角形三条边上的高.
O
(1)锐角三角形
锐角三角形的三条高都在三角形的内部.
(2)直角三角形
A
B
C
D
直角三角形的三条高交于直角顶点.
A
B
C
D
E
F
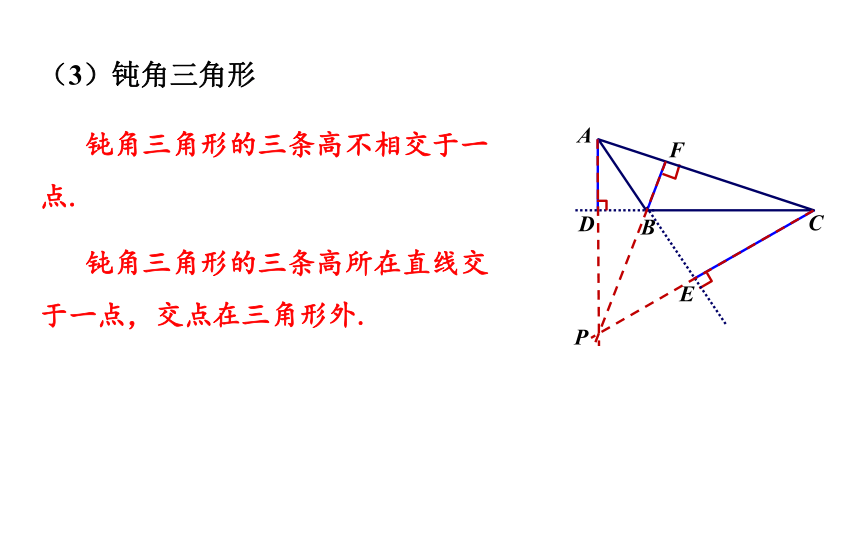
(3)钝角三角形
A
B
C
D
F
E
钝角三角形的三条高不相交于一点.
P
钝角三角形的三条高所在直线交于一点,交点在三角形外.
2.任意画一个三角形,画出三边上的中线.
o
三角形,三条中线交于一点,这个交点就是三角形的重心.
知识归纳
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
范例
例题与练习
不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.三角形的中位线
C
仿例
小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )
C
三角形中有关角平分线、中线、和高的常见计算
如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35cm,BC=11cm,且△ABD与△ACD的周长差为3cm,求AB与AC的长.
A
C
D
B
解: ∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
又∵△ABD与△ACD的周长差为3cm,
∴AB-AC=3cm,
∴AB=13.5cm,AC=10.5cm.
例
如图,△ABC中,∠B=40°,∠C=60°,AD⊥BC,AE平分∠BAC,求∠1的度数.
典例
解:在△ABC中,∠B=40°,∠C=60°,
又∵在△ADC中,∠ADC=90°,∠C=60°,
∴∠EAC= ∠BAC= ×80°=40°
∴∠DAC=30°,
∴∠1=∠EAC-∠DAC=40°-30°=10°.
∴∠BAC =180°- ∠B- ∠C
= 180°- 40°- 60°= 80°
∵AE平分∠BAC,
仿例
A
如图,已知BD是△ABC的中线,AB=5,
BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3
C.6 D.不能确定
如图,在△ABC中,CD是△ABC的角平分线,DE∥BC,交AC于点E,若∠ACB=60°,则∠EDC= .
30°
随堂练习
填空:
(1)如果AD是△ABC的高,那么∠BDA= ;
(2)如果BE是△ABC的角平分线,那么∠ABE=∠ =
∠ ;
(3)如果CM是△ABC的中线,那么△ACM的面积_______
△BCM的面积(填“<”“>”或“=”).
90°
EBC
ABC
=
2.如图△ABC中,AB=AC,画出底边BC上的中线、高和顶角∠A的平分线,你发现这三条线段有什么关系?
A
B
C
BD=CD
AD⊥BC
∠BAD=∠CAD
等腰三角形底边上的中线、高和顶角的平分线,三条线段重合.
D
3.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
4.如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
∴∠BAE=37.5°.
课堂小结
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
定义
第十三章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
13.1.3 三角形中几条重要线段
旧知回顾
导入新课
1.三角形按角如何分类?
答:三角形内角和为180°.
答:分为锐角三角形、直角三角形、钝角三角形.
2.三角形内角和是什么?
3.如图过P点向AB作垂线段,垂点在线段AB上吗?
解:作图如图,
A
B
P
垂足不在AB上,在BA的延长线上.
探究新知
在三角形中,一个角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
B
A
C
D
∠1=∠2
1
2
三角形的角平分线、中线、高
角平分线
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
试一试
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线。
A
BE=EC
B
C
E
如图,右图AE是BC边上的中线
中 线
试着画出下列三角形的中线?
三角形的三条中线相交于一点,交点在三角形的内部.
从三角形的一个顶点向它的对边所在直线所作的的垂线叫做三角形的高线,简称三角形的高。
A
B
C
D
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
高 线
如右图, 线段AD是BC边上的高.
和垂足的字母.
注意
!
标明垂直的记号
操作
1.分别画出下图各个三角形三条边上的高.
O
(1)锐角三角形
锐角三角形的三条高都在三角形的内部.
(2)直角三角形
A
B
C
D
直角三角形的三条高交于直角顶点.
A
B
C
D
E
F
(3)钝角三角形
A
B
C
D
F
E
钝角三角形的三条高不相交于一点.
P
钝角三角形的三条高所在直线交于一点,交点在三角形外.
2.任意画一个三角形,画出三边上的中线.
o
三角形,三条中线交于一点,这个交点就是三角形的重心.
知识归纳
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
范例
例题与练习
不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.三角形的中位线
C
仿例
小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )
C
三角形中有关角平分线、中线、和高的常见计算
如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35cm,BC=11cm,且△ABD与△ACD的周长差为3cm,求AB与AC的长.
A
C
D
B
解: ∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
又∵△ABD与△ACD的周长差为3cm,
∴AB-AC=3cm,
∴AB=13.5cm,AC=10.5cm.
例
如图,△ABC中,∠B=40°,∠C=60°,AD⊥BC,AE平分∠BAC,求∠1的度数.
典例
解:在△ABC中,∠B=40°,∠C=60°,
又∵在△ADC中,∠ADC=90°,∠C=60°,
∴∠EAC= ∠BAC= ×80°=40°
∴∠DAC=30°,
∴∠1=∠EAC-∠DAC=40°-30°=10°.
∴∠BAC =180°- ∠B- ∠C
= 180°- 40°- 60°= 80°
∵AE平分∠BAC,
仿例
A
如图,已知BD是△ABC的中线,AB=5,
BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3
C.6 D.不能确定
如图,在△ABC中,CD是△ABC的角平分线,DE∥BC,交AC于点E,若∠ACB=60°,则∠EDC= .
30°
随堂练习
填空:
(1)如果AD是△ABC的高,那么∠BDA= ;
(2)如果BE是△ABC的角平分线,那么∠ABE=∠ =
∠ ;
(3)如果CM是△ABC的中线,那么△ACM的面积_______
△BCM的面积(填“<”“>”或“=”).
90°
EBC
ABC
=
2.如图△ABC中,AB=AC,画出底边BC上的中线、高和顶角∠A的平分线,你发现这三条线段有什么关系?
A
B
C
BD=CD
AD⊥BC
∠BAD=∠CAD
等腰三角形底边上的中线、高和顶角的平分线,三条线段重合.
D
3.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
4.如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
∴∠BAE=37.5°.
课堂小结
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
定义
