沪科版八年级数学上册 13.2.2 定理与证明 课件(共18张PPT)
文档属性
| 名称 | 沪科版八年级数学上册 13.2.2 定理与证明 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 485.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.2 定理与证明
旧知回顾
导入新课
答:对某一事件作出正确或不正确判断的语句叫做命题.
1.什么是命题?命题结构是怎样的?什么是真命题?什么是假命题?
命题通常由题设和结论两部分组成.
正确的命题叫真命题.
错误的命题叫假命题.
2.什么叫互逆命题?什么是原命题和逆命题?
答:把一个命题的题设和结论互换得到一个新命题,这两个命题叫互逆命题
其中一个命题叫原命题,另一个是原命题的逆命题.
探究新知
总结:有些命题,如:“对顶角相等”,“三角形三个内角的和等于180°”等,它们的正确性已经经过推理得到证实,并被作为判断其他命题真假的依据,这样的真命题称为定理。
做一做:下列命题中,哪些正确,哪些错误?
(1)每一个月都有31天;
(2)如果a是有理数,那么a是整数;
(3)同位角相等;
(4)同角的补角相等.
错误
错误
错误
正确
你能说说你是怎么判断的吗?
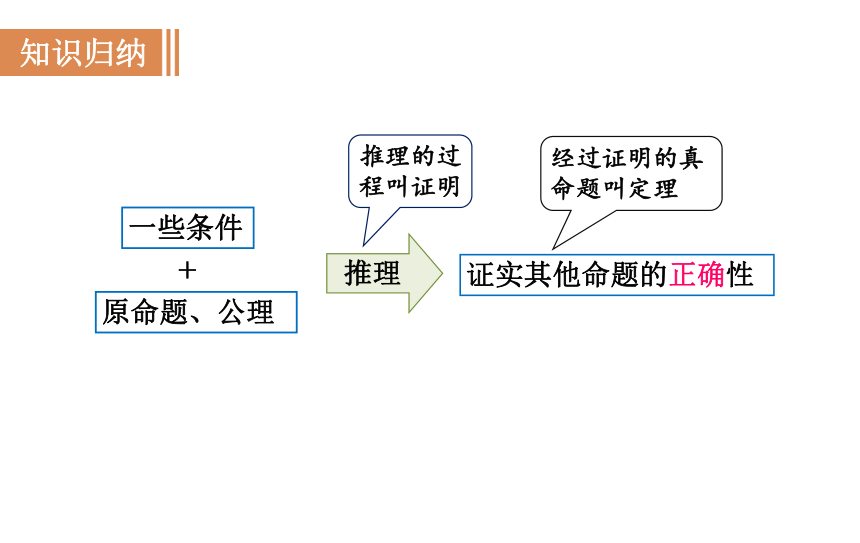
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
原命题、公理
一些条件
+
知识归纳
范例
1:“同角或等角的补角相等”是( )
A.定义 B.题设
C.定理 D.假命题
C
2.下列四个命题:①内错角相等,两直线平行;②有两条边相等的三角形叫做等腰三角形;③过两点有且只有一条直线;④经过直线外一点有且只有一条直线与已知直线平行,其中是定理的是 (填序号).
①
例题与练习
1.下列说法中错误的是 ( )
A.所有的命题都是定理
B.定理是真命题
C.公理是真命题
D.“画线段AB=CD”不是命题
A
2.“两条直线相交成直角,就叫两直线互相垂直”这个句子是 ( )
A.定义 B.假命题 C.公理 D.定理
A
仿例
证明与推理
从已知条件出发,根据定义、基本事实、已证定理,并按照逻辑规则,推导出结论的方法叫“演绎推理”。
推理的过程叫做证明.
例1
例题与练习
已知:如图,直线c与直线a、b相交,且 ∠1=∠2.
求证:a∥b.
a
b
c
3
1
2
证明:
∵ ∠1=∠2, (已知)
又∵ ∠1=∠3,(对顶角相等)
∴∠2=∠3, (等量代换)
∴ a∥b, (同位角相等,两直线平行)
证明: ∵ OE平分∠AOB,
OF平分∠BOC,
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB, OF平分∠BOC.求证:OE⊥OF.
A
O
C
E
B
F
1
2
例2
∴∠1= ∠AOB,∠2= ∠BOC.
又∵∠AOB、∠BOC互为邻补角,
∴∠AOB+∠BOC=180°,
∴∠1+∠2= (∠AOB+∠BOC)=90°,
∴OE⊥OF.
范例
下列推理中,错误的是 ( )
A.∵AB=CD,CD=EF,∴AB=EF
B.∵∠α=∠β,∠β=∠r,∴∠α=∠r
C.∵a∥b,b∥c,∴a∥c
D.∵AB⊥EF,EF⊥CD,∴AB⊥CD
D
仿例
如图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.求证:AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(_____),
∴AD∥EF( ),
∴ = (两直线平行,内错角相等),
∠2=∠3( ).
∵∠1=∠2( ),∴ = ( ),
∴AD平分∠BAC( ).
已知
垂直于同一直线的两直线平行
∠1
∠4
两直线平行,同位角相等
已知
∠3
∠4
角平分线定义
等量代换
随堂练习
1.在下列各题的括号内,填上推理的依据:
(1)已知:如图,点B、A、E在一条直线上,∠1=∠B.
求证:∠2=∠C.
A
B
C
D
E
1
2
证明 ∵∠1=∠B( )
∴AD∥BC( )
∴∠2=∠C( )
已知
同位角相等,两直线平行
两直线平行,内错角相等
(2)已知,如图,∠1=∠2.求证:AB∥CD
A
B
C
D
E
F
1
2
3
证明 ∵∠1=∠2( )
又∵∠2∥∠3( )
∴∠1=∠3( )
∴AB//CD( )
已知
对顶角相等
等量代换
同位角相等,两直线平行
A
B
C
D
E
F
1
2
2.已知:如图,DC//AB,DF平分∠CDB,BE平分∠ABD.
求证:∠1 = ∠2.
证明 ∵DC//AB(已知 )
∴∠ABD=∠CDB.
(两直线平行,内错角相等)
又 ∵DF平分∠CDB,(已知)
BE平分∠ABD,(已知)
∴∠1=∠2.(等量代换)
∴∠1= ∠CDB,(角平分线的定义)
∠2= ∠ABD. (角平分线的定义)
3.已知:如图,直线AB与直线CD相交于点O,∠AOC与∠BOD是对顶角.求证:∠AOC =∠BOD.
证明:
∴ ∠AOB与∠COD都是平角(平角的定义 ),
∴ ∠AOC+∠AOD=180°,
∴ ∠AOC =∠BOD (同角的补角相等 ).
∵直线AB与直线CD相交于点O,
∠BOD+∠AOD=180°,
4.已知,如图:∠1=∠B,求证:∠2=∠C.
A
B
C
D
E
1
2
证明:∵∠1=∠B(已知),
∴AE∥BC(同位角相等,两直线平行),
∴∠2=∠(两直线平行,内错角相等).
课堂小结
证明
定理:经过证明的真命题称为定理.
证明:除了公理外,其他真命题的正确性都通过推理的方法证实.推理的过程称为证明.
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.2 定理与证明
旧知回顾
导入新课
答:对某一事件作出正确或不正确判断的语句叫做命题.
1.什么是命题?命题结构是怎样的?什么是真命题?什么是假命题?
命题通常由题设和结论两部分组成.
正确的命题叫真命题.
错误的命题叫假命题.
2.什么叫互逆命题?什么是原命题和逆命题?
答:把一个命题的题设和结论互换得到一个新命题,这两个命题叫互逆命题
其中一个命题叫原命题,另一个是原命题的逆命题.
探究新知
总结:有些命题,如:“对顶角相等”,“三角形三个内角的和等于180°”等,它们的正确性已经经过推理得到证实,并被作为判断其他命题真假的依据,这样的真命题称为定理。
做一做:下列命题中,哪些正确,哪些错误?
(1)每一个月都有31天;
(2)如果a是有理数,那么a是整数;
(3)同位角相等;
(4)同角的补角相等.
错误
错误
错误
正确
你能说说你是怎么判断的吗?
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
原命题、公理
一些条件
+
知识归纳
范例
1:“同角或等角的补角相等”是( )
A.定义 B.题设
C.定理 D.假命题
C
2.下列四个命题:①内错角相等,两直线平行;②有两条边相等的三角形叫做等腰三角形;③过两点有且只有一条直线;④经过直线外一点有且只有一条直线与已知直线平行,其中是定理的是 (填序号).
①
例题与练习
1.下列说法中错误的是 ( )
A.所有的命题都是定理
B.定理是真命题
C.公理是真命题
D.“画线段AB=CD”不是命题
A
2.“两条直线相交成直角,就叫两直线互相垂直”这个句子是 ( )
A.定义 B.假命题 C.公理 D.定理
A
仿例
证明与推理
从已知条件出发,根据定义、基本事实、已证定理,并按照逻辑规则,推导出结论的方法叫“演绎推理”。
推理的过程叫做证明.
例1
例题与练习
已知:如图,直线c与直线a、b相交,且 ∠1=∠2.
求证:a∥b.
a
b
c
3
1
2
证明:
∵ ∠1=∠2, (已知)
又∵ ∠1=∠3,(对顶角相等)
∴∠2=∠3, (等量代换)
∴ a∥b, (同位角相等,两直线平行)
证明: ∵ OE平分∠AOB,
OF平分∠BOC,
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB, OF平分∠BOC.求证:OE⊥OF.
A
O
C
E
B
F
1
2
例2
∴∠1= ∠AOB,∠2= ∠BOC.
又∵∠AOB、∠BOC互为邻补角,
∴∠AOB+∠BOC=180°,
∴∠1+∠2= (∠AOB+∠BOC)=90°,
∴OE⊥OF.
范例
下列推理中,错误的是 ( )
A.∵AB=CD,CD=EF,∴AB=EF
B.∵∠α=∠β,∠β=∠r,∴∠α=∠r
C.∵a∥b,b∥c,∴a∥c
D.∵AB⊥EF,EF⊥CD,∴AB⊥CD
D
仿例
如图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.求证:AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(_____),
∴AD∥EF( ),
∴ = (两直线平行,内错角相等),
∠2=∠3( ).
∵∠1=∠2( ),∴ = ( ),
∴AD平分∠BAC( ).
已知
垂直于同一直线的两直线平行
∠1
∠4
两直线平行,同位角相等
已知
∠3
∠4
角平分线定义
等量代换
随堂练习
1.在下列各题的括号内,填上推理的依据:
(1)已知:如图,点B、A、E在一条直线上,∠1=∠B.
求证:∠2=∠C.
A
B
C
D
E
1
2
证明 ∵∠1=∠B( )
∴AD∥BC( )
∴∠2=∠C( )
已知
同位角相等,两直线平行
两直线平行,内错角相等
(2)已知,如图,∠1=∠2.求证:AB∥CD
A
B
C
D
E
F
1
2
3
证明 ∵∠1=∠2( )
又∵∠2∥∠3( )
∴∠1=∠3( )
∴AB//CD( )
已知
对顶角相等
等量代换
同位角相等,两直线平行
A
B
C
D
E
F
1
2
2.已知:如图,DC//AB,DF平分∠CDB,BE平分∠ABD.
求证:∠1 = ∠2.
证明 ∵DC//AB(已知 )
∴∠ABD=∠CDB.
(两直线平行,内错角相等)
又 ∵DF平分∠CDB,(已知)
BE平分∠ABD,(已知)
∴∠1=∠2.(等量代换)
∴∠1= ∠CDB,(角平分线的定义)
∠2= ∠ABD. (角平分线的定义)
3.已知:如图,直线AB与直线CD相交于点O,∠AOC与∠BOD是对顶角.求证:∠AOC =∠BOD.
证明:
∴ ∠AOB与∠COD都是平角(平角的定义 ),
∴ ∠AOC+∠AOD=180°,
∴ ∠AOC =∠BOD (同角的补角相等 ).
∵直线AB与直线CD相交于点O,
∠BOD+∠AOD=180°,
4.已知,如图:∠1=∠B,求证:∠2=∠C.
A
B
C
D
E
1
2
证明:∵∠1=∠B(已知),
∴AE∥BC(同位角相等,两直线平行),
∴∠2=∠(两直线平行,内错角相等).
课堂小结
证明
定理:经过证明的真命题称为定理.
证明:除了公理外,其他真命题的正确性都通过推理的方法证实.推理的过程称为证明.
