沪科版八年级数学上册 14.2.1 全等三角形的判定定理 课件(共22张PPT)
文档属性
| 名称 | 沪科版八年级数学上册 14.2.1 全等三角形的判定定理 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 427.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 12:08:09 | ||
图片预览







文档简介
(共22张PPT)
第十四章 全等三角形
14.2 全等三角形的判定
第1课时 三角形全等的判定1
旧知回顾
导入新课
答:能够完全重合的两个三角形叫做全等三角形.
1.什么是全等三角形?全等三角形性质是什么?
全等三角形对应边相等,对应角相等.
2.如图,如果△ABC≌△FED,请说出对应的边、对应顶点、对应角.
答:对应边:AC和DF,BC和ED,AB和FE;
对应角:∠A和∠F,∠B和∠E,∠ACB和∠FDE.
对应顶点:点A与点F,点C与点D,点B与点E;
探究新知
操作
三角形有六个基本元素(三边和三个角),只给定其中的一个元素或两个元素,能够确定一个三角形的形状和大小吗?通过画图,说明你的判断。
1.只给定一个元素
①一条边长4cm,
②一个角为45 .
①
②
只给定三角形的一个元素,无法确定一个三角形的形状。
解:如图所示
2.只给定两个元素
①两条边分别长4cm、5cm,
②一条边长为4cm,一个角为45 ,
③ 两个角分别为45 、60 .
只给定三角形的两个元素,也无法确定一个三角形的形状。
那还需增加什么条件才可唯一确定一个三角形呢?
①
②
③
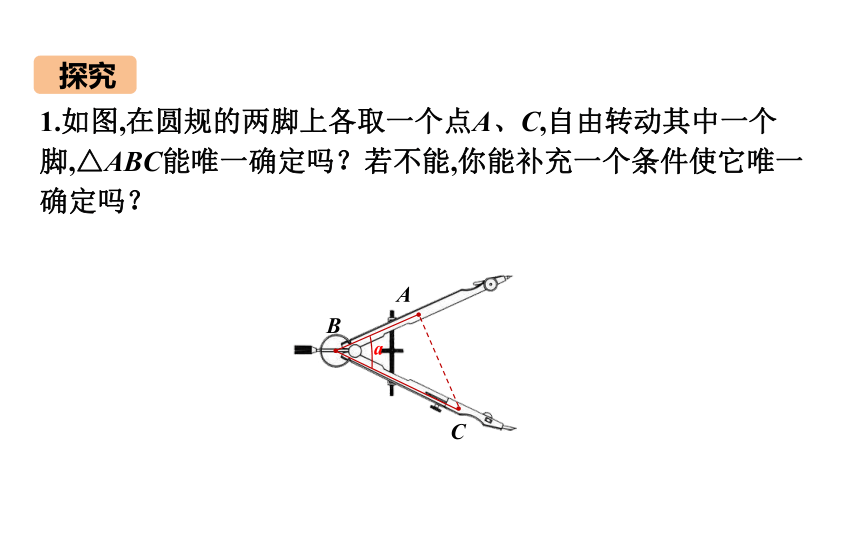
1.如图,在圆规的两脚上各取一个点A、C,自由转动其中一个脚,△ABC能唯一确定吗?若不能,你能补充一个条件使它唯一确定吗?
探究
A
C
B
a
2.如图,将两块三角尺的一条直角边放置在同一直线l上平移,其中∠B, ∠ C已知,并记两块三角尺斜边的交点为A,沿着直线l分别向左右移动两个三角尺,获得的△ABC能唯一确定吗
那么还需增加什么条件才可使△ABC唯一确定?
A
B
C
l
A
B
C
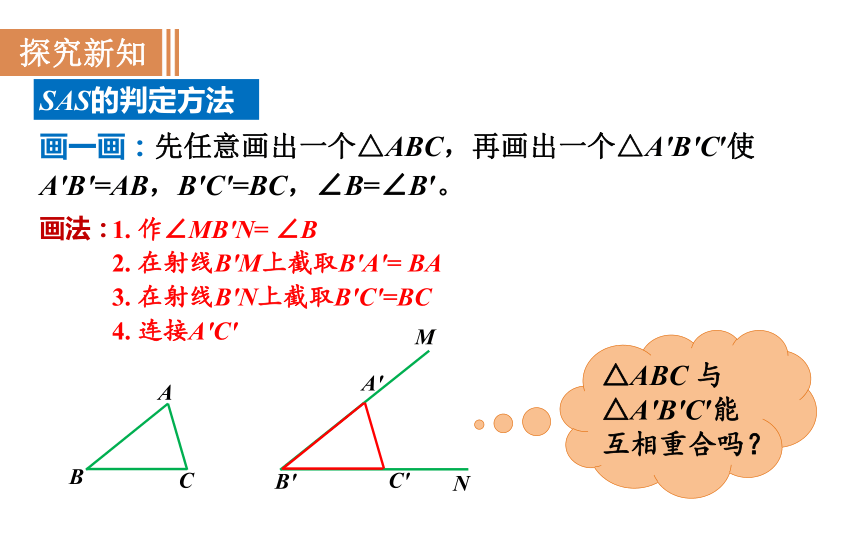
SAS的判定方法
探究新知
画法:
2. 在射线B′M上截取B′A′= BA
3. 在射线B′N上截取B′C′=BC
1. 作∠MB′N= ∠B
4. 连接A′C′
A
B
C
A′
B′
C′
M
N
△ABC 与△A′B′C′能互相重合吗?
画一画:先任意画出一个△ABC,再画出一个△A′B′C′使A′B′=AB,B′C′=BC,∠B=∠B′。
知识归纳
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
两边和它们的夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS ”).
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
三角形全等判定方法1
例题与练习
已知,如图,AD∥CB , AD= CB,求证 △ ADC ≌△ CBA.
证明:∵AD∥CB
在△ADC 和△ CBA中,
∴ △ ADC ≌△ CBA ( SAS)
A
B
C
D
∴∠DAC=∠BCA.
(两直线平行,内错角相等)
例
AD=CB(已知),
∠DAC=∠BAC(已证),
AC=CA(公共边),
∵
如图,AC和BD相交于点O,若OA=OD,用“SAS”证明△AOB≌△DOC还需 ( )
A.AB=DC B.OB=OC
C.∠C=∠D D.∠AOB=∠DOC
B
典例
如图①,点B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条件 ,便可根据“SAS”使△ABC≌△DEF.
AB=DE
仿例1
如图②,已知:AB=DB,CB=EB,∠1=∠2,则∠A= .
∠D
仿例2
SAS的判定与全等三角形性质综合运用
如图,在湖泊的岸边有A、B,难以直接量出A, B两点间的距离,你能设计一种量出A, B间距的方案吗?说明你这样设计的理由.
例
解:在岸上取可以直接到达A,B的一点C,
A
B
C
·
B′
A′
连接AC,延长AC到点A′,使A′C=AC;
连接BC,并延长BC到点B′,使B′C=BC.
连接A′ B′,量出的长度,就是AB两点间距离.
证明:在△ABC与△A′B′C中,
∵
AC=A′C
∠ACB= ∠ A′C B′,(对顶角相等)
BC=B′C
∴△ABC≌△A′B′C.(SAS)
∴A′B′=AB.(全等三角形对应边相等)
A
B
C
·
B′
A′
已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
典例
已知,如图所示,C为BE上一点,点A、D分别在BC两侧,AB∥ED,AB=CE,BC=ED,若∠ACB=30°,∠E=45°,则∠ACD= .
105°
仿例
随堂练习
1.如图,已知AB=AC,AD=AE.
求证:∠B=∠C.
B
C
D
E
A
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
AB=AC(已知)
∠A=∠A(公共角)
AD=AE (已知)
2.已知:如图, AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
证明:
OA=OC(已知)
∠AOB =∠COD (对顶角相等)
OB=OD (已知)
∵
∴△COD≌△AOB(SAS)
∴∠C=∠A(全等三角形对应角相等)
∴ DC∥AB (内错角相等的两条直线平行)
D
C
O
A
B
3.已知:如图,AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
证明:
在△CAE和△BAD 中
AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(SAS)
1
2
A
C
B
E
D
∵∠1=∠2(已知)
∴∠1+∠BAE = ∠2+∠BAE(等式的性质)
即 ∠BAD= ∠CAE
4.已知:如图, AB=CB,∠1= ∠2.
求证:(1) AD=CD; (2) DB 平分∠ADC.
A
D
B
C
1
2
4
3
在△ABD与△CBD中
证明:
∴△ABD≌△CBD(SAS)
AB=CB (已知)
∠1=∠2 (已知)
BD=BD (公共边)
∴AD =CD,∠3 =∠4
∴DB 平分∠ADC.
5.如图, 点E、F在AC上, AD//BC, AD=CB, AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴ ∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,即AF=CE.
AD=CB
∠A=∠C
AF=CE
(已知),
(已证),
(已证),
内容
有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
应用
注意
边角边
课堂小结
为证明线段和角相等提供了新的证法
1.已知两边,必须找“夹角”
2. 已知一角和这角的一夹边,必须找这角的另一夹边
第十四章 全等三角形
14.2 全等三角形的判定
第1课时 三角形全等的判定1
旧知回顾
导入新课
答:能够完全重合的两个三角形叫做全等三角形.
1.什么是全等三角形?全等三角形性质是什么?
全等三角形对应边相等,对应角相等.
2.如图,如果△ABC≌△FED,请说出对应的边、对应顶点、对应角.
答:对应边:AC和DF,BC和ED,AB和FE;
对应角:∠A和∠F,∠B和∠E,∠ACB和∠FDE.
对应顶点:点A与点F,点C与点D,点B与点E;
探究新知
操作
三角形有六个基本元素(三边和三个角),只给定其中的一个元素或两个元素,能够确定一个三角形的形状和大小吗?通过画图,说明你的判断。
1.只给定一个元素
①一条边长4cm,
②一个角为45 .
①
②
只给定三角形的一个元素,无法确定一个三角形的形状。
解:如图所示
2.只给定两个元素
①两条边分别长4cm、5cm,
②一条边长为4cm,一个角为45 ,
③ 两个角分别为45 、60 .
只给定三角形的两个元素,也无法确定一个三角形的形状。
那还需增加什么条件才可唯一确定一个三角形呢?
①
②
③
1.如图,在圆规的两脚上各取一个点A、C,自由转动其中一个脚,△ABC能唯一确定吗?若不能,你能补充一个条件使它唯一确定吗?
探究
A
C
B
a
2.如图,将两块三角尺的一条直角边放置在同一直线l上平移,其中∠B, ∠ C已知,并记两块三角尺斜边的交点为A,沿着直线l分别向左右移动两个三角尺,获得的△ABC能唯一确定吗
那么还需增加什么条件才可使△ABC唯一确定?
A
B
C
l
A
B
C
SAS的判定方法
探究新知
画法:
2. 在射线B′M上截取B′A′= BA
3. 在射线B′N上截取B′C′=BC
1. 作∠MB′N= ∠B
4. 连接A′C′
A
B
C
A′
B′
C′
M
N
△ABC 与△A′B′C′能互相重合吗?
画一画:先任意画出一个△ABC,再画出一个△A′B′C′使A′B′=AB,B′C′=BC,∠B=∠B′。
知识归纳
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
两边和它们的夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS ”).
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
三角形全等判定方法1
例题与练习
已知,如图,AD∥CB , AD= CB,求证 △ ADC ≌△ CBA.
证明:∵AD∥CB
在△ADC 和△ CBA中,
∴ △ ADC ≌△ CBA ( SAS)
A
B
C
D
∴∠DAC=∠BCA.
(两直线平行,内错角相等)
例
AD=CB(已知),
∠DAC=∠BAC(已证),
AC=CA(公共边),
∵
如图,AC和BD相交于点O,若OA=OD,用“SAS”证明△AOB≌△DOC还需 ( )
A.AB=DC B.OB=OC
C.∠C=∠D D.∠AOB=∠DOC
B
典例
如图①,点B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条件 ,便可根据“SAS”使△ABC≌△DEF.
AB=DE
仿例1
如图②,已知:AB=DB,CB=EB,∠1=∠2,则∠A= .
∠D
仿例2
SAS的判定与全等三角形性质综合运用
如图,在湖泊的岸边有A、B,难以直接量出A, B两点间的距离,你能设计一种量出A, B间距的方案吗?说明你这样设计的理由.
例
解:在岸上取可以直接到达A,B的一点C,
A
B
C
·
B′
A′
连接AC,延长AC到点A′,使A′C=AC;
连接BC,并延长BC到点B′,使B′C=BC.
连接A′ B′,量出的长度,就是AB两点间距离.
证明:在△ABC与△A′B′C中,
∵
AC=A′C
∠ACB= ∠ A′C B′,(对顶角相等)
BC=B′C
∴△ABC≌△A′B′C.(SAS)
∴A′B′=AB.(全等三角形对应边相等)
A
B
C
·
B′
A′
已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
典例
已知,如图所示,C为BE上一点,点A、D分别在BC两侧,AB∥ED,AB=CE,BC=ED,若∠ACB=30°,∠E=45°,则∠ACD= .
105°
仿例
随堂练习
1.如图,已知AB=AC,AD=AE.
求证:∠B=∠C.
B
C
D
E
A
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
AB=AC(已知)
∠A=∠A(公共角)
AD=AE (已知)
2.已知:如图, AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
证明:
OA=OC(已知)
∠AOB =∠COD (对顶角相等)
OB=OD (已知)
∵
∴△COD≌△AOB(SAS)
∴∠C=∠A(全等三角形对应角相等)
∴ DC∥AB (内错角相等的两条直线平行)
D
C
O
A
B
3.已知:如图,AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
证明:
在△CAE和△BAD 中
AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(SAS)
1
2
A
C
B
E
D
∵∠1=∠2(已知)
∴∠1+∠BAE = ∠2+∠BAE(等式的性质)
即 ∠BAD= ∠CAE
4.已知:如图, AB=CB,∠1= ∠2.
求证:(1) AD=CD; (2) DB 平分∠ADC.
A
D
B
C
1
2
4
3
在△ABD与△CBD中
证明:
∴△ABD≌△CBD(SAS)
AB=CB (已知)
∠1=∠2 (已知)
BD=BD (公共边)
∴AD =CD,∠3 =∠4
∴DB 平分∠ADC.
5.如图, 点E、F在AC上, AD//BC, AD=CB, AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴ ∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,即AF=CE.
AD=CB
∠A=∠C
AF=CE
(已知),
(已证),
(已证),
内容
有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
应用
注意
边角边
课堂小结
为证明线段和角相等提供了新的证法
1.已知两边,必须找“夹角”
2. 已知一角和这角的一夹边,必须找这角的另一夹边
