沪科版八年级数学上册14.2.4 其他判定两个三角形全等的条件 课件 (共22张PPT)
文档属性
| 名称 | 沪科版八年级数学上册14.2.4 其他判定两个三角形全等的条件 课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 12:09:25 | ||
图片预览






文档简介
(共22张PPT)
第十四章 全等三角形
14.2 三角形全等的判定
第4课时 其他判定两个三角形全等的条件
旧知回顾
导入新课
我们学过的三角形全等的判定方法有哪几种?如何叙述?
答:SAS,ASA,SSS共三种.
有两边及其夹角对应相等的两个三角形全等(简称“边角边”“SAS”);
有两角和它们的夹边对应相等的两个三角形全等(简称“角边角”“ASA”);
有三边对应相等的两个三角形全等(简称“边边边”“SSS”).
探究新知
AAS的判定方法
给出三个条件画三角形时,共有六种情况,我们已经研究了三种:(SAS 、ASA 、 SSS )每种情况下作出的三角形都全等,剩下三种情况画出的三角形是否全等?
(1)三角相等;
(2)两边和其中一边的对角对应相等;
(3)两角和其中一角的对边对应相等.
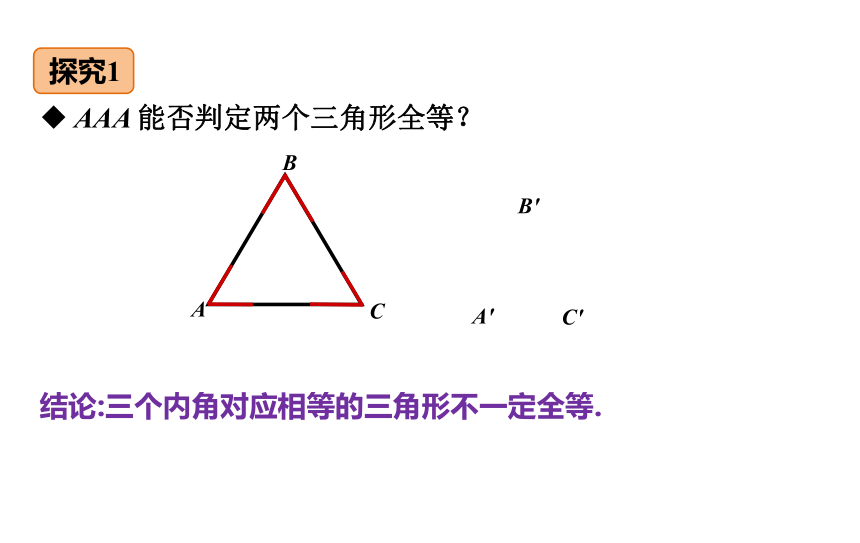
AAA 能否判定两个三角形全等?
探究1
A
B
C
A′
B′
C′
结论:三个内角对应相等的三角形不一定全等.
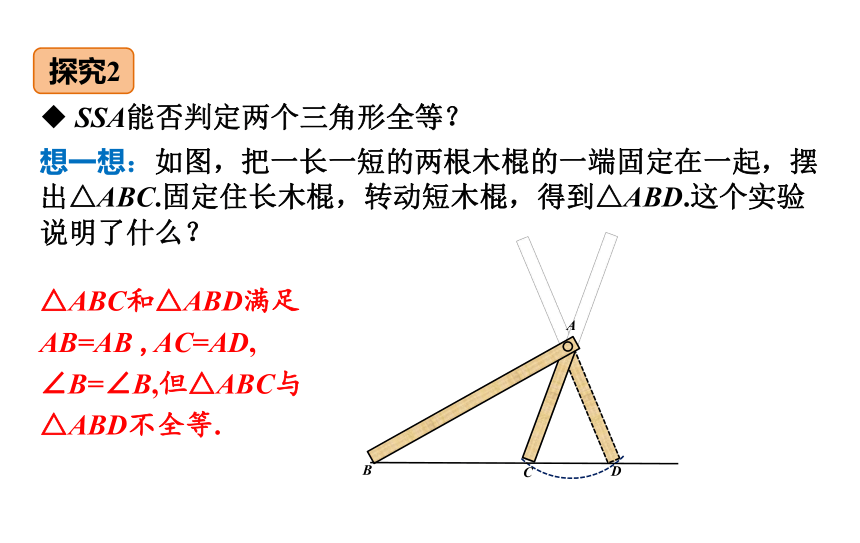
想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
SSA能否判定两个三角形全等?
探究2
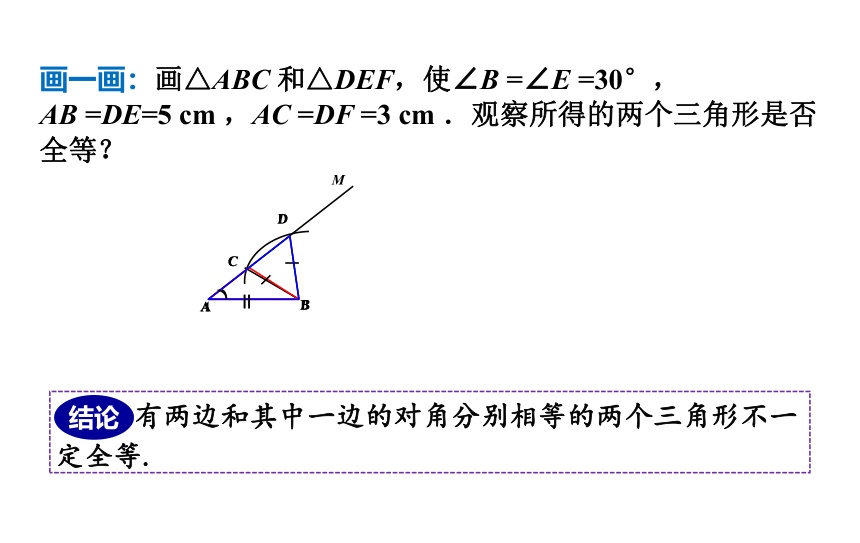
画一画:画△ABC 和△DEF,使∠B =∠E =30°,
AB =DE=5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全等?
A
B
M
C
D
A
B
C
A
B
D
有两边和其中一边的对角分别相等的两个三角形不一定全等.
结论
探究3
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
60°
45°
AAS能否判定两个三角形全等?
60°
45°
思考:这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?
75°
知识归纳
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
∴ △ABC≌△ A′ B′ C′ (AAS).
A
B
C
A ′
B ′
C ′
例题与练习
典例
如图,∠E=∠F=90°,∠B=∠C,AE=AF,推出△ABE≌△ACF的根据是 .
AAS
仿例1
如图,在△ABC和△DEF中,点B、F、C、E在同一条直线上,BF=CE,AC∥DF,请你添加一个条件,使△ABC≌△DEF,这个条件是 (答案不唯一)(判定的理由是AAS).
∠A=∠D
如图,已知∠BAC=∠DAE,∠ABD=∠ACE,
BD=CE,试判断AB与AC的大小.
证明:AB=AC.
证明 :∵∠BAC=∠DAE,
仿例2
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
∠BAD=∠CAE,
∠ABD=∠ACE,
BD=CE,
∴△ABD≌△ACE(AAS),
∴AB=AC.
例
已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED, AC∥EF ,求证:△ABC≌△EDF.
E
D
C
F
B
A
证明 ∵ AB∥ED, AC∥EF
AAS的判定与性质的综合运用
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
仿例1
如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.求证:AB=BF.
证明:∵EF⊥AC,
∴∠FEC=90°,
∴∠F+∠C=90°,
∵∠ABC=90°,
∴∠A+∠C=90°,
∴∠A=∠F,
在△ABC和△FBD中,
∴△ABC≌△FBD(AAS),
∴AB=BF.
如图,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E,问:BD、DE、CE有怎样的数量关系?说出理由.
解:BD=DE+CE.
仿例2
理由:∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
又∵∠BAC=90°,
∴∠BAD+∠ABD=90°,∠BAD+∠EAC=90°,
∴∠ABD=∠CAE.
∠A=4,
∠ABC=∠FBD,
BC=DC,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,AD+DE,
∴BD=DE+CE.
随堂练习
分别写出下列两题中符合已知条件的全等三角形,并说明全等的依据.
A
B
C
D
E
1
△ABC≌△CDE(AAS)
(2)已知:如图,AB=DB,BC=BE,∠ABC=∠DBE.
A
B
D
C
E
△ABC≌△DBE(SAS)
(1)已知:如图,点C在BD上, ∠B=∠D=90°,且AB=CD,∠1=∠E;
2.如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
求证:(1)△BDA≌△AEC;
证明:∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
3.如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
(ASA)
或 (AAS)
或 (SAS)
∠ACB=∠DBC
∠A=∠D
AB=DC
A
B
C
D
4.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知), ∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
三角形全等的“AAS”判定:两角分别相等且其中一组等角的对边相等的两个三角形全等
其他判定两个三角形全等的条件
课堂小结
“AAA”“SSA”不能作为两三角形全等判定依据
第十四章 全等三角形
14.2 三角形全等的判定
第4课时 其他判定两个三角形全等的条件
旧知回顾
导入新课
我们学过的三角形全等的判定方法有哪几种?如何叙述?
答:SAS,ASA,SSS共三种.
有两边及其夹角对应相等的两个三角形全等(简称“边角边”“SAS”);
有两角和它们的夹边对应相等的两个三角形全等(简称“角边角”“ASA”);
有三边对应相等的两个三角形全等(简称“边边边”“SSS”).
探究新知
AAS的判定方法
给出三个条件画三角形时,共有六种情况,我们已经研究了三种:(SAS 、ASA 、 SSS )每种情况下作出的三角形都全等,剩下三种情况画出的三角形是否全等?
(1)三角相等;
(2)两边和其中一边的对角对应相等;
(3)两角和其中一角的对边对应相等.
AAA 能否判定两个三角形全等?
探究1
A
B
C
A′
B′
C′
结论:三个内角对应相等的三角形不一定全等.
想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
SSA能否判定两个三角形全等?
探究2
画一画:画△ABC 和△DEF,使∠B =∠E =30°,
AB =DE=5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全等?
A
B
M
C
D
A
B
C
A
B
D
有两边和其中一边的对角分别相等的两个三角形不一定全等.
结论
探究3
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
60°
45°
AAS能否判定两个三角形全等?
60°
45°
思考:这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?
75°
知识归纳
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
∴ △ABC≌△ A′ B′ C′ (AAS).
A
B
C
A ′
B ′
C ′
例题与练习
典例
如图,∠E=∠F=90°,∠B=∠C,AE=AF,推出△ABE≌△ACF的根据是 .
AAS
仿例1
如图,在△ABC和△DEF中,点B、F、C、E在同一条直线上,BF=CE,AC∥DF,请你添加一个条件,使△ABC≌△DEF,这个条件是 (答案不唯一)(判定的理由是AAS).
∠A=∠D
如图,已知∠BAC=∠DAE,∠ABD=∠ACE,
BD=CE,试判断AB与AC的大小.
证明:AB=AC.
证明 :∵∠BAC=∠DAE,
仿例2
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
∠BAD=∠CAE,
∠ABD=∠ACE,
BD=CE,
∴△ABD≌△ACE(AAS),
∴AB=AC.
例
已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED, AC∥EF ,求证:△ABC≌△EDF.
E
D
C
F
B
A
证明 ∵ AB∥ED, AC∥EF
AAS的判定与性质的综合运用
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
仿例1
如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.求证:AB=BF.
证明:∵EF⊥AC,
∴∠FEC=90°,
∴∠F+∠C=90°,
∵∠ABC=90°,
∴∠A+∠C=90°,
∴∠A=∠F,
在△ABC和△FBD中,
∴△ABC≌△FBD(AAS),
∴AB=BF.
如图,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E,问:BD、DE、CE有怎样的数量关系?说出理由.
解:BD=DE+CE.
仿例2
理由:∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
又∵∠BAC=90°,
∴∠BAD+∠ABD=90°,∠BAD+∠EAC=90°,
∴∠ABD=∠CAE.
∠A=4,
∠ABC=∠FBD,
BC=DC,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,AD+DE,
∴BD=DE+CE.
随堂练习
分别写出下列两题中符合已知条件的全等三角形,并说明全等的依据.
A
B
C
D
E
1
△ABC≌△CDE(AAS)
(2)已知:如图,AB=DB,BC=BE,∠ABC=∠DBE.
A
B
D
C
E
△ABC≌△DBE(SAS)
(1)已知:如图,点C在BD上, ∠B=∠D=90°,且AB=CD,∠1=∠E;
2.如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
求证:(1)△BDA≌△AEC;
证明:∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
3.如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
(ASA)
或 (AAS)
或 (SAS)
∠ACB=∠DBC
∠A=∠D
AB=DC
A
B
C
D
4.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知), ∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
三角形全等的“AAS”判定:两角分别相等且其中一组等角的对边相等的两个三角形全等
其他判定两个三角形全等的条件
课堂小结
“AAA”“SSA”不能作为两三角形全等判定依据
