人教版数学九年级上册 22.1.3二次函数yax-h?k的图像和性质 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级上册 22.1.3二次函数yax-h?k的图像和性质 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第3课时 二次函数y=a(x-h) +k的图像和性质
22.1.3 二次函数y=a(x-h) +k的图像和性质
第二十二章 二次函数
桃子沙
侯
3
1.抛物线y=a(x一h)2十k与y=ax2形状相同
位置
不同,把抛物线y=ax2向上(下)和向
左(右)平移,可以得到抛物线y=α(x一h)2十k,
平移的方向、距离要根据,飞的值来决定,
2.抛物线y=a(x一h)2十k有如下特点:①当a>0
时,开口向上;当a≤0时,开口向下;②对
称轴是直线x=h
;③顶点坐标是
(h,k).
1.(黔南州期末)抛物线y=(x一3)2十4的顶点坐
标是(D)
A.(-3,4)
B.(-3,-4)
C.(3,-4)
D.(3,4)
2.下列关于抛物线y=3(x一1)2十1的说法,正确
的是(D)
A.开口向下
B.对称轴是x=一1
C.顶点坐标是(一1,1)
D.有最小值y=1
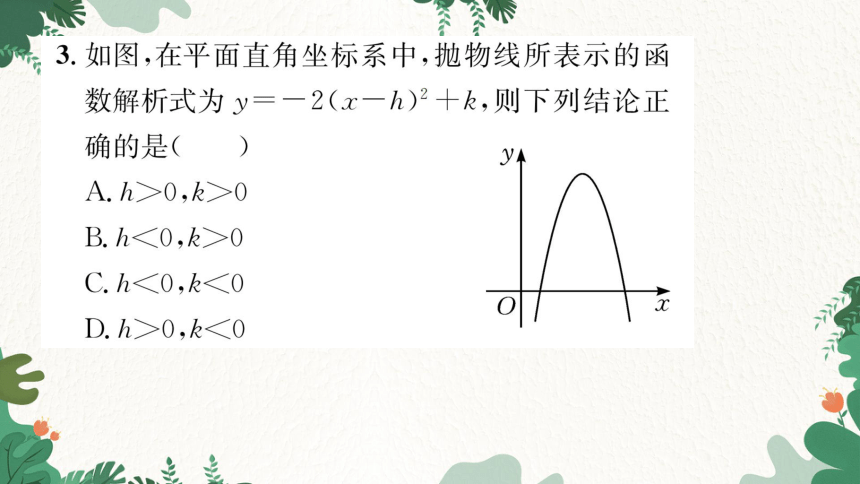
3.如图,在平面直角坐标系中,抛物线所表示的函
数解析式为y=一2(x一h)2十k,则下列结论正
确的是(A)
A.h>0,k>0
B.h<0,k>0
C.h<0,k<0
D.h>0,k<0
6.填表.
函数解析式
开口方向
对称轴
顶点
y=(x+1)2+2
向上
=一1
(-1,2)
y=-2(x-3)2-3
向下
K=3
(3,-3)
y=5(x-2)2+4
向上
x=2
(2,4)
y=-3(x+1)2-6
向下
x=一1
(-1,-6)
7.在平面直角坐标系中,如果抛物线y=3x2十3不
动,而把x轴、y轴分别向上、向右平移2个单位
长度,那么在新坐标系下抛物线的函数解析式是
(B)
A.y=3(x-2)2+5
B.y=3(x+2)2+1
C.y=3(x+2)2+5
D.y=3(x-2)2+1
9.在直角坐标系巾画出函数y=(x一3)2-1的
图象.
(1)指出该函数图象的开口方向、对称轴和顶点;
(2)说明该函数图象如何平移能与二次函数y一
的图象重合;
y
本321
-2-1
:O1X3:4以56:78
℃
(1)该函数图象的开口向上,对称轴为x=3,顶点
坐标为(3,一1).
(2)二次函数y=2(x-3)2-1的图象向左平移
3个单位长度,再向上平移1个单位长度得到二
次函数y=2x2
的图象。
(3)当≥3时,y随x的增大而增大;当x≤3时,
y随x的增大而减小.
第3课时 二次函数y=a(x-h) +k的图像和性质
22.1.3 二次函数y=a(x-h) +k的图像和性质
第二十二章 二次函数
桃子沙
侯
3
1.抛物线y=a(x一h)2十k与y=ax2形状相同
位置
不同,把抛物线y=ax2向上(下)和向
左(右)平移,可以得到抛物线y=α(x一h)2十k,
平移的方向、距离要根据,飞的值来决定,
2.抛物线y=a(x一h)2十k有如下特点:①当a>0
时,开口向上;当a≤0时,开口向下;②对
称轴是直线x=h
;③顶点坐标是
(h,k).
1.(黔南州期末)抛物线y=(x一3)2十4的顶点坐
标是(D)
A.(-3,4)
B.(-3,-4)
C.(3,-4)
D.(3,4)
2.下列关于抛物线y=3(x一1)2十1的说法,正确
的是(D)
A.开口向下
B.对称轴是x=一1
C.顶点坐标是(一1,1)
D.有最小值y=1
3.如图,在平面直角坐标系中,抛物线所表示的函
数解析式为y=一2(x一h)2十k,则下列结论正
确的是(A)
A.h>0,k>0
B.h<0,k>0
C.h<0,k<0
D.h>0,k<0
6.填表.
函数解析式
开口方向
对称轴
顶点
y=(x+1)2+2
向上
=一1
(-1,2)
y=-2(x-3)2-3
向下
K=3
(3,-3)
y=5(x-2)2+4
向上
x=2
(2,4)
y=-3(x+1)2-6
向下
x=一1
(-1,-6)
7.在平面直角坐标系中,如果抛物线y=3x2十3不
动,而把x轴、y轴分别向上、向右平移2个单位
长度,那么在新坐标系下抛物线的函数解析式是
(B)
A.y=3(x-2)2+5
B.y=3(x+2)2+1
C.y=3(x+2)2+5
D.y=3(x-2)2+1
9.在直角坐标系巾画出函数y=(x一3)2-1的
图象.
(1)指出该函数图象的开口方向、对称轴和顶点;
(2)说明该函数图象如何平移能与二次函数y一
的图象重合;
y
本321
-2-1
:O1X3:4以56:78
℃
(1)该函数图象的开口向上,对称轴为x=3,顶点
坐标为(3,一1).
(2)二次函数y=2(x-3)2-1的图象向左平移
3个单位长度,再向上平移1个单位长度得到二
次函数y=2x2
的图象。
(3)当≥3时,y随x的增大而增大;当x≤3时,
y随x的增大而减小.
同课章节目录
