沪科版九年级数学上册21.4.1 二次函数的应用(第1课时)课件 (共22张PPT)
文档属性
| 名称 | 沪科版九年级数学上册21.4.1 二次函数的应用(第1课时)课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:10:47 | ||
图片预览






文档简介
(共22张PPT)
第二十一章 二次函数与反比例函数
21.4 二次函数的应用
第1课时 二次函数的应用(1)
y=-4(x2-20x+102-102)
=-4(x-10)2+400
当x=10时,y最大值=400
旧知回顾
利用配方法求函数 y=-4x2+80x 的最大值.
求二次函数的最大值(或最小值)
(1) 当自变量x为全体实数时,二次函数 y=ax2+bx+c 的最值是多少?
(2) 当自变量x有限制时,二次函数 y=ax2+bx+c 的最值如何确定?
问题
当a>0时,有 y最小值= ,此时x=- ;
当a<0时,有 y最大值= ,此时x=- .
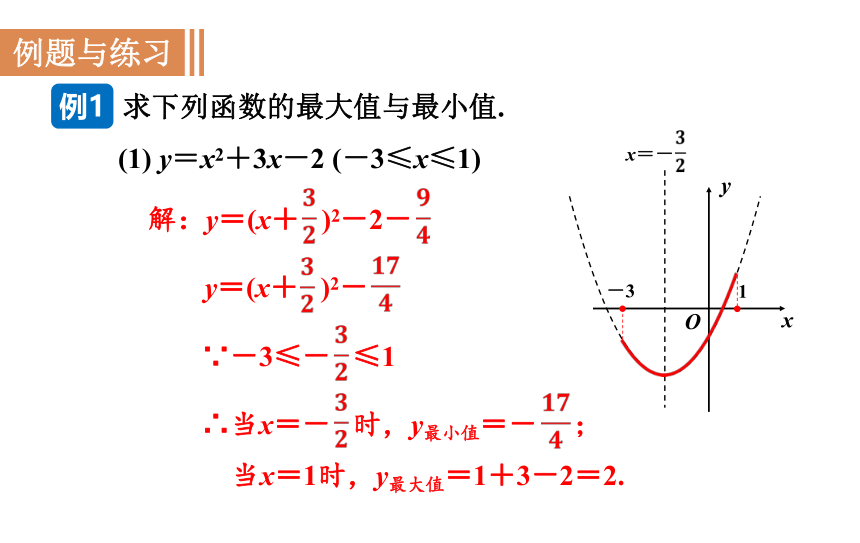
求下列函数的最大值与最小值.
(1) y=x2+3x-2 (-3≤x≤1)
解:y=(x+ )2-2-
y=(x+ )2-
∵-3≤- ≤1
∴当x=- 时,y最小值=- ;
当x=1时,y最大值=1+3-2=2.
x
O
y
-3
1
x=-
例1
(2) y=- x2-2x+1 (-3≤x≤1)
解:y=- (x+5)2+6
∵-5<-3
即x在对称轴的右侧.
函数的值随着x的增大而减小.
∴当x=-3时,y最大值= ;
当x=1时,y最小值=- .
x
O
y
-3
1
x=-5
当自变量的范围有限制时,二次函数 y=ax2+bx+c 的最值可以根据以下步骤来确定:
(1) 配方,求二次函数的顶点坐标及对称轴.
(2) 画出函数图象,标明对称轴,并在横坐标上标明x的取值范围.
(3) 判断x的取值范围与对称轴的位置关系.根据二次函数的性质,确定当x取何值时函数有最大或最小值.然后根据x的值,求出函数的最值.
用二次函数解决图形面积最优值
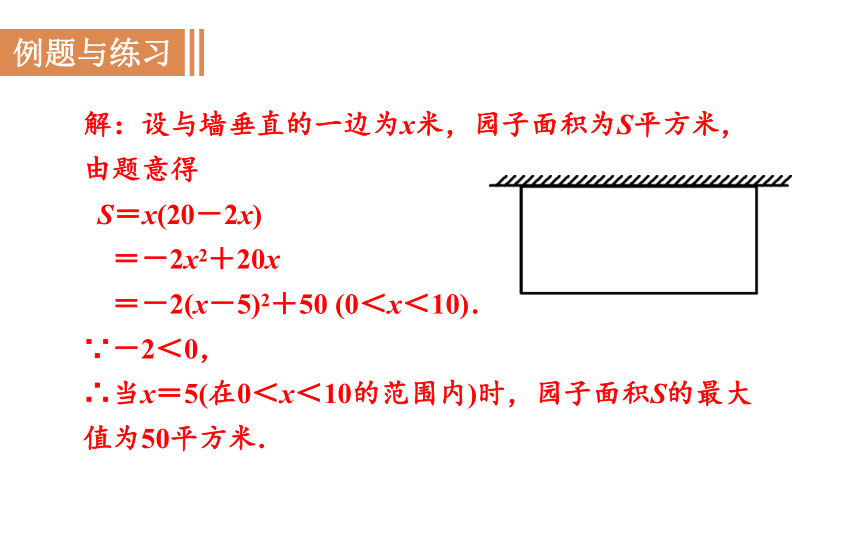
如图,用长20米的篱笆,一面靠墙(墙长不限)围成一个长方形的园子,怎么围才能使园子的面积最大?最大面积是多少?
例2
解:设与墙垂直的一边为x米,园子面积为S平方米,由题意得
S=x(20-2x)
=-2x2+20x
=-2(x-5)2+50 (0<x<10).
∵-2<0,
∴当x=5(在0<x<10的范围内)时,园子面积S的最大值为50平方米.
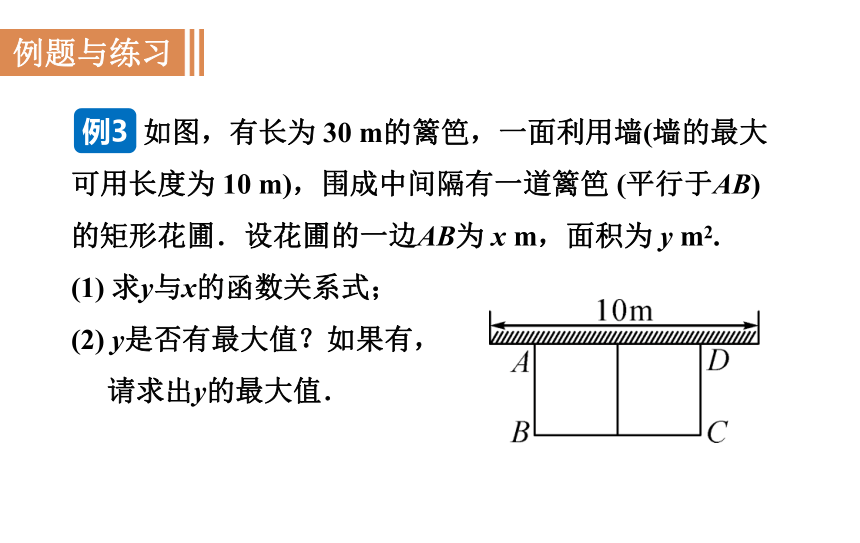
如图,有长为 30 m的篱笆,一面利用墙(墙的最大可用长度为 10 m),围成中间隔有一道篱笆 (平行于AB)的矩形花圃.设花圃的一边AB为 x m,面积为 y m2.
(1) 求y与x的函数关系式;
(2) y是否有最大值?如果有,
请求出y的最大值.
例3
解:(1)由题意得:y=x(30-3x),即y=-3x2+30x.
(2)由题意得:0<30-3x≤10,即 ≤x<10.
对称轴为x= =- =5,
∵当x>5时,y随x的增大而减小.
∴当x= m时面积最大,
最大面积为 m2.
二次函数解决几何面积最值问题的方法:
(1) 求出函数解析式和自变量的取值范围;
(2) 配方变形,或利用公式求它的最大值或最小值;
(3) 检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
用二次函数解决拱桥类问题
如图是一个横断面为抛物线形状的拱桥.当水面宽为4 m时,拱顶(拱桥洞的最高点)离水面2 m,水面下降1 m时,水面宽度为多少米?
例4
解:建立如图所示的直角坐标,其中O点为拱顶,CD长为4 (m),AB的长度即为所求的水面宽度.
设抛物线解析式为y=ax2(a≠0),
由题意知D坐标为(2,-2),
代入y=ax2,得-2=4a,a=- ,
∴y=- x2,B点纵坐标为-3,
当y=-3时,- x2=-3,解得x=± ,
∴A(- ,-3),B( ,-3),AB=2 ,
∴当水面下降1米时,水面宽度为2 米.
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,
主悬钢索最低点离桥面的高度
为0.5 m.
例5
解:根据题意,得抛物线的顶点坐标为 (0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点 (450,81.5),代入上式,得
81.5=a·4502+0.5.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
解得 a= =
故所求表达式为
y= x2+0.5 (-450≤x≤450)
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100 m,50 m处垂直钢索的长.
解:当x=450-100=350 (m)时,得
当x=450-50=400 (m)时,得
y
x
O
-450
450
y= ×3502+0.5=49.5 (m)
y= ×4002+0.5=64.5 (m)
随堂练习
1.用一段长为 15 m的篱笆围成一个一边靠墙的矩形菜园,墙长为18 m,这个矩形菜园的最大面积是_______.
2.某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,则他在不弯腰的情况下在大棚内活动的范围是______米.
m2
随堂练习
3.如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿AB向B以2 cm/s的速度移动(不与点B重合),动点Q从点B开始BC以4 cm/s的速度移动(不与点C重合).
如果P、Q分别从A、B同时出发,那
么经过_____秒,四边形APQC的面积
最小.
A
B
C
P
Q
3
4.有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2
随堂练习
5.如图1,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(即NC=4.5米).当水位上涨刚好淹没小孔时,借助图2中的直角坐标系,求此时大孔的水面宽度EF.
图1
图2
随堂练习
解:设大孔对应的抛物线所对应的函数关系式为
y=ax2+6.
依题意,得B(10,0),代入102a+6=0.
解得a=-0.06,得y=-0.06x2+6.
当y=4.5时,-0.06x2+6=4.5,解得x=±5.
∴DF=5,EF=10,即水面宽度为10米.
图1
图2
随堂练习
图形面积最优值
拱桥类
问题
二次函数的应用(1)
1.关键:建立函数关系式
2.注意:最值有时不在顶点处,则要利用函数的增减性来确定
建立直角坐标系:
(1)能够将实际距离准确的转化
为点的坐标;
(2)选择运算简便的方法.
第二十一章 二次函数与反比例函数
21.4 二次函数的应用
第1课时 二次函数的应用(1)
y=-4(x2-20x+102-102)
=-4(x-10)2+400
当x=10时,y最大值=400
旧知回顾
利用配方法求函数 y=-4x2+80x 的最大值.
求二次函数的最大值(或最小值)
(1) 当自变量x为全体实数时,二次函数 y=ax2+bx+c 的最值是多少?
(2) 当自变量x有限制时,二次函数 y=ax2+bx+c 的最值如何确定?
问题
当a>0时,有 y最小值= ,此时x=- ;
当a<0时,有 y最大值= ,此时x=- .
求下列函数的最大值与最小值.
(1) y=x2+3x-2 (-3≤x≤1)
解:y=(x+ )2-2-
y=(x+ )2-
∵-3≤- ≤1
∴当x=- 时,y最小值=- ;
当x=1时,y最大值=1+3-2=2.
x
O
y
-3
1
x=-
例1
(2) y=- x2-2x+1 (-3≤x≤1)
解:y=- (x+5)2+6
∵-5<-3
即x在对称轴的右侧.
函数的值随着x的增大而减小.
∴当x=-3时,y最大值= ;
当x=1时,y最小值=- .
x
O
y
-3
1
x=-5
当自变量的范围有限制时,二次函数 y=ax2+bx+c 的最值可以根据以下步骤来确定:
(1) 配方,求二次函数的顶点坐标及对称轴.
(2) 画出函数图象,标明对称轴,并在横坐标上标明x的取值范围.
(3) 判断x的取值范围与对称轴的位置关系.根据二次函数的性质,确定当x取何值时函数有最大或最小值.然后根据x的值,求出函数的最值.
用二次函数解决图形面积最优值
如图,用长20米的篱笆,一面靠墙(墙长不限)围成一个长方形的园子,怎么围才能使园子的面积最大?最大面积是多少?
例2
解:设与墙垂直的一边为x米,园子面积为S平方米,由题意得
S=x(20-2x)
=-2x2+20x
=-2(x-5)2+50 (0<x<10).
∵-2<0,
∴当x=5(在0<x<10的范围内)时,园子面积S的最大值为50平方米.
如图,有长为 30 m的篱笆,一面利用墙(墙的最大可用长度为 10 m),围成中间隔有一道篱笆 (平行于AB)的矩形花圃.设花圃的一边AB为 x m,面积为 y m2.
(1) 求y与x的函数关系式;
(2) y是否有最大值?如果有,
请求出y的最大值.
例3
解:(1)由题意得:y=x(30-3x),即y=-3x2+30x.
(2)由题意得:0<30-3x≤10,即 ≤x<10.
对称轴为x= =- =5,
∵当x>5时,y随x的增大而减小.
∴当x= m时面积最大,
最大面积为 m2.
二次函数解决几何面积最值问题的方法:
(1) 求出函数解析式和自变量的取值范围;
(2) 配方变形,或利用公式求它的最大值或最小值;
(3) 检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
用二次函数解决拱桥类问题
如图是一个横断面为抛物线形状的拱桥.当水面宽为4 m时,拱顶(拱桥洞的最高点)离水面2 m,水面下降1 m时,水面宽度为多少米?
例4
解:建立如图所示的直角坐标,其中O点为拱顶,CD长为4 (m),AB的长度即为所求的水面宽度.
设抛物线解析式为y=ax2(a≠0),
由题意知D坐标为(2,-2),
代入y=ax2,得-2=4a,a=- ,
∴y=- x2,B点纵坐标为-3,
当y=-3时,- x2=-3,解得x=± ,
∴A(- ,-3),B( ,-3),AB=2 ,
∴当水面下降1米时,水面宽度为2 米.
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,
主悬钢索最低点离桥面的高度
为0.5 m.
例5
解:根据题意,得抛物线的顶点坐标为 (0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点 (450,81.5),代入上式,得
81.5=a·4502+0.5.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
解得 a= =
故所求表达式为
y= x2+0.5 (-450≤x≤450)
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100 m,50 m处垂直钢索的长.
解:当x=450-100=350 (m)时,得
当x=450-50=400 (m)时,得
y
x
O
-450
450
y= ×3502+0.5=49.5 (m)
y= ×4002+0.5=64.5 (m)
随堂练习
1.用一段长为 15 m的篱笆围成一个一边靠墙的矩形菜园,墙长为18 m,这个矩形菜园的最大面积是_______.
2.某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,则他在不弯腰的情况下在大棚内活动的范围是______米.
m2
随堂练习
3.如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿AB向B以2 cm/s的速度移动(不与点B重合),动点Q从点B开始BC以4 cm/s的速度移动(不与点C重合).
如果P、Q分别从A、B同时出发,那
么经过_____秒,四边形APQC的面积
最小.
A
B
C
P
Q
3
4.有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2
随堂练习
5.如图1,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(即NC=4.5米).当水位上涨刚好淹没小孔时,借助图2中的直角坐标系,求此时大孔的水面宽度EF.
图1
图2
随堂练习
解:设大孔对应的抛物线所对应的函数关系式为
y=ax2+6.
依题意,得B(10,0),代入102a+6=0.
解得a=-0.06,得y=-0.06x2+6.
当y=4.5时,-0.06x2+6=4.5,解得x=±5.
∴DF=5,EF=10,即水面宽度为10米.
图1
图2
随堂练习
图形面积最优值
拱桥类
问题
二次函数的应用(1)
1.关键:建立函数关系式
2.注意:最值有时不在顶点处,则要利用函数的增减性来确定
建立直角坐标系:
(1)能够将实际距离准确的转化
为点的坐标;
(2)选择运算简便的方法.
