沪科版九年级数学上册22.1.3 平行线分线段成比例定理及其推论 课件 (共21张PPT)
文档属性
| 名称 | 沪科版九年级数学上册22.1.3 平行线分线段成比例定理及其推论 课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:41:17 | ||
图片预览





文档简介
(共21张PPT)
第二十二章 相似形
22.1 比例线段
第3课时 平行线分线段成比例定理及其推论
旧知回顾
1.什么是平行线等分线段定理?
如果一组平行线在一条直线上截得的线段相等,那么它在另一条直线上截得的线段也相等.
2.求出下列各式中的x∶y.
(1)3x=5y (2)x= y (3)3∶x=5∶y
解:(1) = ;
(2) = ;
(3) =
旧知回顾
3.已知 = ,求 .
∴
=
=
,
解:∵
=
,
∴
=
,
=
∴
.
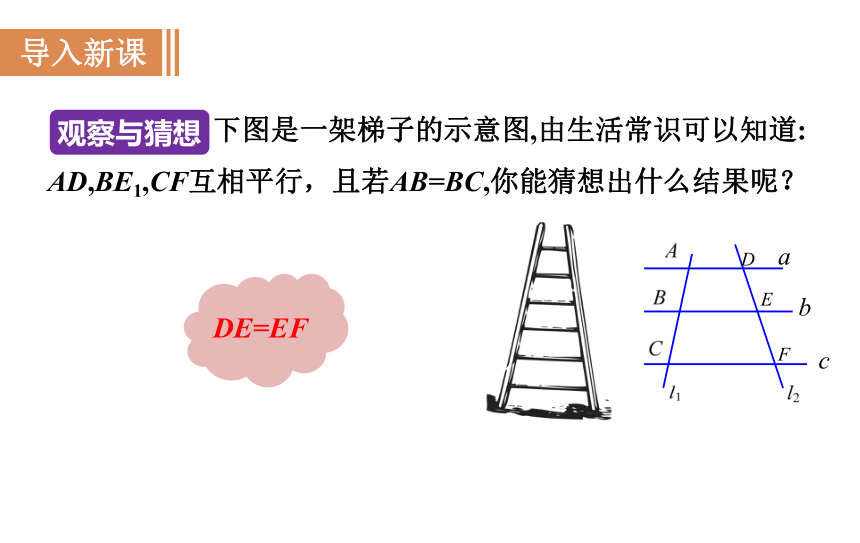
下图是一架梯子的示意图,由生活常识可以知道:
AD,BE1,CF互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
D
F
E
观察与猜想
DE=EF
什么是平行线分线段成比例定理,如何推导?
平行线分线段成比例定理推导与应用
解:如图,有一组平行线:l1∥l2∥l3…∥ln,
根据已学定理,可以得到:
如果A1A2=A2A3=…=An-1An,那么B1B2=B2B3=…Bn-1Bn.
另外,直线A1An与直线B1Bn被这一组平行线分别截于点A1,A2,…,An和点B1,B2,…,Bn.
如果设A1A2=A2A3=…An-1An=a,B1B2=B2B3=…Bn-1Bn=b,
容易得到:
=
=
,
.
所以有
=
=
=
,
符号语言
A1
A2
A3
B1
B2
B3
b
c
a
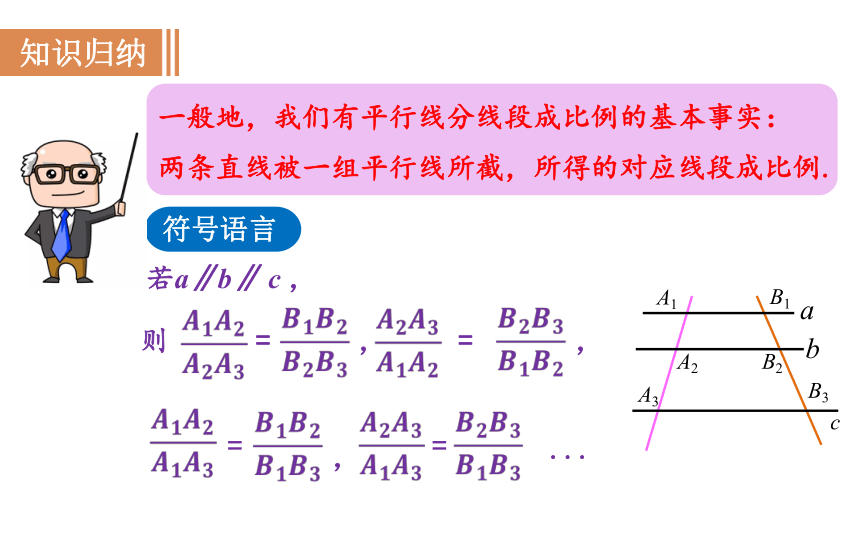
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
若a∥b∥ c ,
则 = , = ,
=
,
...
=
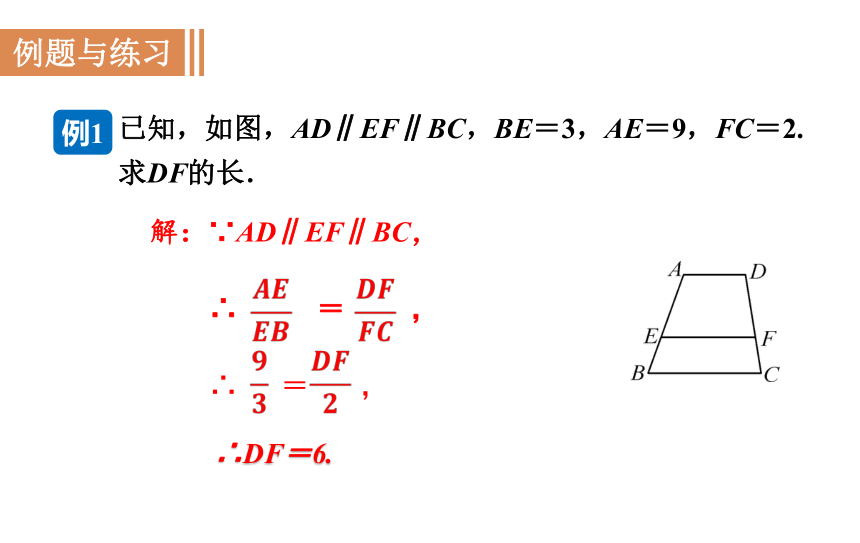
已知,如图,AD∥EF∥BC,BE=3,AE=9,FC=2.求DF的长.
解:∵AD∥EF∥BC,
例1
∴DF=6.
∴ = ,
∴ = ,
A
B
C
E
F
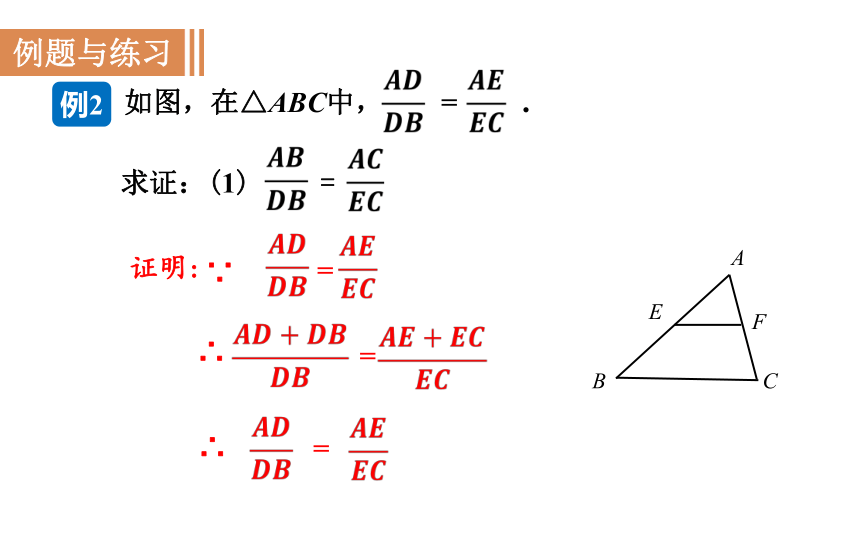
例2
如图,在△ABC中, = .
求证:(1)
=
证明:
∵
=
∴
=
∴
=
A
B
C
E
F
(2)
=
,
证明:
∵
=
,
=
.
∴
∴
=
.
=
∴
.
∴
=
.
证明:∵l1∥l2∥l3,
如图,已知l1∥l2∥l3, = ,求证 = .
例3
∴
=
=
,
∴
=
∴
=
,
∴
=
,
=
,
∴
平行线分线段成比例定理推论是什么?有哪些形式?如何证明?
平行于三角形一边的直线截其他两边(或两边延长线)所对的对应线段成比例,有三种形式,补齐图中第三条平行线可证.
平行线分线段成比例定理推论与应用
推论
如图,AD∥EG∥BC,AD=6,BC=9,AE∶AB=2∶3,求GF的长.
例4
∴ = ,
EG=6.
∵EF∥AD,
∴ = ,EF=2,
∴GF=EG-EF=6-2=4.
∵EG∥BC,
解:
证明:∵DE∥BC,
如图,△ABC中,DE∥BC,DF∥BE,求证 = .
例5
∴ = .
∵DF∥BE,
∴ = ,
∴ = .
解:过D作DH∥BE交AC于H.
∵BD∶DC=CE∶AE=2∶1,
如图,在△ABC中,若 = = ,AD和BE交于F,则 = .
例6
∴ = =2,
∴EH= CE.
∴AE= = ,
∴ = = .
随堂练习
1.如图,已知AD∥BE∥CF,且AB∶BC=2∶1,则DF∶EF等于( )
B
A.2∶1 B.3∶1
C.4∶1 D.3∶2
2.如图,△ABC中,DE∥BC,AD=3k,BD=3k,那么DE∶BC=______.
1∶2
3.如图,已知l1∥l2∥l3,AB=3,DE=2,EF=4,则BC=_______.
6
随堂练习
随堂练习
4.在△ABC中,ED//AB,若 = ,则
=
——
——
=
5. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm,
AF = 4 cm,求菱形的边长.
解:∵ 四边形 ABCD 为菱形,
B
C
A
D
E
F
∴CD∥AB,
设菱形的边长为 x cm,则CD = AD = x cm,DF = (4-x) cm,
∴ = ,
∴ = 解得 x =
∴菱形的边长为 cm.
随堂练习
基本事实
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行线分线段成比例
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
第二十二章 相似形
22.1 比例线段
第3课时 平行线分线段成比例定理及其推论
旧知回顾
1.什么是平行线等分线段定理?
如果一组平行线在一条直线上截得的线段相等,那么它在另一条直线上截得的线段也相等.
2.求出下列各式中的x∶y.
(1)3x=5y (2)x= y (3)3∶x=5∶y
解:(1) = ;
(2) = ;
(3) =
旧知回顾
3.已知 = ,求 .
∴
=
=
,
解:∵
=
,
∴
=
,
=
∴
.
下图是一架梯子的示意图,由生活常识可以知道:
AD,BE1,CF互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
D
F
E
观察与猜想
DE=EF
什么是平行线分线段成比例定理,如何推导?
平行线分线段成比例定理推导与应用
解:如图,有一组平行线:l1∥l2∥l3…∥ln,
根据已学定理,可以得到:
如果A1A2=A2A3=…=An-1An,那么B1B2=B2B3=…Bn-1Bn.
另外,直线A1An与直线B1Bn被这一组平行线分别截于点A1,A2,…,An和点B1,B2,…,Bn.
如果设A1A2=A2A3=…An-1An=a,B1B2=B2B3=…Bn-1Bn=b,
容易得到:
=
=
,
.
所以有
=
=
=
,
符号语言
A1
A2
A3
B1
B2
B3
b
c
a
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
若a∥b∥ c ,
则 = , = ,
=
,
...
=
已知,如图,AD∥EF∥BC,BE=3,AE=9,FC=2.求DF的长.
解:∵AD∥EF∥BC,
例1
∴DF=6.
∴ = ,
∴ = ,
A
B
C
E
F
例2
如图,在△ABC中, = .
求证:(1)
=
证明:
∵
=
∴
=
∴
=
A
B
C
E
F
(2)
=
,
证明:
∵
=
,
=
.
∴
∴
=
.
=
∴
.
∴
=
.
证明:∵l1∥l2∥l3,
如图,已知l1∥l2∥l3, = ,求证 = .
例3
∴
=
=
,
∴
=
∴
=
,
∴
=
,
=
,
∴
平行线分线段成比例定理推论是什么?有哪些形式?如何证明?
平行于三角形一边的直线截其他两边(或两边延长线)所对的对应线段成比例,有三种形式,补齐图中第三条平行线可证.
平行线分线段成比例定理推论与应用
推论
如图,AD∥EG∥BC,AD=6,BC=9,AE∶AB=2∶3,求GF的长.
例4
∴ = ,
EG=6.
∵EF∥AD,
∴ = ,EF=2,
∴GF=EG-EF=6-2=4.
∵EG∥BC,
解:
证明:∵DE∥BC,
如图,△ABC中,DE∥BC,DF∥BE,求证 = .
例5
∴ = .
∵DF∥BE,
∴ = ,
∴ = .
解:过D作DH∥BE交AC于H.
∵BD∶DC=CE∶AE=2∶1,
如图,在△ABC中,若 = = ,AD和BE交于F,则 = .
例6
∴ = =2,
∴EH= CE.
∴AE= = ,
∴ = = .
随堂练习
1.如图,已知AD∥BE∥CF,且AB∶BC=2∶1,则DF∶EF等于( )
B
A.2∶1 B.3∶1
C.4∶1 D.3∶2
2.如图,△ABC中,DE∥BC,AD=3k,BD=3k,那么DE∶BC=______.
1∶2
3.如图,已知l1∥l2∥l3,AB=3,DE=2,EF=4,则BC=_______.
6
随堂练习
随堂练习
4.在△ABC中,ED//AB,若 = ,则
=
——
——
=
5. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm,
AF = 4 cm,求菱形的边长.
解:∵ 四边形 ABCD 为菱形,
B
C
A
D
E
F
∴CD∥AB,
设菱形的边长为 x cm,则CD = AD = x cm,DF = (4-x) cm,
∴ = ,
∴ = 解得 x =
∴菱形的边长为 cm.
随堂练习
基本事实
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行线分线段成比例
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
