沪科版九年级数学上册 22.1.2 比例的基本性质与黄金分割 课件(共38张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 22.1.2 比例的基本性质与黄金分割 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:46:06 | ||
图片预览










文档简介
(共38张PPT)
第二十二章 相似形
22.1 比例线段
第2课时 比例的基本性质与黄金分割
什么叫两个数的比?2与-3的比,-4与6的比,如何表示?其比值相等吗?用小学学过的方法可说成什么?可写成什么形式?
旧知回顾
=- , = ,比值相等,
两个数相除的商也叫两个数的比. =- ,
写成2∶-3=-4∶6.
可以说2,-3,-4,6成比例,
导入新课
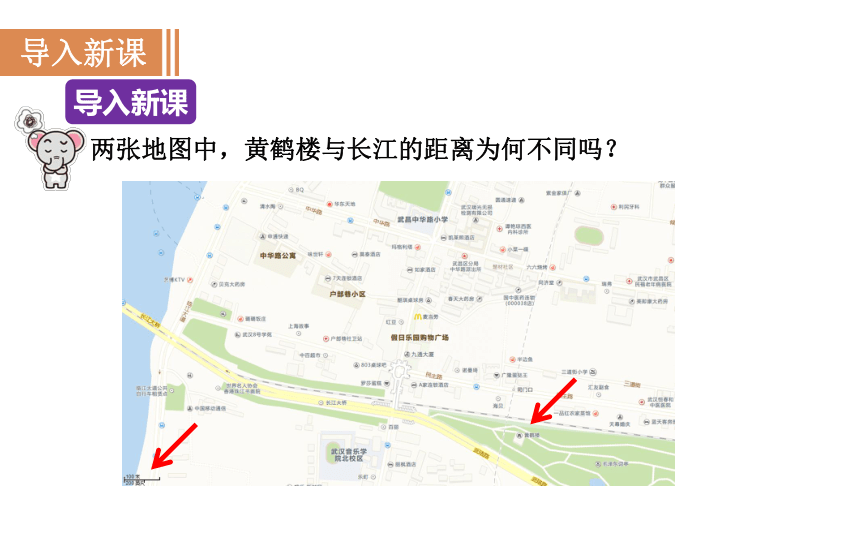
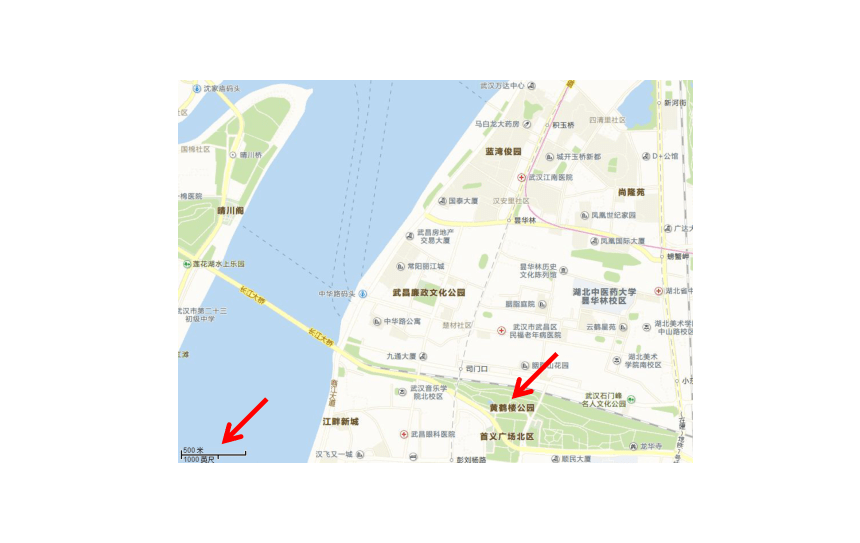
两张地图中,黄鹤楼与长江的距离为何不同吗?
如果选用同一个长度单位得两条先线段AB,CD的长度分别是m , n,那么这两条线段的比就是它们长度的比,即
A
B
C
D
m
n
AB:CD= m : n 或
如果把 表示成比值k,那么 =k,或AB=k · CD,两条线段的比实际上就是两个数的比.
一 比例线段的基本概念
什么叫两条线段的比?
归纳
两条线段长度的比叫两条线段的比,记作 或a∶b,
什么叫成比例线段?
在四条线段a、b、c、d中,如果其中两条线段a、b的比等于另外两条线段c、d的比,即 = (或a∶b=c∶d),那么这四条线段叫做成比例线段.简称比例线段.
什么是比例中项?
其中a,d叫做比例外项,b,c叫做比例内项.如果作为比例内项的两条线段是相等的,即线段a、b、c之间有a∶b=b∶c,那么线段b叫做线段a、c的比例中项.
判断下列线段a、b、c、d是否是成比例线
(1)a=4,b=6,c=5,d=10;
∴ 线段a、b、c、d 不是成比例线段.
解:(1)∵
=
=
=
=
∴
≠
例1
(2)a=2,b=
,c=
,d=
.
∴ 线段a、b、c、d是成比例线段.
∴
=
=
=
,
=
=
解 ∵
注意
若a:b=k , 说明a是b的 k 倍;
两条线段的比与所采用的长度单位无关,但求比时两条线段的长度单位必须一致;
两条线段的比值是一个没有单位的正数;
除了a=b外,a:b≠b:a, 与 ,互为倒数.
如图的(1)和(2)都是故宫太和殿的照片,(2)是由(1)缩小得到的.
(1)
(2)
P
Q
P′
Q′
A
A'
B'
B
观察与思考
在照片(1)中任意取四个点P,Q,A ,B在照片(2)找出对应的两个点P′,Q′,A′, B′量出线段PQ,P′Q′,AB, A′B′的长度.计算它们的长度的比值.
二 比例的基本性质及合比、等比性质
问题:如果四个数a , b, c, d成比例,即 = 那么ad = bc吗?反过来如果ad = bc,那么a , b, c , d四个数成比例吗?
如果四个数a,b,c,d成比例,即 = 那么ad=bc吗?
1
由此可得到比例的基本性质:
如果 = ,那么 ad=bc.
在等式两边同时乘以bd,得ad=bc
比例的基本性质
2
由此可得到比例的基本性质:
如果ad=bc,那么等式 = 还成立吗?
在等式中,四个数a,b,c,d可以为任意数,而在分式中,分母不能为0.
如果ad=bc(a,b,c,d都不等于0),那么 = .
根据下列条件,求 a : b 的值:
(1) 4a=5b ;
解(1)∵ 4a=5b,
(2)
=
∴
=
(2)∵ = ,
∴
=
例2
已知 = ,求 的值
解:解法1:由比例的基本性质,
得 2(a+3b)=7×2b.
∴a=4b,∴ =4
解法2:由 = ,得 =7
∴
= +3=7,
∴ =4
例3
什么是合比性质?
解:如果 = ,
得 = (b、d≠0),
合比性质
在 = 两边加上1,
由此可得到比例的合比性质
得 = ;
如果 = ,
等比性质
已知a , b, c, d, e, f 六个数,如果 = =
(b+d+f≠0),那么 成立吗?为什么?
解设 = = = k ,
则 a = kb, c = kd , e= kf .
所以 = = k =
由此可得到比例的又一性质:
归纳
如果 = =....= (b+d+...+n≠0)
那么 =
在△ABC与△DEF中,已知 ,且△ABC的周长为18cm,求△DEF得周长.
解:∵
∴
∴4(AB + BC + CA)=3(DE + EF + FD).
又 △ABC的周长为18cm,
即 AB+BC+CA=18cm.
∴ △DEF的周长为24cm.
即 AB+BC+CA = (DE+EF+FD) ,
例4
在地图或工程图纸上,都标有比例尺,比例尺就是图上距离与实际距离的比,现在一长比例尺为1∶5000的图纸上,量得一个△ABC的三边:AC=3cm,BC=4cm,AB=5cm,这个图纸所反映的实际△A’B’C’的周长是多少?
解:根据题意,得
即
∵ AB+BC+AC=5+4+3=12(cm),
例5
答:实际△A'B'C'的周长是600m
∴ A'B'+B'C'+A'C'=12×5000=60000(cm)=600(m).
A
C
B
A
B
C
一个五角星如下图所示.
问题:度量C到点A、B的距离, 与 相等吗?
=
三 黄金分割
A
B
C
点C把线段AB分成两条线段AC和BC,如果 = , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点, AC与AB的比称为黄金比.
A
P
B
解 设AP=x,那么PB=a-x.根据题意,得 a:x=x:(a-x),
如图,已知线段AB的长度为a,点P是AB上一点,且使 AB:AP=AP:PB,求线段AB的长和 的值.
即 x2+ax-a2=0.
解方程,得
例6
A
P
B
因为线段长不能是负值,所以取
即
AP=
于是 = = ≈0.618.
通过上面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
知识拓展
黄 金 分 割 在 艺术 上 的 应 用
知识拓展
打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人
联想起许多与北纬30度有关的地方。
奇石异峰,名川秀水的黄山,庐山,
九寨沟等等。衔远山,吞长江的中国
三大淡水湖也恰好在这黄金分割的纬度上。
大自然与黄金分割
知识拓展
蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618;
知识拓展
人与黄金分割
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618).这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节.上肢与下肢长度之比均近似0.618.
知识拓展
随堂练习
1.判断下列各组线段是否成比例线段,为什么?
成比例线段
不成比例线段
2.下列各组线段中成比例线段的是 ( )
C
(1)a=4,b=2,c=5,d=10
(2)a=3,b=2,c=8,d=6
A. a= ,b=3,c=2,d=
B. a=4,b=6,c=5,d=10
D. a=2,b=3,c=4,d=1
D. a=2,b= ,c= 2 ,d=
3.如果线段a=32cm,b=8cm,那么a和b的比例中项是( )
A.20cm B.18cm C.16cm D.14cm
C
解: 设比例中项为c,
由比例中项定义得:a∶c=c∶d,
c2=ab=32×8,c=16,选C.
随堂练习
随堂练习
14
4.(1)若 = ,则 =_____ ;
(2)已知 = ,则 =______.
5.已知 = = ,且3a-2b+c=9,则2a+4b-3c=________.
随堂练习
6.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为( )
A.12.36cm B.13.6cm
C.32.9cm
D.7.54cm
A
随堂练习
7.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20 cm,则它的宽约为( )
(A)12.36 cm (B)13.6 cm
(C)32.36 cm (D)7.64 cm
A
【解析】选A. 0.618×20=12.36(cm).
随堂练习
8. 如图:在△ABC中,AB=AC, ∠BAC=36°, BD平分∠ABC交AC于点D, 求证:D是AC的黄金分割点.
证明:在等腰△ABC中,顶角∠A=36°,
所以∠ABC=∠C=72°,
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°,
在△ACB和△BCD中,∠BDC=72°
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD,
∴AC:BC=BC:DC;
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°,
∴BD=BC,
∴AD=BC,
∴AC:AD=AD:DC;
即点D是AC的黄金分割点.
∵∠A=∠ABD,
∴AD=BD.
随堂练习
比例线段
两条线段的比:
比例线段
①长度单位统一;
②与单位无关,本身没有单位;
③两条线段有顺序要求.
①概念:项、比例内项、比例外项;
②四条线段有顺序要求;
③特别地:比例中项.
=
定 义
黄金分割
点C把线段AB分成两条线段AC和BC,如果 = , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
一条线段有两个黄金分割点
黄金比:较长线段:
原线段 =
第二十二章 相似形
22.1 比例线段
第2课时 比例的基本性质与黄金分割
什么叫两个数的比?2与-3的比,-4与6的比,如何表示?其比值相等吗?用小学学过的方法可说成什么?可写成什么形式?
旧知回顾
=- , = ,比值相等,
两个数相除的商也叫两个数的比. =- ,
写成2∶-3=-4∶6.
可以说2,-3,-4,6成比例,
导入新课
两张地图中,黄鹤楼与长江的距离为何不同吗?
如果选用同一个长度单位得两条先线段AB,CD的长度分别是m , n,那么这两条线段的比就是它们长度的比,即
A
B
C
D
m
n
AB:CD= m : n 或
如果把 表示成比值k,那么 =k,或AB=k · CD,两条线段的比实际上就是两个数的比.
一 比例线段的基本概念
什么叫两条线段的比?
归纳
两条线段长度的比叫两条线段的比,记作 或a∶b,
什么叫成比例线段?
在四条线段a、b、c、d中,如果其中两条线段a、b的比等于另外两条线段c、d的比,即 = (或a∶b=c∶d),那么这四条线段叫做成比例线段.简称比例线段.
什么是比例中项?
其中a,d叫做比例外项,b,c叫做比例内项.如果作为比例内项的两条线段是相等的,即线段a、b、c之间有a∶b=b∶c,那么线段b叫做线段a、c的比例中项.
判断下列线段a、b、c、d是否是成比例线
(1)a=4,b=6,c=5,d=10;
∴ 线段a、b、c、d 不是成比例线段.
解:(1)∵
=
=
=
=
∴
≠
例1
(2)a=2,b=
,c=
,d=
.
∴ 线段a、b、c、d是成比例线段.
∴
=
=
=
,
=
=
解 ∵
注意
若a:b=k , 说明a是b的 k 倍;
两条线段的比与所采用的长度单位无关,但求比时两条线段的长度单位必须一致;
两条线段的比值是一个没有单位的正数;
除了a=b外,a:b≠b:a, 与 ,互为倒数.
如图的(1)和(2)都是故宫太和殿的照片,(2)是由(1)缩小得到的.
(1)
(2)
P
Q
P′
Q′
A
A'
B'
B
观察与思考
在照片(1)中任意取四个点P,Q,A ,B在照片(2)找出对应的两个点P′,Q′,A′, B′量出线段PQ,P′Q′,AB, A′B′的长度.计算它们的长度的比值.
二 比例的基本性质及合比、等比性质
问题:如果四个数a , b, c, d成比例,即 = 那么ad = bc吗?反过来如果ad = bc,那么a , b, c , d四个数成比例吗?
如果四个数a,b,c,d成比例,即 = 那么ad=bc吗?
1
由此可得到比例的基本性质:
如果 = ,那么 ad=bc.
在等式两边同时乘以bd,得ad=bc
比例的基本性质
2
由此可得到比例的基本性质:
如果ad=bc,那么等式 = 还成立吗?
在等式中,四个数a,b,c,d可以为任意数,而在分式中,分母不能为0.
如果ad=bc(a,b,c,d都不等于0),那么 = .
根据下列条件,求 a : b 的值:
(1) 4a=5b ;
解(1)∵ 4a=5b,
(2)
=
∴
=
(2)∵ = ,
∴
=
例2
已知 = ,求 的值
解:解法1:由比例的基本性质,
得 2(a+3b)=7×2b.
∴a=4b,∴ =4
解法2:由 = ,得 =7
∴
= +3=7,
∴ =4
例3
什么是合比性质?
解:如果 = ,
得 = (b、d≠0),
合比性质
在 = 两边加上1,
由此可得到比例的合比性质
得 = ;
如果 = ,
等比性质
已知a , b, c, d, e, f 六个数,如果 = =
(b+d+f≠0),那么 成立吗?为什么?
解设 = = = k ,
则 a = kb, c = kd , e= kf .
所以 = = k =
由此可得到比例的又一性质:
归纳
如果 = =....= (b+d+...+n≠0)
那么 =
在△ABC与△DEF中,已知 ,且△ABC的周长为18cm,求△DEF得周长.
解:∵
∴
∴4(AB + BC + CA)=3(DE + EF + FD).
又 △ABC的周长为18cm,
即 AB+BC+CA=18cm.
∴ △DEF的周长为24cm.
即 AB+BC+CA = (DE+EF+FD) ,
例4
在地图或工程图纸上,都标有比例尺,比例尺就是图上距离与实际距离的比,现在一长比例尺为1∶5000的图纸上,量得一个△ABC的三边:AC=3cm,BC=4cm,AB=5cm,这个图纸所反映的实际△A’B’C’的周长是多少?
解:根据题意,得
即
∵ AB+BC+AC=5+4+3=12(cm),
例5
答:实际△A'B'C'的周长是600m
∴ A'B'+B'C'+A'C'=12×5000=60000(cm)=600(m).
A
C
B
A
B
C
一个五角星如下图所示.
问题:度量C到点A、B的距离, 与 相等吗?
=
三 黄金分割
A
B
C
点C把线段AB分成两条线段AC和BC,如果 = , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点, AC与AB的比称为黄金比.
A
P
B
解 设AP=x,那么PB=a-x.根据题意,得 a:x=x:(a-x),
如图,已知线段AB的长度为a,点P是AB上一点,且使 AB:AP=AP:PB,求线段AB的长和 的值.
即 x2+ax-a2=0.
解方程,得
例6
A
P
B
因为线段长不能是负值,所以取
即
AP=
于是 = = ≈0.618.
通过上面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
知识拓展
黄 金 分 割 在 艺术 上 的 应 用
知识拓展
打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人
联想起许多与北纬30度有关的地方。
奇石异峰,名川秀水的黄山,庐山,
九寨沟等等。衔远山,吞长江的中国
三大淡水湖也恰好在这黄金分割的纬度上。
大自然与黄金分割
知识拓展
蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618;
知识拓展
人与黄金分割
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618).这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节.上肢与下肢长度之比均近似0.618.
知识拓展
随堂练习
1.判断下列各组线段是否成比例线段,为什么?
成比例线段
不成比例线段
2.下列各组线段中成比例线段的是 ( )
C
(1)a=4,b=2,c=5,d=10
(2)a=3,b=2,c=8,d=6
A. a= ,b=3,c=2,d=
B. a=4,b=6,c=5,d=10
D. a=2,b=3,c=4,d=1
D. a=2,b= ,c= 2 ,d=
3.如果线段a=32cm,b=8cm,那么a和b的比例中项是( )
A.20cm B.18cm C.16cm D.14cm
C
解: 设比例中项为c,
由比例中项定义得:a∶c=c∶d,
c2=ab=32×8,c=16,选C.
随堂练习
随堂练习
14
4.(1)若 = ,则 =_____ ;
(2)已知 = ,则 =______.
5.已知 = = ,且3a-2b+c=9,则2a+4b-3c=________.
随堂练习
6.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为( )
A.12.36cm B.13.6cm
C.32.9cm
D.7.54cm
A
随堂练习
7.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20 cm,则它的宽约为( )
(A)12.36 cm (B)13.6 cm
(C)32.36 cm (D)7.64 cm
A
【解析】选A. 0.618×20=12.36(cm).
随堂练习
8. 如图:在△ABC中,AB=AC, ∠BAC=36°, BD平分∠ABC交AC于点D, 求证:D是AC的黄金分割点.
证明:在等腰△ABC中,顶角∠A=36°,
所以∠ABC=∠C=72°,
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°,
在△ACB和△BCD中,∠BDC=72°
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD,
∴AC:BC=BC:DC;
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°,
∴BD=BC,
∴AD=BC,
∴AC:AD=AD:DC;
即点D是AC的黄金分割点.
∵∠A=∠ABD,
∴AD=BD.
随堂练习
比例线段
两条线段的比:
比例线段
①长度单位统一;
②与单位无关,本身没有单位;
③两条线段有顺序要求.
①概念:项、比例内项、比例外项;
②四条线段有顺序要求;
③特别地:比例中项.
=
定 义
黄金分割
点C把线段AB分成两条线段AC和BC,如果 = , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
一条线段有两个黄金分割点
黄金比:较长线段:
原线段 =
