沪科版九年级数学上册22.3.1 相似三角形的性质 课件 (共21张PPT)
文档属性
| 名称 | 沪科版九年级数学上册22.3.1 相似三角形的性质 课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:34:22 | ||
图片预览






文档简介
(共21张PPT)
第二十二章 相似形
22.3 相似三角形的性质
第1课时 相似三角形的性质
旧知回顾
1.什么叫相似三角形?相似比指的是什么?
2.全等三角形是相似三角形吗?全等三角形的相似比是多少?
3.相似三角形的判定方法有哪些?
对应边成比例,对应角相等的两个三角形叫相似三角形,对应边的比也叫相似比.
全等三角形是相似三角形,其相似比为1.
共五种,略.
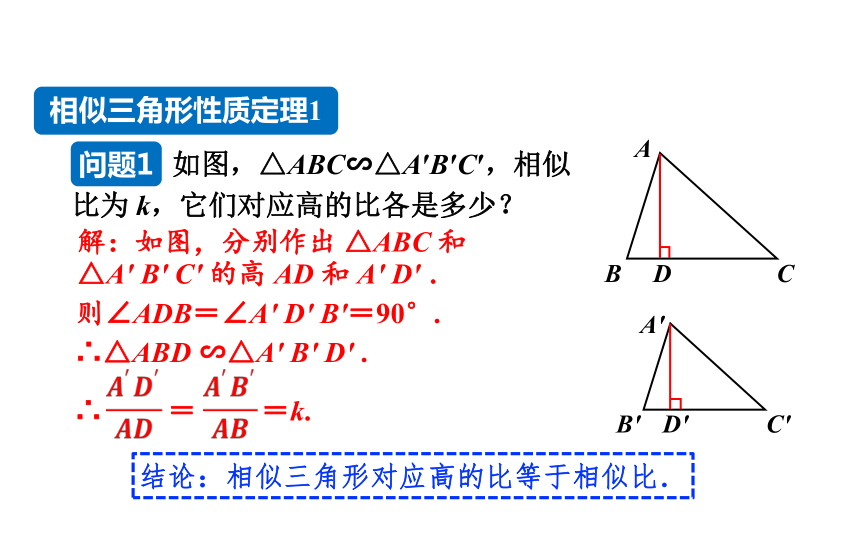
如图,△ABC∽△A′B′C′,相似比为 k,它们对应高的比各是多少?
相似三角形性质定理1
问题1
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A' D' .
则∠ADB=∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A'
B'
C'
D'
A
B
C
D
结论:相似三角形对应高的比等于相似比.
∴ = =k.
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
问题2
把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
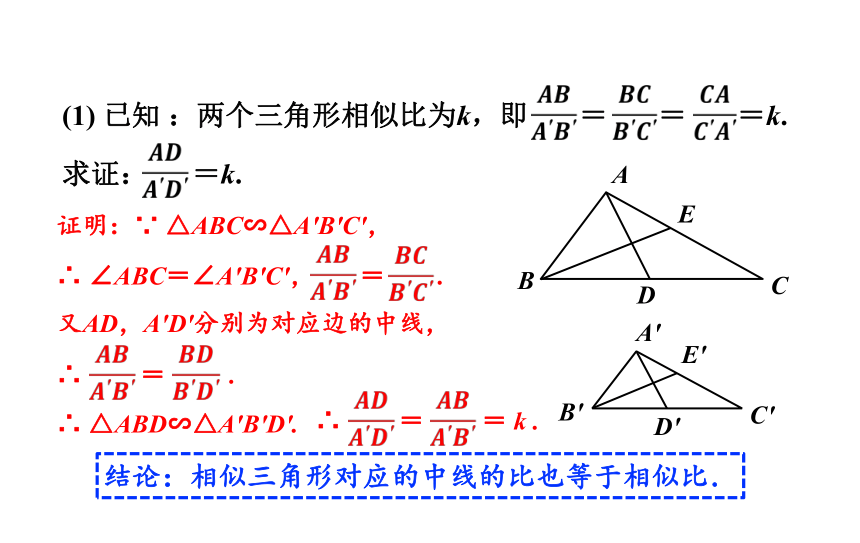
结论:相似三角形对应的中线的比也等于相似比.
(1) 已知 :两个三角形相似比为k,即 = = =k.
求证: =k.
证明:∵ △ABC∽△A′B′C′,
∴ ∠ABC=∠A′B′C′, = .
又AD,A′D′分别为对应边的中线,
∴ = .
∴ △ABD∽△A′B′D′.
A
B
C
D
E
A'
B'
D'
C'
E'
∴ = = k .
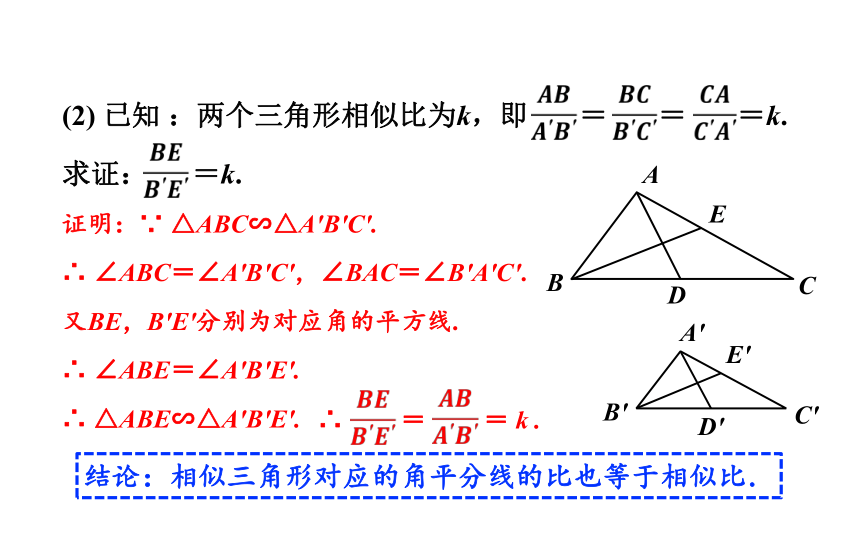
结论:相似三角形对应的角平分线的比也等于相似比.
(2) 已知 :两个三角形相似比为k,即 = = =k.
求证: =k.
证明:∵ △ABC∽△A′B′C′.
∴ ∠ABC=∠A′B′C′,∠BAC=∠B′A′C′.
又BE,B′E′分别为对应角的平方线.
∴ △ABE∽△A′B′E′.
A
B
C
D
E
A'
B'
D'
C'
E'
∴ ∠ABE=∠A′B′E′.
∴ = = k .
相似三角形性质定理1
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
图中①②③分别是边长为1,2,3的等边三角形,它们都相似吗?
①
1
②
2
③
3
①与②的相似比=______,①与②的周长比=______;
①与③的相似比=______,①与③的周长比=______.
1 : 2
都相似
相似三角形性质定理2和定理3
问题3
1 : 2
1 : 3
1 : 3
结论: 相似三角形的周长比等于相似比.
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
思考:怎么证明这一结论呢?
相似三角形性质定理2
相似三角形周长的比等于相似比.
①与②的相似比=______,①与②的面积比=______;
①与③的相似比=______,①与③的面积比=______.
1 : 2
1 : 4
1 : 3
1 : 9
图中①②③分别是边长为1、2、3的等边三角形,回答以下问题:
问题4
结论: 相似三角形的面积比等于相似比的平方.
①
1
②
2
③
3
求证:相似三角形的面积比等于相似比的平方.
思考:怎么证明这一结论呢?
A'
B'
C'
A
B
C
证明:设△ABC∽△A′B′C′,相似比为k,
如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′,
∵△ABC∽△A′B′C′,
∴ = ,
∴ = ,
∴ = k,
∴ = = · =k·k=k2 .
D
D'
相似三角形性质定理3
相似三角形的面积比等于相似比的平方.
两个相似三角形的两条对应边的长分别是6 cm和8 cm,如果它们对应的两条角平分线的和为42 cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为x cm,
解得x=18.
较长的角平分线长为24 cm.
故这两条角平分线的长分别为18 cm,24 cm.
则由相似性质有 = .
例1
∴△DEF∽△ABC,相似比为1 : 2,
∴△DEF的周长= △ABC的周长,
△DEF的周长为12.
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,求△DEF的周长.
A
B
C
D
E
F
又∠D=∠A,
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
例2
∴ = = .
∴ △ADE∽△ABC.
解 ∵ DE//BC,
A
B
C
D
E
如图,△ABC的面积为25,直线 DE//BC,如果 △ADE的面积为9,求 的值.
∴ = = .
∴ = .
∴ = .
例3
随堂练习
1.如图,在△ABC中,DE∥BC,AH是△ABC的角平分线,交DE于点G. DE : BC=2 : 3,那么AG : GH=________.
2.在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为________.
A
B
C
D
E
G
H
2 : 1
8,3
3.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的 倍,那么边长应缩短到原来的_______.
解:∵△ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2 cm.
A
G
B
C
D
E
F
H
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
∴ = ,
∴ = ,
5.若△ABC∽△A′B′C′ ,它们的周长分别为60 cm和72 cm,且AB=15 cm,B′C′=24 cm,求BC,AC,A′B′,A′C′的长.
B
A
C
解:∵△ABC∽△A′B′C′ ,它们的周长分别为60 cm和72 cm,
∵AB=15 cm,B′C′=24 cm,
∴BC=20 cm, AC=25 cm,
A′B′=18 cm,A′C′=30 cm.
∴ = = = ,
B′
A′
C′
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36=64 (cm2).
B
C
A
D
E
6.如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 = = ,求四边形 BCDE 的面积.
解:∵∠BAC=∠DAE,且 = = ,
定理1
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
定理2
定理3
相似三角形的性质
相似三角形周长的比等于相似比.
相似三角形的面积比等于相似比的平方.
第二十二章 相似形
22.3 相似三角形的性质
第1课时 相似三角形的性质
旧知回顾
1.什么叫相似三角形?相似比指的是什么?
2.全等三角形是相似三角形吗?全等三角形的相似比是多少?
3.相似三角形的判定方法有哪些?
对应边成比例,对应角相等的两个三角形叫相似三角形,对应边的比也叫相似比.
全等三角形是相似三角形,其相似比为1.
共五种,略.
如图,△ABC∽△A′B′C′,相似比为 k,它们对应高的比各是多少?
相似三角形性质定理1
问题1
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A' D' .
则∠ADB=∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A'
B'
C'
D'
A
B
C
D
结论:相似三角形对应高的比等于相似比.
∴ = =k.
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
问题2
把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
结论:相似三角形对应的中线的比也等于相似比.
(1) 已知 :两个三角形相似比为k,即 = = =k.
求证: =k.
证明:∵ △ABC∽△A′B′C′,
∴ ∠ABC=∠A′B′C′, = .
又AD,A′D′分别为对应边的中线,
∴ = .
∴ △ABD∽△A′B′D′.
A
B
C
D
E
A'
B'
D'
C'
E'
∴ = = k .
结论:相似三角形对应的角平分线的比也等于相似比.
(2) 已知 :两个三角形相似比为k,即 = = =k.
求证: =k.
证明:∵ △ABC∽△A′B′C′.
∴ ∠ABC=∠A′B′C′,∠BAC=∠B′A′C′.
又BE,B′E′分别为对应角的平方线.
∴ △ABE∽△A′B′E′.
A
B
C
D
E
A'
B'
D'
C'
E'
∴ ∠ABE=∠A′B′E′.
∴ = = k .
相似三角形性质定理1
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
图中①②③分别是边长为1,2,3的等边三角形,它们都相似吗?
①
1
②
2
③
3
①与②的相似比=______,①与②的周长比=______;
①与③的相似比=______,①与③的周长比=______.
1 : 2
都相似
相似三角形性质定理2和定理3
问题3
1 : 2
1 : 3
1 : 3
结论: 相似三角形的周长比等于相似比.
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
思考:怎么证明这一结论呢?
相似三角形性质定理2
相似三角形周长的比等于相似比.
①与②的相似比=______,①与②的面积比=______;
①与③的相似比=______,①与③的面积比=______.
1 : 2
1 : 4
1 : 3
1 : 9
图中①②③分别是边长为1、2、3的等边三角形,回答以下问题:
问题4
结论: 相似三角形的面积比等于相似比的平方.
①
1
②
2
③
3
求证:相似三角形的面积比等于相似比的平方.
思考:怎么证明这一结论呢?
A'
B'
C'
A
B
C
证明:设△ABC∽△A′B′C′,相似比为k,
如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′,
∵△ABC∽△A′B′C′,
∴ = ,
∴ = ,
∴ = k,
∴ = = · =k·k=k2 .
D
D'
相似三角形性质定理3
相似三角形的面积比等于相似比的平方.
两个相似三角形的两条对应边的长分别是6 cm和8 cm,如果它们对应的两条角平分线的和为42 cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为x cm,
解得x=18.
较长的角平分线长为24 cm.
故这两条角平分线的长分别为18 cm,24 cm.
则由相似性质有 = .
例1
∴△DEF∽△ABC,相似比为1 : 2,
∴△DEF的周长= △ABC的周长,
△DEF的周长为12.
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,求△DEF的周长.
A
B
C
D
E
F
又∠D=∠A,
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
例2
∴ = = .
∴ △ADE∽△ABC.
解 ∵ DE//BC,
A
B
C
D
E
如图,△ABC的面积为25,直线 DE//BC,如果 △ADE的面积为9,求 的值.
∴ = = .
∴ = .
∴ = .
例3
随堂练习
1.如图,在△ABC中,DE∥BC,AH是△ABC的角平分线,交DE于点G. DE : BC=2 : 3,那么AG : GH=________.
2.在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为________.
A
B
C
D
E
G
H
2 : 1
8,3
3.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的 倍,那么边长应缩短到原来的_______.
解:∵△ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2 cm.
A
G
B
C
D
E
F
H
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
∴ = ,
∴ = ,
5.若△ABC∽△A′B′C′ ,它们的周长分别为60 cm和72 cm,且AB=15 cm,B′C′=24 cm,求BC,AC,A′B′,A′C′的长.
B
A
C
解:∵△ABC∽△A′B′C′ ,它们的周长分别为60 cm和72 cm,
∵AB=15 cm,B′C′=24 cm,
∴BC=20 cm, AC=25 cm,
A′B′=18 cm,A′C′=30 cm.
∴ = = = ,
B′
A′
C′
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36=64 (cm2).
B
C
A
D
E
6.如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 = = ,求四边形 BCDE 的面积.
解:∵∠BAC=∠DAE,且 = = ,
定理1
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
定理2
定理3
相似三角形的性质
相似三角形周长的比等于相似比.
相似三角形的面积比等于相似比的平方.
