沪科版九年级数学上册 22.3.2 相似三角形性质的应用 课件(共19张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 22.3.2 相似三角形性质的应用 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 700.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:34:51 | ||
图片预览



文档简介
(共19张PPT)
第二十二章 相似形
22.3 相似三角形的性质
第2课时 相似三角形性质的应用
旧知回顾
我们已经学习的相似三角形的性质有哪些?
相似三角形对应角相等;
相似三角形对应边成比例;
相似三角形对应边上的高线之比、对应边上中线之比、
对应角平分线之比等于相似比;
相似三角形的周长之比等于相似比;
相似三角形的面积之比等于相似比的平方.
相似三角形性质的应用举例
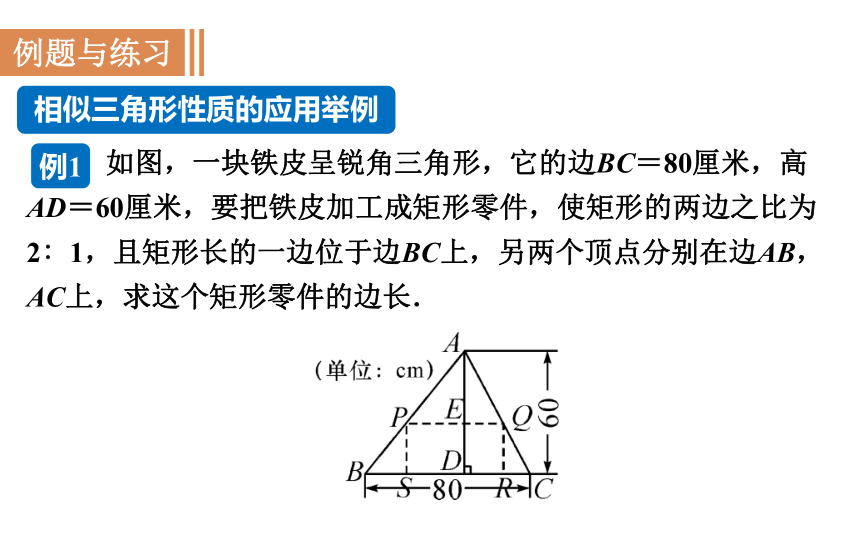
如图,一块铁皮呈锐角三角形,它的边BC=80厘米,高AD=60厘米,要把铁皮加工成矩形零件,使矩形的两边之比为2∶1,且矩形长的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的边长.
例1
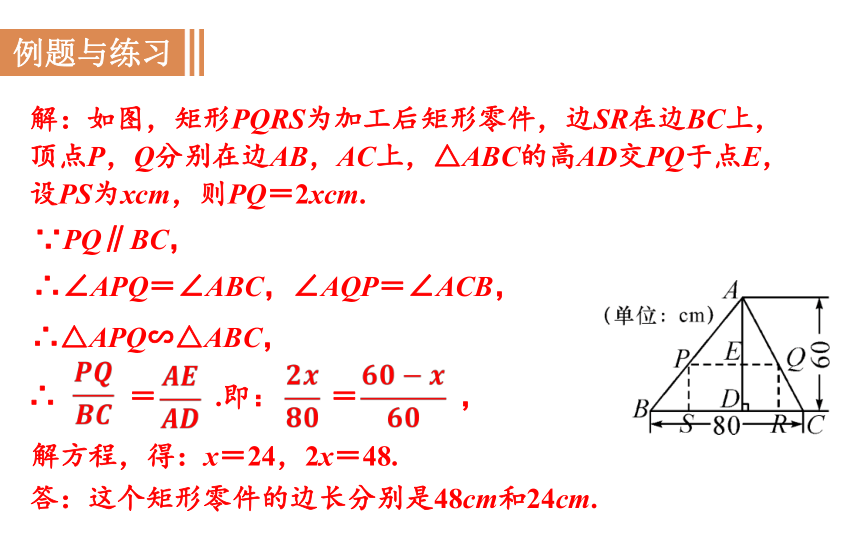
解:如图,矩形PQRS为加工后矩形零件,边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E,设PS为xcm,则PQ=2xcm.
答:这个矩形零件的边长分别是48cm和24cm.
∵PQ∥BC,
∴∠APQ=∠ABC,∠AQP=∠ACB,
∴△APQ∽△ABC,
解方程,得:x=24,2x=48.
∴ = .即: = ,
如图,△ABC是一块锐角三角形材料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
解:设正方形PQMN是符合要求的.△ABC的高AD与PN相交于点E.设正方形PQMN的边长为x毫米.
答:这个正方形零件的边长是48毫米.
练一练
∵PN∥BC,
∴△APN∽△ABC,
∴ = ,因此 = 得x=48(毫米).
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
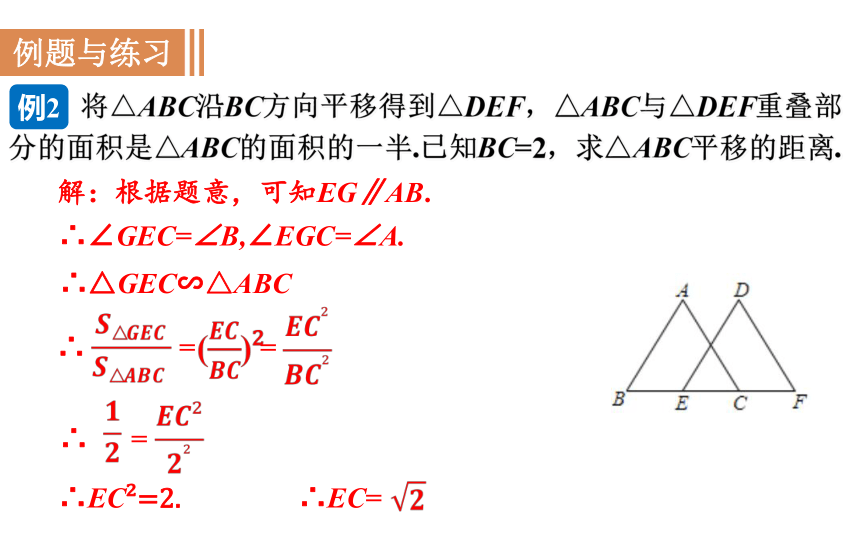
将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
例2
∴ = =
∴ =
∴EC=
∴EC =2.
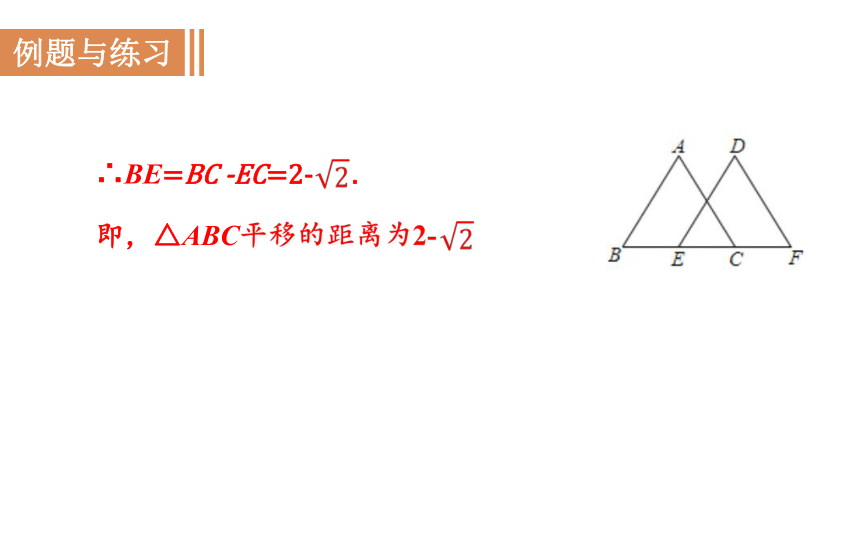
∴BE=BC -EC=2- .
即,△ABC平移的距离为2-
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
例3
∴ △ADE ∽ △ABC ,
相似比为 1 : 2,
面积比为 1 : 4.
∴ = = .
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,面积比为 1 : 4.
设 S△ABC = 4,则 S△ADE = 1,S△EFC = 1,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2,
∴ S四边形BFED : S△ABC = 2 : 4 = .
△ABC 中,DE∥BC,EF∥AB,已知 △ADE 和△EFC 的面积分别为 4 和 9,求 △ABC 的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.
练一练
∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF,
∴△ADE ∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC=2:3,则 AE : AC =2 : 5,
随堂练习
A
1.如图,在正三角形ABC中,D、E、F分别是BC、AC、AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
A. 1∶3
B. 2∶3
C. ∶2
D. ∶3
随堂练习
2.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
随堂练习
3.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则 =_________ .
4.某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上种植花木(如图所示),他们想在△AMD和△BMC地带种植单价为10元/平方米的太阳花,当△AMD地带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由.
随堂练习
∴△AMD∽△CMB.
随堂练习
∵AD=10,BC=20,
∵S△AMD=500÷10=50(平方米),
∴S△CMB=200(平方米).
因此还需要资金200×10=2000(元).
而剩余资金为2000-500=1500(元)<2000元.
∴资金不够用.
∴ =( )2=
解:∵AD∥BC,
5.如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=5cm,AD=10cm,若矩形PQRS的长是宽的2倍,你能求出这个矩形的面积吗?
S
R
Q
P
E
D
C
B
A
随堂练习
解:情况一:SR=2SP
设SP=xcm,则SR=2x cm
所以 x=2 2x=4
S矩形PQRS= 2×4=8cm2
得到: =
S
R
Q
P
E
D
C
B
A
解:情况二:SP=2SR
随堂练习
设SR=xcm,则SP=2x cm
S矩形PQRS=2.5×5=12.5cm2
所以 x=2.5 2x=5
得到: =
6.如图,这是圆桌正上方的灯泡 (点A) 发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米,
随堂练习
∴ AF = AH-FH = 2 (米),
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,
∴△ADF ∽△ACH,
A
D
E
F
C
B
H
解得 CH = 0.9米.
答:地面上阴影部分的面积为 2.54 平方米.
随堂练习
∴ 阴影部分的面积为:
∴ = ,即 = ,
πCH = π ×0.9 ≈2.54(平方米).
第二十二章 相似形
22.3 相似三角形的性质
第2课时 相似三角形性质的应用
旧知回顾
我们已经学习的相似三角形的性质有哪些?
相似三角形对应角相等;
相似三角形对应边成比例;
相似三角形对应边上的高线之比、对应边上中线之比、
对应角平分线之比等于相似比;
相似三角形的周长之比等于相似比;
相似三角形的面积之比等于相似比的平方.
相似三角形性质的应用举例
如图,一块铁皮呈锐角三角形,它的边BC=80厘米,高AD=60厘米,要把铁皮加工成矩形零件,使矩形的两边之比为2∶1,且矩形长的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的边长.
例1
解:如图,矩形PQRS为加工后矩形零件,边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E,设PS为xcm,则PQ=2xcm.
答:这个矩形零件的边长分别是48cm和24cm.
∵PQ∥BC,
∴∠APQ=∠ABC,∠AQP=∠ACB,
∴△APQ∽△ABC,
解方程,得:x=24,2x=48.
∴ = .即: = ,
如图,△ABC是一块锐角三角形材料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
解:设正方形PQMN是符合要求的.△ABC的高AD与PN相交于点E.设正方形PQMN的边长为x毫米.
答:这个正方形零件的边长是48毫米.
练一练
∵PN∥BC,
∴△APN∽△ABC,
∴ = ,因此 = 得x=48(毫米).
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
例2
∴ = =
∴ =
∴EC=
∴EC =2.
∴BE=BC -EC=2- .
即,△ABC平移的距离为2-
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
例3
∴ △ADE ∽ △ABC ,
相似比为 1 : 2,
面积比为 1 : 4.
∴ = = .
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,面积比为 1 : 4.
设 S△ABC = 4,则 S△ADE = 1,S△EFC = 1,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2,
∴ S四边形BFED : S△ABC = 2 : 4 = .
△ABC 中,DE∥BC,EF∥AB,已知 △ADE 和△EFC 的面积分别为 4 和 9,求 △ABC 的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.
练一练
∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF,
∴△ADE ∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC=2:3,则 AE : AC =2 : 5,
随堂练习
A
1.如图,在正三角形ABC中,D、E、F分别是BC、AC、AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
A. 1∶3
B. 2∶3
C. ∶2
D. ∶3
随堂练习
2.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
随堂练习
3.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则 =_________ .
4.某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上种植花木(如图所示),他们想在△AMD和△BMC地带种植单价为10元/平方米的太阳花,当△AMD地带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由.
随堂练习
∴△AMD∽△CMB.
随堂练习
∵AD=10,BC=20,
∵S△AMD=500÷10=50(平方米),
∴S△CMB=200(平方米).
因此还需要资金200×10=2000(元).
而剩余资金为2000-500=1500(元)<2000元.
∴资金不够用.
∴ =( )2=
解:∵AD∥BC,
5.如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=5cm,AD=10cm,若矩形PQRS的长是宽的2倍,你能求出这个矩形的面积吗?
S
R
Q
P
E
D
C
B
A
随堂练习
解:情况一:SR=2SP
设SP=xcm,则SR=2x cm
所以 x=2 2x=4
S矩形PQRS= 2×4=8cm2
得到: =
S
R
Q
P
E
D
C
B
A
解:情况二:SP=2SR
随堂练习
设SR=xcm,则SP=2x cm
S矩形PQRS=2.5×5=12.5cm2
所以 x=2.5 2x=5
得到: =
6.如图,这是圆桌正上方的灯泡 (点A) 发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米,
随堂练习
∴ AF = AH-FH = 2 (米),
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,
∴△ADF ∽△ACH,
A
D
E
F
C
B
H
解得 CH = 0.9米.
答:地面上阴影部分的面积为 2.54 平方米.
随堂练习
∴ 阴影部分的面积为:
∴ = ,即 = ,
πCH = π ×0.9 ≈2.54(平方米).
