沪科版九年级数学上册 23.1.1 正切 课件(共31张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 23.1.1 正切 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览





文档简介
(共31张PPT)
第二十三章 解直角三角形
23.1 锐角的三角函数
第1课时 正切
直角三角形中某个锐角的正切值;了解坡度的有关概念.
理解正切、倾斜程度、坡度的数学意义,密切数学与生活的联系.
理解正切的意义,并用它来表示两边的比.
正切
图片欣赏
思考:衡量山“险”与“不险”的标准是什么呢?
陡
陡意味着倾斜程度大
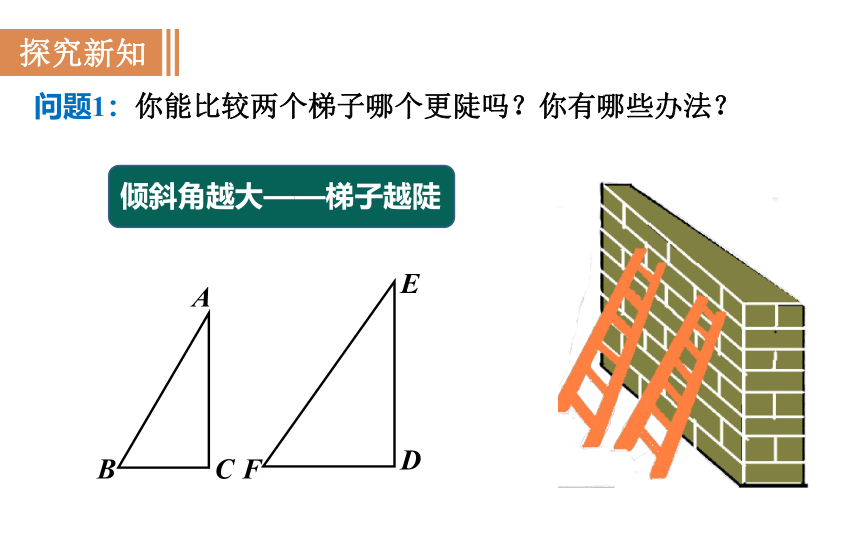
想一想:你能比较两个梯子哪个更陡吗?你有哪些办法?
A
C
B
铅直高度
水平宽度
相关概念
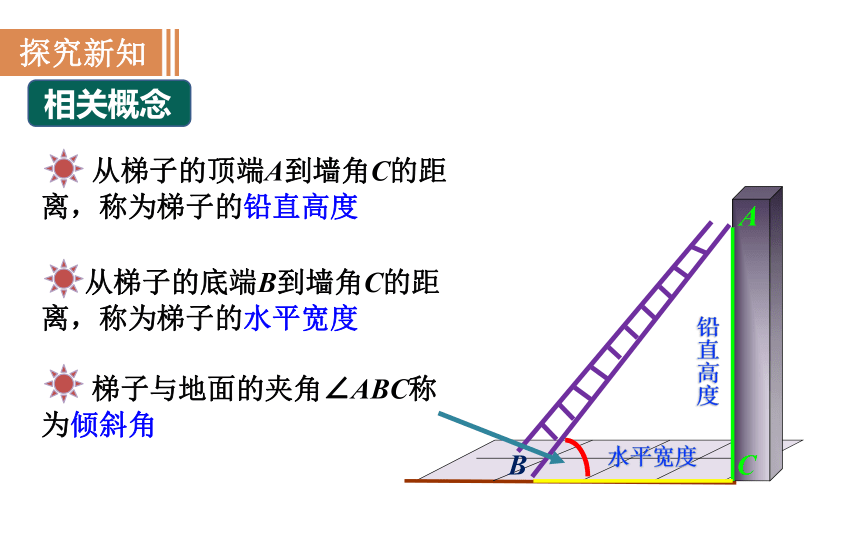
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
梯子与地面的夹角∠ABC称为倾斜角
问题1:你能比较两个梯子哪个更陡吗?你有哪些办法?
A
B
C
D
E
F
倾斜角越大——梯子越陡
4m
2m
A
B
C
4m
3m
F
E
D
问题2:如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度一样,水平宽度越小,梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
4m
2m
E
F
D
3m
2m
A
B
C
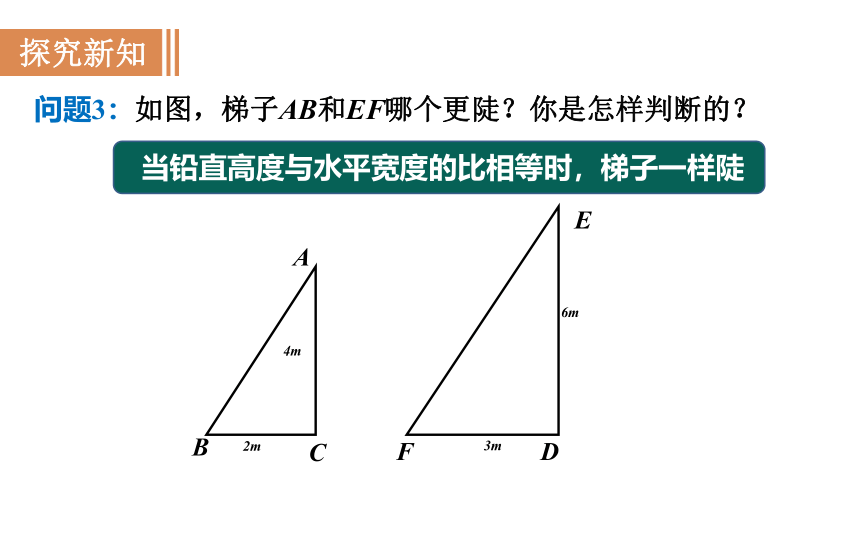
问题3:如图,梯子AB和EF哪个更陡?你是怎样判断的?
3m
6m
D
E
F
C
2m
B
4m
A
当铅直高度与水平宽度的比相等时,梯子一样陡
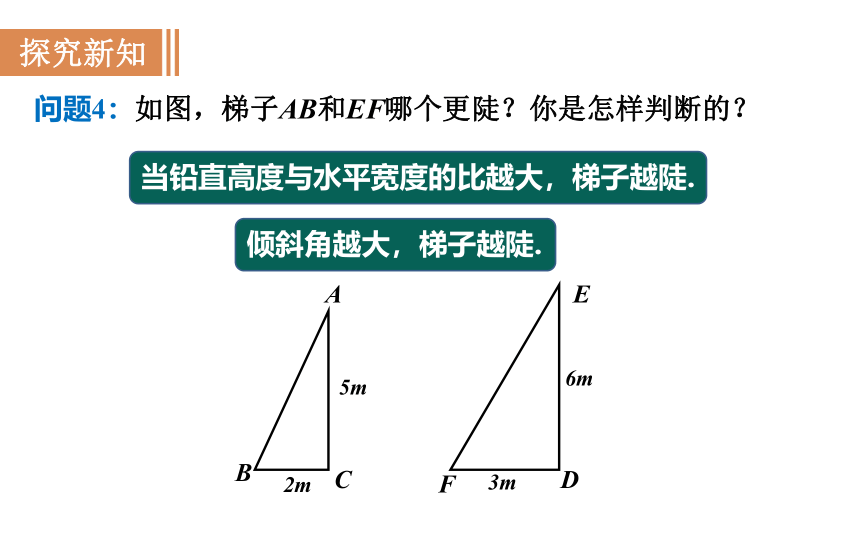
问题4:如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度与水平宽度的比越大,梯子越陡.
倾斜角越大,梯子越陡.
2m
5m
A
B
C
3m
6m
D
E
F
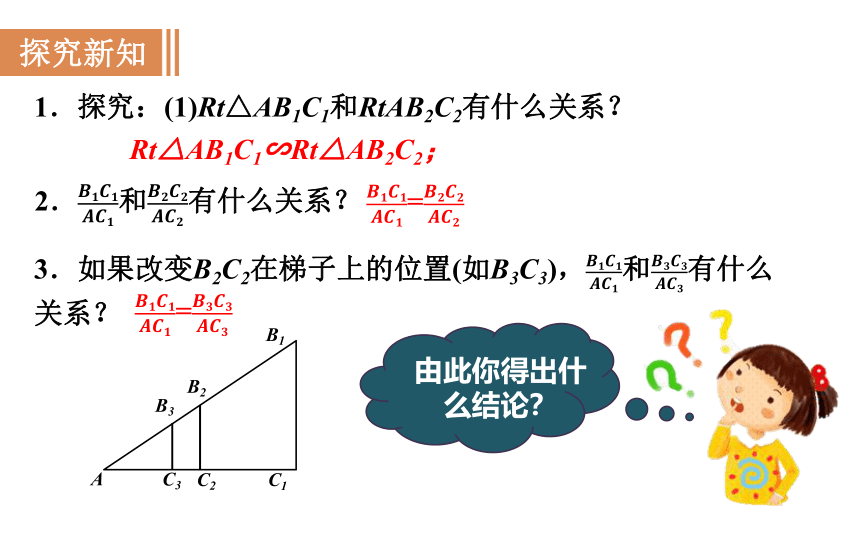
1.探究:(1)Rt△AB1C1和RtAB2C2有什么关系?
2.和有什么关系?
3.如果改变B2C2在梯子上的位置(如B3C3),和有什么关系?
B3
B2
C2
C3
A
C1
B1
Rt△AB1C1∽Rt△AB2C2;
=
=
由此你得出什么结论?
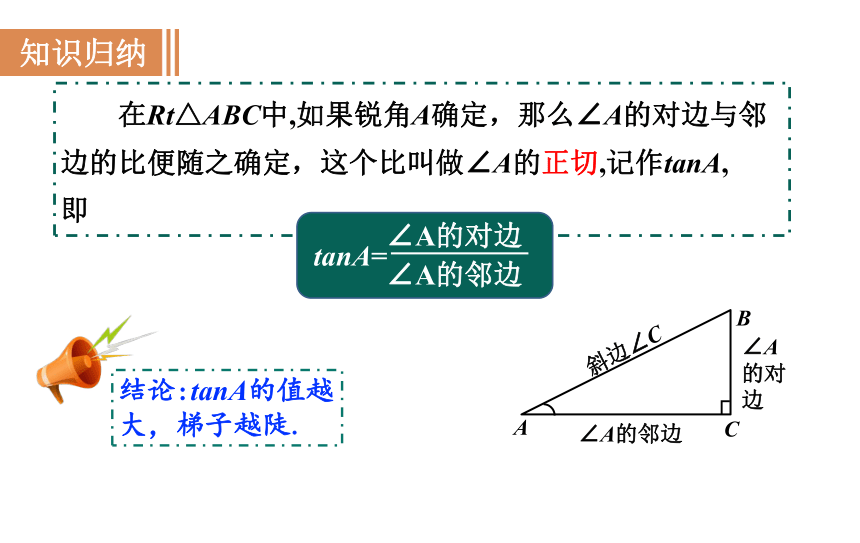
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,
即
A
B
C
∠A的对边
∠A的邻边
┌
斜边∠C
结论:tanA的值越大,梯子越陡.
tanA=
∠A的对边
∠A的邻边
4.tanA不表示“tan”乘以“A ”.
定义中的几点说明:
1.初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2.tanA是一个完整的符号,它表示∠A的正切.但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3.tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序:).
5.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
锐角A的正切值可以等于1吗?为什么?可以大于1吗?
对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.
解:可以等于1,此时为等腰直角三角形;也可以大于1,甚至可逼近于无穷大.
议一议
A
B
C
如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗?
∴CD=1.5,
解:∵△ABC是等腰直角三角形,BD⊥AC,
∴tanC===1.
1.5
A
B
C
D
3
例1
下图表示两个自动扶梯,哪一个自动扶梯比较陡
β
6m
乙
8m
α
5m
甲
13m
解:甲梯中,tanα==
乙梯中,tanβ = =
∵tanβ>tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
例2
tanB= =
( )
BC
( )
BD
tanA= =
( )
AC
( )
AD
随堂练习
1. 在Rt△ABC中,∠C=90°,AC=7,BC=5,则
tan A=_____,tanB =______.
2.下图中∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
BC
CD
AC
CD
互余两锐角的正切值互为倒数.
随堂练习
4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
3.已知∠A,∠B为锐角,
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
=
=
正切通常也用来描述山坡的坡度.
坡度越大,坡角越大,坡面就越陡.
坡角:坡面与水平面的夹角α称为坡角;
坡度(坡比):坡面的高度h和水平长度l的比称
为坡度i(或坡比),即坡度等于坡角的正切.
i=(坡度通常写成h∶l的形式).
i==tanα
归纳:坡度越大,坡角越大,坡面就越陡.
若某人沿坡度i=3∶4的斜坡前进10米,则他所在的位置比原来的位置升高了_____米.
6
答:i=tanB==,
设AC=3x,BC=4x,
由勾股定理求得x=2,
∴AC=6,即升高6米.
A
B
C
┌
10m
i=3∶4
例3
如图所示,梯形护坡石坝的斜坡AB的坡度i=1∶3,坝高BC=2米,则斜坡AB的长是( )
A.2 B.2 C.4 D.6
解析:∵∠ACB=90°,i=1∶3,
∵BC=2米,
∴i==,
∴AC=3BC=3×2=6(米).
∴AB===2(米).
A
B
C
i=1∶3
2米
【方法总结】理解坡度的概念是解决与坡度有关的计算题的关键.
B
例4
已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离均为h,距形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值为( )
A. B. C. D.
在Rt△BCF中,tanα===,故选C.
解:过A作AE⊥l4于E,过C作CF⊥l4于F,
∵∠ABE+∠α=∠α+∠BCF=90°,
∴∠ABE=∠BCF,
∴Rt△ABE∽Rt△BCF,=,即= ,
∴BF=,
B
D
A
C
l4
l3
l2
l1
F
E
C
例5
随堂练习
1.如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于( )
A. B.
C. D.
C
2.如图②,某水库堤坝横断面迎水坡AB的坡比是1∶,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.100m
C.150m D.50m
随堂练习
3.已知如图③:在Rt△ABC中,∠ACB=90°,CD⊥AB,∠ACD=α,AC=1,BC=3,则tanα=_____.
②
③
A
随堂练习
4. 在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.求锐角三角函数时,勾股定理的运用是很重要的.
┌
D
∵BD=5,AD=12.
解:如图,过点A作AD⊥BC于点D,
∴在Rt△ABD中,
∴tanB==,
A
C
B
13
13
5. 在Rt△ABC中,∠C=90°, AB=15,tanA= ,求AC和BC.
4k
┌
A
C
B
15
3k
随堂练习
解:如图,∵tanA===,
∴(3k)2+(4k)2=152
∴25k2=225.
∴BC=3k=3×3=9.
AC=4k=4×3=12
6. 如图,正方形ABCD的边长为4,点M在BC上,M、N两点关于对角线AC对称, 若DM=1,求tan∠ADN的值.
解:由正方形的性质可知,
∴ DM=1BN=DM=1.
随堂练习
∠ADN=∠DNC,BC=DC=4,
∵ M、N两点关于对角线AC对称,
∴tan∠ADN=tan∠DNC==,
A
D
B
N
M
C
4
1
7. 如图,在平面直角坐标系中,P(x,y)是第一象限内直线y=-x+6上的点, 点A(5,0),O是坐标原点,△PAO的面积为S.
(1)求S与x的函数关系式;
(2)当S=10时,求tan∠PAO 的值.
M
解:(1)过点P作PM⊥OA于点M,
随堂练习
P
O
A
x
y
(x,y)
S=×OA×PM= y
又∵点P在直线y=-x+6上,
∴x=2.
∴AM=OA-OM=5-2=3.
如图,在平面直角坐标系中,P(x,y)是第一象限内直线y=-x+6上的点, 点A(5,0),O是坐标原点,△PAO的面积为S.
(2)当S=10时,求tan∠PAO 的值.
解:∵S= y=10,
∴ y=4,
∴tan∠PAO==,
M
P
O
A
x
y
(x,y)
随堂练习
正切
定义
与梯子倾斜程度的关系
坡度
∠A越大,tanA越大,
梯子越陡
tanA=
∠A的对边
∠A的邻边
i=tanα=
铅直距离
水平距离
第二十三章 解直角三角形
23.1 锐角的三角函数
第1课时 正切
直角三角形中某个锐角的正切值;了解坡度的有关概念.
理解正切、倾斜程度、坡度的数学意义,密切数学与生活的联系.
理解正切的意义,并用它来表示两边的比.
正切
图片欣赏
思考:衡量山“险”与“不险”的标准是什么呢?
陡
陡意味着倾斜程度大
想一想:你能比较两个梯子哪个更陡吗?你有哪些办法?
A
C
B
铅直高度
水平宽度
相关概念
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
梯子与地面的夹角∠ABC称为倾斜角
问题1:你能比较两个梯子哪个更陡吗?你有哪些办法?
A
B
C
D
E
F
倾斜角越大——梯子越陡
4m
2m
A
B
C
4m
3m
F
E
D
问题2:如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度一样,水平宽度越小,梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
4m
2m
E
F
D
3m
2m
A
B
C
问题3:如图,梯子AB和EF哪个更陡?你是怎样判断的?
3m
6m
D
E
F
C
2m
B
4m
A
当铅直高度与水平宽度的比相等时,梯子一样陡
问题4:如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度与水平宽度的比越大,梯子越陡.
倾斜角越大,梯子越陡.
2m
5m
A
B
C
3m
6m
D
E
F
1.探究:(1)Rt△AB1C1和RtAB2C2有什么关系?
2.和有什么关系?
3.如果改变B2C2在梯子上的位置(如B3C3),和有什么关系?
B3
B2
C2
C3
A
C1
B1
Rt△AB1C1∽Rt△AB2C2;
=
=
由此你得出什么结论?
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,
即
A
B
C
∠A的对边
∠A的邻边
┌
斜边∠C
结论:tanA的值越大,梯子越陡.
tanA=
∠A的对边
∠A的邻边
4.tanA不表示“tan”乘以“A ”.
定义中的几点说明:
1.初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2.tanA是一个完整的符号,它表示∠A的正切.但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3.tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序:).
5.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
锐角A的正切值可以等于1吗?为什么?可以大于1吗?
对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.
解:可以等于1,此时为等腰直角三角形;也可以大于1,甚至可逼近于无穷大.
议一议
A
B
C
如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗?
∴CD=1.5,
解:∵△ABC是等腰直角三角形,BD⊥AC,
∴tanC===1.
1.5
A
B
C
D
3
例1
下图表示两个自动扶梯,哪一个自动扶梯比较陡
β
6m
乙
8m
α
5m
甲
13m
解:甲梯中,tanα==
乙梯中,tanβ = =
∵tanβ>tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
例2
tanB= =
( )
BC
( )
BD
tanA= =
( )
AC
( )
AD
随堂练习
1. 在Rt△ABC中,∠C=90°,AC=7,BC=5,则
tan A=_____,tanB =______.
2.下图中∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
BC
CD
AC
CD
互余两锐角的正切值互为倒数.
随堂练习
4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
3.已知∠A,∠B为锐角,
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
=
=
正切通常也用来描述山坡的坡度.
坡度越大,坡角越大,坡面就越陡.
坡角:坡面与水平面的夹角α称为坡角;
坡度(坡比):坡面的高度h和水平长度l的比称
为坡度i(或坡比),即坡度等于坡角的正切.
i=(坡度通常写成h∶l的形式).
i==tanα
归纳:坡度越大,坡角越大,坡面就越陡.
若某人沿坡度i=3∶4的斜坡前进10米,则他所在的位置比原来的位置升高了_____米.
6
答:i=tanB==,
设AC=3x,BC=4x,
由勾股定理求得x=2,
∴AC=6,即升高6米.
A
B
C
┌
10m
i=3∶4
例3
如图所示,梯形护坡石坝的斜坡AB的坡度i=1∶3,坝高BC=2米,则斜坡AB的长是( )
A.2 B.2 C.4 D.6
解析:∵∠ACB=90°,i=1∶3,
∵BC=2米,
∴i==,
∴AC=3BC=3×2=6(米).
∴AB===2(米).
A
B
C
i=1∶3
2米
【方法总结】理解坡度的概念是解决与坡度有关的计算题的关键.
B
例4
已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离均为h,距形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值为( )
A. B. C. D.
在Rt△BCF中,tanα===,故选C.
解:过A作AE⊥l4于E,过C作CF⊥l4于F,
∵∠ABE+∠α=∠α+∠BCF=90°,
∴∠ABE=∠BCF,
∴Rt△ABE∽Rt△BCF,=,即= ,
∴BF=,
B
D
A
C
l4
l3
l2
l1
F
E
C
例5
随堂练习
1.如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于( )
A. B.
C. D.
C
2.如图②,某水库堤坝横断面迎水坡AB的坡比是1∶,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.100m
C.150m D.50m
随堂练习
3.已知如图③:在Rt△ABC中,∠ACB=90°,CD⊥AB,∠ACD=α,AC=1,BC=3,则tanα=_____.
②
③
A
随堂练习
4. 在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.求锐角三角函数时,勾股定理的运用是很重要的.
┌
D
∵BD=5,AD=12.
解:如图,过点A作AD⊥BC于点D,
∴在Rt△ABD中,
∴tanB==,
A
C
B
13
13
5. 在Rt△ABC中,∠C=90°, AB=15,tanA= ,求AC和BC.
4k
┌
A
C
B
15
3k
随堂练习
解:如图,∵tanA===,
∴(3k)2+(4k)2=152
∴25k2=225.
∴BC=3k=3×3=9.
AC=4k=4×3=12
6. 如图,正方形ABCD的边长为4,点M在BC上,M、N两点关于对角线AC对称, 若DM=1,求tan∠ADN的值.
解:由正方形的性质可知,
∴ DM=1BN=DM=1.
随堂练习
∠ADN=∠DNC,BC=DC=4,
∵ M、N两点关于对角线AC对称,
∴tan∠ADN=tan∠DNC==,
A
D
B
N
M
C
4
1
7. 如图,在平面直角坐标系中,P(x,y)是第一象限内直线y=-x+6上的点, 点A(5,0),O是坐标原点,△PAO的面积为S.
(1)求S与x的函数关系式;
(2)当S=10时,求tan∠PAO 的值.
M
解:(1)过点P作PM⊥OA于点M,
随堂练习
P
O
A
x
y
(x,y)
S=×OA×PM= y
又∵点P在直线y=-x+6上,
∴x=2.
∴AM=OA-OM=5-2=3.
如图,在平面直角坐标系中,P(x,y)是第一象限内直线y=-x+6上的点, 点A(5,0),O是坐标原点,△PAO的面积为S.
(2)当S=10时,求tan∠PAO 的值.
解:∵S= y=10,
∴ y=4,
∴tan∠PAO==,
M
P
O
A
x
y
(x,y)
随堂练习
正切
定义
与梯子倾斜程度的关系
坡度
∠A越大,tanA越大,
梯子越陡
tanA=
∠A的对边
∠A的邻边
i=tanα=
铅直距离
水平距离
