沪科版九年级数学上册 23.2.4 坡度与解直角三角形 课件(共30张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 23.2.4 坡度与解直角三角形 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:40:34 | ||
图片预览





文档简介
(共30张PPT)
第二十三章 解直角三角形
23.2 解直角三角形及其应用
第4课时 坡度与解直角三角形
了解测量中坡度、坡角的概念.
能利用解直角三角形的知识,解决与坡度、与弧长有关的实际问题.
能利用解直角三角形的知识,解决与坡度有关的实际问题.
坡度与坡角
掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.
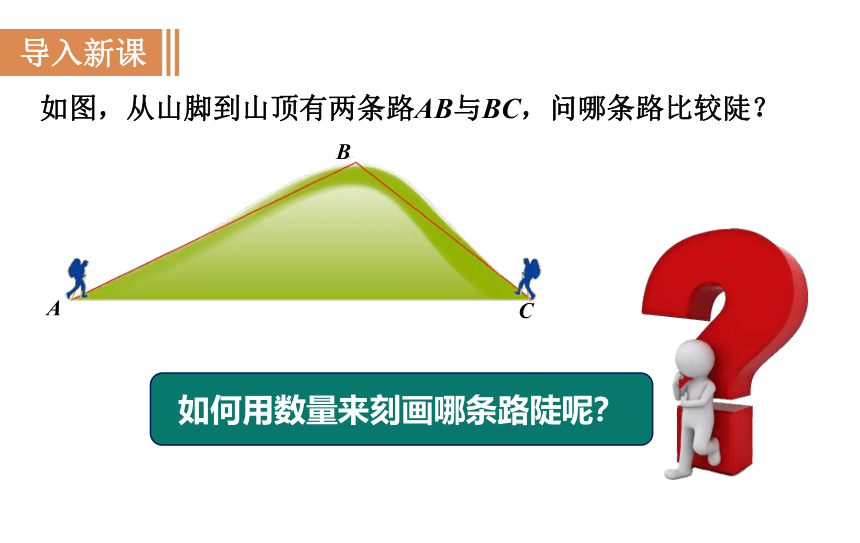
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
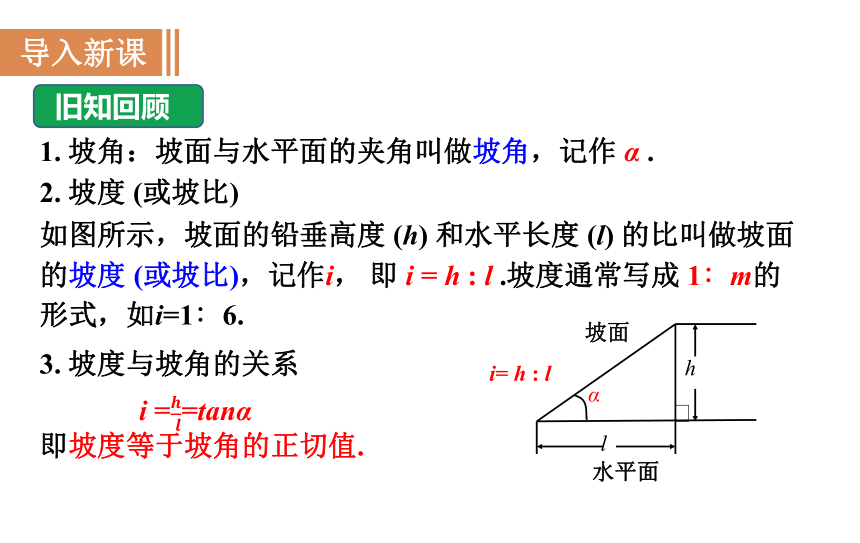
1. 坡角:坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .坡度通常写成 1∶m的形式,如i=1∶6.
旧知回顾
水平面
α
l
h
i= h : l
坡面
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
i ==tanα
30
1 : 1
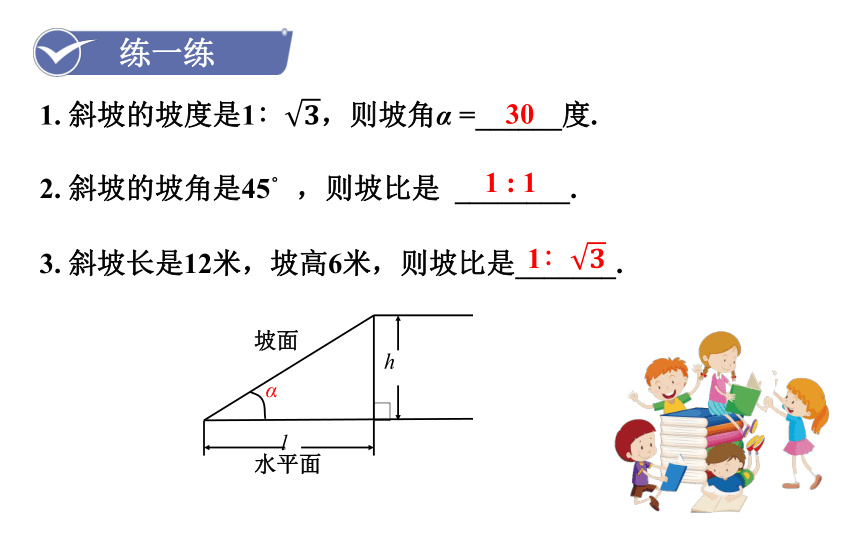
3. 斜坡长是12米,坡高6米,则坡比是_______.
1∶
1. 斜坡的坡度是1∶,则坡角α =______度.
2. 斜坡的坡角是45° ,则坡比是 ________.
练一练
水平面
α
l
h
坡面
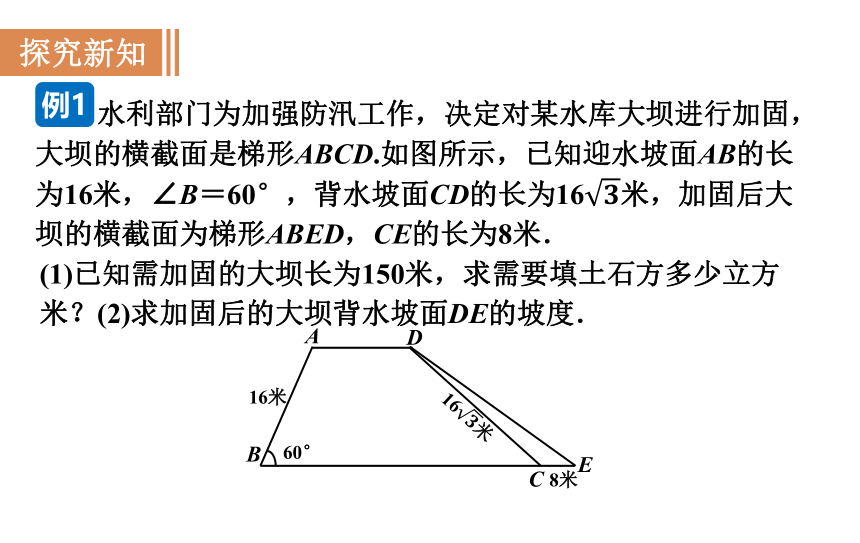
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16米,加固后大坝的横截面为梯形ABED,CE的长为8米.
A
D
B
C
E
60°
16米
16米
8米
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?(2)求加固后的大坝背水坡面DE的坡度.
例1
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
∴需要填土32×150=4800(立方米).
解:如图,分别过A、D作下底的垂线,垂足为F、G,
在Rt△ABF中,AB=16,∠B=60°,
∴AF=16sin60°=8=DG.
又∵CE=8,
∴S△DCE=×8×8=32.
A
D
B
C
E
60°
16米
16米
8米
F
G
(2)求加固后的大坝背水坡面DE的坡度.
tan∠DEG====i.
解:在Rt△DGC中,
CG== =24,
∴GE=24+8=32.
在Rt△DGE中,
A
D
B
C
E
60°
16米
16米
8米
F
G
如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
i=1:2
A
C
B
例2
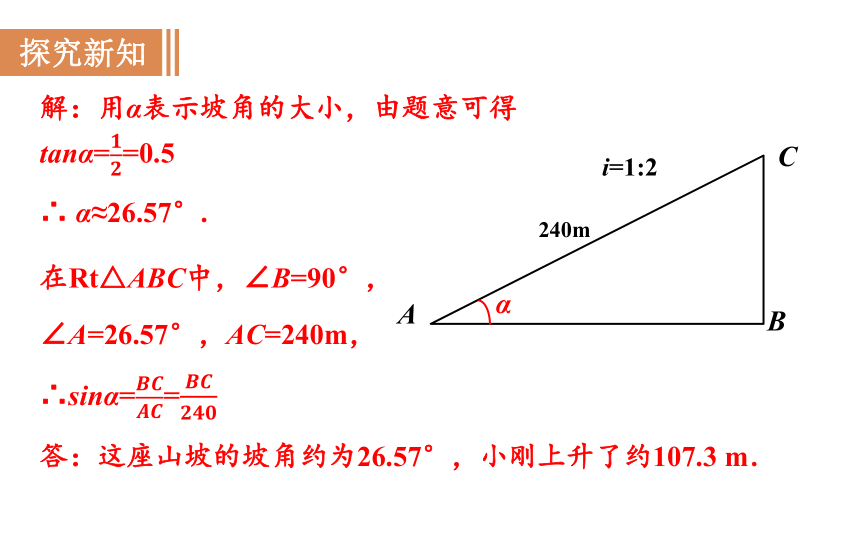
在Rt△ABC中,∠B=90°,
解:用α表示坡角的大小,由题意可得
∴ α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
∴sinα==
tanα==0.5
∠A=26.57°,AC=240m,
i=1:2
A
C
B
240m
α
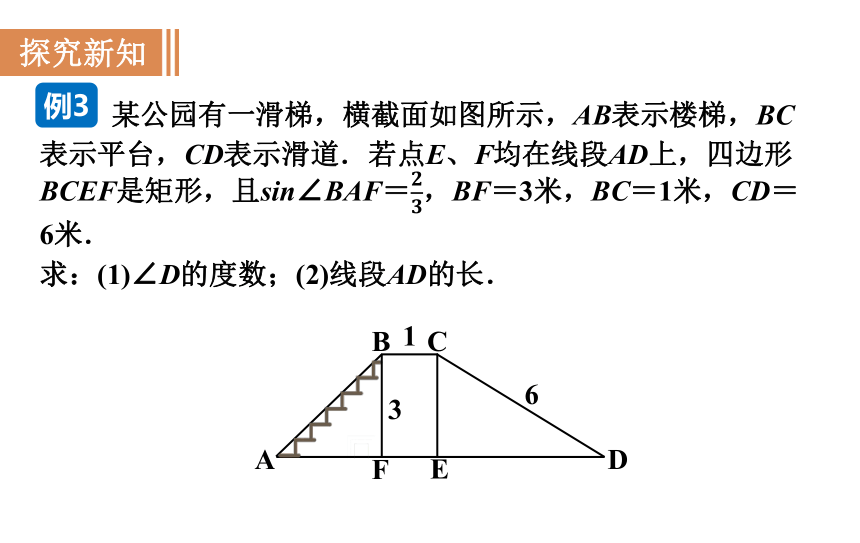
某公园有一滑梯,横截面如图所示,AB表示楼梯,BC表示平台,CD表示滑道.若点E、F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=,BF=3米,BC=1米,CD=6米.
求:(1)∠D的度数;(2)线段AD的长.
A
D
B
C
E
F
3
6
1
例3
∴∠D=30°.
解:∵四边形BCEF是矩形,
∴∠BFE=∠CEF=90°,
∴∠BFA=∠CED=90°,CE=BF=3米,
∵CD=6米
A
D
B
C
E
F
3
6
1
(1)∠D的度数;
∴sin∠CDE=,
∴AD=AF+FE+ED
解:∵sin∠BAF=,
∴= ,
∵BF=3米,
∴AB=m,
∴AF==m,
∵CD=6米,∠CED=90°,
∠D=30°,
∴cos30°=,
∴DE=3m,
(2)线段AD的长.
=(+1+3 )m.
A
D
B
C
E
F
3
6
1
铁路路基的横断面是四边形ABCD,AD∥BC,路基宽BC=9.8m,高BE=5.8m,斜坡AB的坡度i=1∶1.6,斜坡CD的坡度i=1∶2.5,求:底宽AB和斜坡的坡角α和β (精确到 1°);
A
D
B
C
i=1:2.5
5.8
9.8
α
β
i=1:1.6
E
例4
解: 过C作CF⊥AD于点F,
得CF=BE,EF=BC,∠A=α,∠B=β.
BE=5.8m,=,=,
∴AD=AE+EF+DF
=9.28+9.8+14.5≈33.6(m).
∴AE=1.6×5.8=9.28(m),
DF=2.5×5.8=14.5(m).
∵tanα=i=tanβ=i′=,
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和21°
α≈32°,β≈21°.
A
D
B
C
i=1:2.5
5.8
9.8
α
β
i=1:1.6
E
F
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
思考
h
l
α
h
α
l
我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角α1,这样就可以算出这段山坡的高度h1=l1sinα1.
h1
l1
α1
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l.
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
随堂练习
1.(德州中考)如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1∶2,则斜坡AB的长为( )
A.4m B.6m
C.12m D.24 m
h
i=1∶2
α
A
B
C
E
D
B
随堂练习
2.如图,某铁路路基的横断面是四边形ABCD,AD∥BC,已知路基高AE为5米,左侧坡面AB长10米,则左侧坡面AB的坡度为( )
A.1∶2 B.1∶
C.1∶ D.1∶
A
C
B
D
E
5m
10m
C
随堂练习
3.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为
( )
A.5cosα米 B. 米 C.5sinα米 D. 米
5米
α
B
A
B
随堂练习
4.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上.如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
30°
A.(6+ )米 B.12米
C.(4+2)米 D.10米
A
5.水库拦水坝的横断面是四边形ABCD,AD∥BC,背水坡CD的坡比i=1∶1,已知背水坡的坡长CD=24m,则背水坡的坡角α为____,拦水坝的高度为_______m.
6.如图,在坡比为i=1∶2的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是______米.
随堂练习
45°
12
3
(第5题图)
24m
(第6题图)
6
7.某人在D处测得山顶C的仰角为30°,向前走200米到山脚A处,测得山坡AC的坡度为i≈1∶0.5,求山的高度(不计测角仪的高度,≈1.73,结果保留整数).
随堂练习
∴x==162.
解:i==,
设BC=x,
则AB=x.
∵∠D=30°,
∴DB=x,
∴x-x=200,
∴山的高度约为162米.
200米
i≈1∶0.5
8.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6 m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1 m).
随堂练习
55°
A
D
B
C
H
6 m
74°
解:如图,过点A作AE⊥BC于点E,
在Rt△ABE中,sin∠ABE=,
∴AE=ABsin∠ABE=6sin74°≈5.77.
cos∠ABE=,
∴BE=ABcos∠ABE=6cos74°≈1.65.
∵AH∥BC,∴DF=AE≈5.77.
在Rt△BDF中,tan∠DBF=,
∴BF=≈≈4.04
∴AD=EF=BF-BE
过点D作DF⊥BC于点F
≈4.04-1.65≈2.4(m).
55°
A
D
B
C
H
6 m
74°
E
F
随堂练习
9. 一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽 (精确到0.1米,=1.732,=1.414).
45°
30°
4米
12米
A
B
C
D
由题意可知
解:作DE⊥AB, CF⊥AB,
DE=CF=4 (米),
在Rt△ADE中,
∵i===tan45°
答: 路基下底的宽约为22.93米.
AE==4(米)
在Rt△BCF中,同理可得
∴ AB=AE+EF+BF
BF=≈6.93(米)
垂足分别为E、F.
≈4+12+6.93≈22.93 (米).
CD=EF=12 (米).
45°
30°
4米
12米
A
B
C
D
E
F
随堂练习
坡度与解直角三角形
依据
解法:化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
勾股定理
两锐角互余
锐角的三角函数
第二十三章 解直角三角形
23.2 解直角三角形及其应用
第4课时 坡度与解直角三角形
了解测量中坡度、坡角的概念.
能利用解直角三角形的知识,解决与坡度、与弧长有关的实际问题.
能利用解直角三角形的知识,解决与坡度有关的实际问题.
坡度与坡角
掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
1. 坡角:坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .坡度通常写成 1∶m的形式,如i=1∶6.
旧知回顾
水平面
α
l
h
i= h : l
坡面
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
i ==tanα
30
1 : 1
3. 斜坡长是12米,坡高6米,则坡比是_______.
1∶
1. 斜坡的坡度是1∶,则坡角α =______度.
2. 斜坡的坡角是45° ,则坡比是 ________.
练一练
水平面
α
l
h
坡面
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16米,加固后大坝的横截面为梯形ABED,CE的长为8米.
A
D
B
C
E
60°
16米
16米
8米
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?(2)求加固后的大坝背水坡面DE的坡度.
例1
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
∴需要填土32×150=4800(立方米).
解:如图,分别过A、D作下底的垂线,垂足为F、G,
在Rt△ABF中,AB=16,∠B=60°,
∴AF=16sin60°=8=DG.
又∵CE=8,
∴S△DCE=×8×8=32.
A
D
B
C
E
60°
16米
16米
8米
F
G
(2)求加固后的大坝背水坡面DE的坡度.
tan∠DEG====i.
解:在Rt△DGC中,
CG== =24,
∴GE=24+8=32.
在Rt△DGE中,
A
D
B
C
E
60°
16米
16米
8米
F
G
如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
i=1:2
A
C
B
例2
在Rt△ABC中,∠B=90°,
解:用α表示坡角的大小,由题意可得
∴ α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
∴sinα==
tanα==0.5
∠A=26.57°,AC=240m,
i=1:2
A
C
B
240m
α
某公园有一滑梯,横截面如图所示,AB表示楼梯,BC表示平台,CD表示滑道.若点E、F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=,BF=3米,BC=1米,CD=6米.
求:(1)∠D的度数;(2)线段AD的长.
A
D
B
C
E
F
3
6
1
例3
∴∠D=30°.
解:∵四边形BCEF是矩形,
∴∠BFE=∠CEF=90°,
∴∠BFA=∠CED=90°,CE=BF=3米,
∵CD=6米
A
D
B
C
E
F
3
6
1
(1)∠D的度数;
∴sin∠CDE=,
∴AD=AF+FE+ED
解:∵sin∠BAF=,
∴= ,
∵BF=3米,
∴AB=m,
∴AF==m,
∵CD=6米,∠CED=90°,
∠D=30°,
∴cos30°=,
∴DE=3m,
(2)线段AD的长.
=(+1+3 )m.
A
D
B
C
E
F
3
6
1
铁路路基的横断面是四边形ABCD,AD∥BC,路基宽BC=9.8m,高BE=5.8m,斜坡AB的坡度i=1∶1.6,斜坡CD的坡度i=1∶2.5,求:底宽AB和斜坡的坡角α和β (精确到 1°);
A
D
B
C
i=1:2.5
5.8
9.8
α
β
i=1:1.6
E
例4
解: 过C作CF⊥AD于点F,
得CF=BE,EF=BC,∠A=α,∠B=β.
BE=5.8m,=,=,
∴AD=AE+EF+DF
=9.28+9.8+14.5≈33.6(m).
∴AE=1.6×5.8=9.28(m),
DF=2.5×5.8=14.5(m).
∵tanα=i=tanβ=i′=,
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和21°
α≈32°,β≈21°.
A
D
B
C
i=1:2.5
5.8
9.8
α
β
i=1:1.6
E
F
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
思考
h
l
α
h
α
l
我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角α1,这样就可以算出这段山坡的高度h1=l1sinα1.
h1
l1
α1
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l.
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
随堂练习
1.(德州中考)如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1∶2,则斜坡AB的长为( )
A.4m B.6m
C.12m D.24 m
h
i=1∶2
α
A
B
C
E
D
B
随堂练习
2.如图,某铁路路基的横断面是四边形ABCD,AD∥BC,已知路基高AE为5米,左侧坡面AB长10米,则左侧坡面AB的坡度为( )
A.1∶2 B.1∶
C.1∶ D.1∶
A
C
B
D
E
5m
10m
C
随堂练习
3.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为
( )
A.5cosα米 B. 米 C.5sinα米 D. 米
5米
α
B
A
B
随堂练习
4.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上.如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
30°
A.(6+ )米 B.12米
C.(4+2)米 D.10米
A
5.水库拦水坝的横断面是四边形ABCD,AD∥BC,背水坡CD的坡比i=1∶1,已知背水坡的坡长CD=24m,则背水坡的坡角α为____,拦水坝的高度为_______m.
6.如图,在坡比为i=1∶2的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是______米.
随堂练习
45°
12
3
(第5题图)
24m
(第6题图)
6
7.某人在D处测得山顶C的仰角为30°,向前走200米到山脚A处,测得山坡AC的坡度为i≈1∶0.5,求山的高度(不计测角仪的高度,≈1.73,结果保留整数).
随堂练习
∴x==162.
解:i==,
设BC=x,
则AB=x.
∵∠D=30°,
∴DB=x,
∴x-x=200,
∴山的高度约为162米.
200米
i≈1∶0.5
8.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6 m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1 m).
随堂练习
55°
A
D
B
C
H
6 m
74°
解:如图,过点A作AE⊥BC于点E,
在Rt△ABE中,sin∠ABE=,
∴AE=ABsin∠ABE=6sin74°≈5.77.
cos∠ABE=,
∴BE=ABcos∠ABE=6cos74°≈1.65.
∵AH∥BC,∴DF=AE≈5.77.
在Rt△BDF中,tan∠DBF=,
∴BF=≈≈4.04
∴AD=EF=BF-BE
过点D作DF⊥BC于点F
≈4.04-1.65≈2.4(m).
55°
A
D
B
C
H
6 m
74°
E
F
随堂练习
9. 一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽 (精确到0.1米,=1.732,=1.414).
45°
30°
4米
12米
A
B
C
D
由题意可知
解:作DE⊥AB, CF⊥AB,
DE=CF=4 (米),
在Rt△ADE中,
∵i===tan45°
答: 路基下底的宽约为22.93米.
AE==4(米)
在Rt△BCF中,同理可得
∴ AB=AE+EF+BF
BF=≈6.93(米)
垂足分别为E、F.
≈4+12+6.93≈22.93 (米).
CD=EF=12 (米).
45°
30°
4米
12米
A
B
C
D
E
F
随堂练习
坡度与解直角三角形
依据
解法:化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
勾股定理
两锐角互余
锐角的三角函数
