沪科版九年级数学上册 23.1.4 一般锐角的三角函数值 课件(共23张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 23.1.4 一般锐角的三角函数值 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 16:41:02 | ||
图片预览







文档简介
(共23张PPT)
第二十三章 解直角三角形
23.1 锐角的三角函数
第4课时 一般锐角的三角函数值
学会利用计算器求三角函数值并进行相关计算. (重点)
学会利用计算器根据三角函数值求锐角度数并计算.(难点).
一般锐角的三角函数值
复习并巩固锐角三角函数的相关知识.
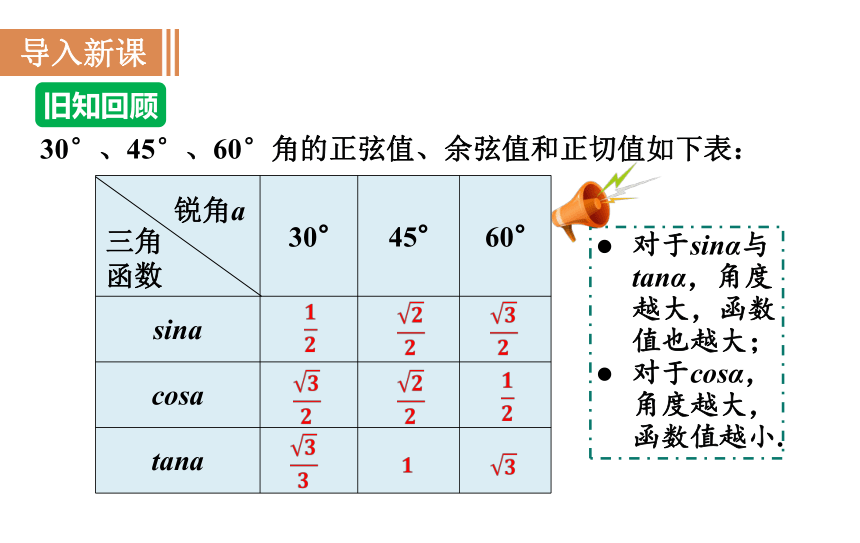
30°、45°、60°角的正弦值、余弦值和正切值如下表:
30° 45° 60°
sina
cosa
tana
三角函数
锐角a
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小.
旧知回顾
D
A
B
E
1.6m
20m
45°
C
问题:升国旗时,小明站在操场上离国旗20m处行注目礼.当国旗升至顶端时,小明看国旗视线的仰角为42°(如图所示),若小明双眼离地面1.60m,你能帮助小明求出旗杆AB的高度吗?
解:由已知得DC=EB=20cm
∵tan∠ADC=tan42°= ,
∴AC=DC·tan42°,
∴AB=AC+CB=20·tan42°+1.6,
这里的tan42°是多少呢?
第一步:按计算器 键,
sin
求sin18°
屏幕显示答案:sin18°=0.309 016 994;
第一种方法:
第二步:输入角度值18,
(也有的计算器是先输入角度再按函数名称键).
用计算器求三角函数值
例1
第一步:按计算器 键,
tan
求tan30°36'.
屏幕显示答案:0.591 398 351;
第一种方法:
第二种方法:
第一步:按计算器 键,
tan
第二步:输入角度值30.6 (因为30°36'=30.6°)
屏幕显示答案:0.591 398 351.
第二步:输入角度值30,分值36 (可以使用 键),
°'″
例2
1.求sin63°52′41″的值.(精确到0.0001)
先用如下方法将角度单位状态设定为“度”:MODE MODE 1
显示结果为0.897 859 012.所以sin63°52′41″≈0.8979
显示D再按下列顺序依次按键:sin 63 ′″ 52 ′″ 41 ′″ =
解:
练一练
2.用计算器求下列各式的值(精确到0.0001):
(1)cos34°35′; (2)tan66°15′17'';
(3)sin47°; (4)sin18°+cos55°-tan59°.
(3)sin47°≈0.7314;
练一练
解:根据题意用计算器求出:
(1)cos34°35′≈0.8233;
(4)sin18°+cos55°-tan59°≈-0.7817.
(2)tan66°15′17''≈2.2732;
利用计算器求锐角的度数
如果已知锐角三角函数值,可以使用计算器求出相应的锐角.
已知sinA=0.5086,用计算器求锐角A可以按照下面方法操作:
第一步:按计算器 键,
2nd F
sin
第二步:然后输入函数值0. 5086
屏幕显示答案: 30.57062136°
还以以利用 键,进一步得到∠A=30°34'14 ".
°'″
2nd F
已知锐角α的三角函数值,求锐角α的值:
(1)sinα=0.6325;(2)cosα=0.3894;(3)tanα=3.5492
例3
解:(1)依次按键 ,然后输入函数值0.6325,得到结果α=39.23480979°;
2nd F
sin
(2)依次按键 ,然后输入函数值0.3894,得到结果α=67.0828292°;
2nd F
cos
(3)依次按键 ,然后输入函数值3.5492,得到结果α=74.26462479°.
2nd F
tan
练一练
已知下列锐角三角函数值,用计算器求锐角∠A,∠B的度数(结果精确到0.1°):
(1)sinA=0.7,sinB=0.01;
(2)cosA=0.15,cosB=0.8;
(3)tanA=2.4,tanB=0.5.
(3)由tanA=2.4,得∠A≈67.4°;由tanB=0.5,得∠B≈26.6°.
(1)由sinA=0.7,得∠A≈44.4°;由sinB=0.01,得∠B≈0.6°;
(2)由cosA=0.15,得∠A≈81.4°;由cosB=0.8,得∠B≈36.9°;
解:
cos55°=
cos70°=
cos74°28 '=
tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
0.3420
0.3420
0.5735
0.5735
0.2678
0.2678
5.930
0.0547
角度增大
正弦值增大
余弦值减小
正切值增大
比一比,你能得出什么结论?
tan3°8 ' =
正切值随着角度的增大(或减小)而增大(或减小).
正弦值随着角度的增大(或减小)而增大(或减小);
余弦值随着角度的增大(或减小)而减小(或增大);
利用三角函数解决实际问题
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)
例4
C
A
B
45°
25°
10
(1)求改直后的公路AB的长;
∵∠CBA=45°,∴BD=CD=4.2(千米),
所以,改直后的公路AB的长约为13.3千米;
解:(1)过点C作CD⊥AB于点D,
∵AC=10千米,∠CAB=25°,
∴CD=sin∠CAB·AC=sin25°×10≈0.42×10=4.2(千米),
AD=cos∠CAB·AC=cos25°×10≈0.91×10=9.1(千米).
∴AB=AD+BD=9.1+4.2=13.3(千米).
BC= = ≈5.9(千米).
∵∠CBA=45°,∴BD=CD=4.2(千米),
D
C
A
B
45°
25°
10
(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)
所以,公路改直后该段路程比原来缩短了约2.6千米.
【方法总结】解决问题的关键是作出辅助线,构造直角三角形,利用三角函数关系求出有关线段的长.
D
C
A
B
45°
25°
10
解:∵AC=10千米,BC=5.9千米,
∴AC+BC-AB=10+5.9-13.3=2.6(千米).
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米
(结果精确到个位).
例5
B
E
N
D
A
45°
61.4°
25.6°
所以,塔高DE大约是81米.
解:延长DE交AB延长线于点F,则∠DFA=90°.
∵∠A=45°,
∴AF=DF.
设EF=x,
∴BF=2x,则DF=AF=50+2x,
解得x≈31.
故DE=DF-EF=50+31×2-31=81(米).
∵tan25.6°= ≈0.5,
故tan61.4°= = =1.8,
B
E
N
D
A
45°
61.4°
25.6°
F
随堂练习
1. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627 5,sinB=0.054 7;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 5,tanB=0.881 6.
∠B=38°8″
∠A=38°51′57″
∠A=51°18′11″
∠B=80°27′2″
∠A=78°19′58″
∠B=41°23′58″
随堂练习
2.在Rt△ABC中,∠C=90°,则下列式子定成立的是( )
A.sinA=sinB B.cosA=cosB
C.tanA=tanB D.sinA=cosB
3.已知:sin232°+cos2α=1,则锐角α等于( )
A.32° B.58°
C.68° D.以上结论都不对
D
B
4.如图,在Rt△ABC中,∠C=90°,∠A=35°,AC=6,求BC,AB的长(精确到0.001).
解:因为 =tanA=tan35°,
由计算器求得tan35°≈0.7002,
所以BC=AC·tanA≈6×0.7002≈4.201,
又 =cosA≈cos35°,
由计算器求得cos35°=0.8192,
所以AB= ≈7.324.
35°
6
随堂练习
5.如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到度).
∴V型角的大小约为55°.
由计算器求得∠ACD≈27.51°,
∴∠ACB=2∠ACD≈2×27.51°≈55°.
解:∵tan∠ACD= = ≈0.5208,
20mm
19.2mm
随堂练习
三角函数的计算
用计算器求锐角的三角函数值或角的度数
不同的计算器操作步骤可能有所不同
利用计算器探索锐三角函数的新知
第二十三章 解直角三角形
23.1 锐角的三角函数
第4课时 一般锐角的三角函数值
学会利用计算器求三角函数值并进行相关计算. (重点)
学会利用计算器根据三角函数值求锐角度数并计算.(难点).
一般锐角的三角函数值
复习并巩固锐角三角函数的相关知识.
30°、45°、60°角的正弦值、余弦值和正切值如下表:
30° 45° 60°
sina
cosa
tana
三角函数
锐角a
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小.
旧知回顾
D
A
B
E
1.6m
20m
45°
C
问题:升国旗时,小明站在操场上离国旗20m处行注目礼.当国旗升至顶端时,小明看国旗视线的仰角为42°(如图所示),若小明双眼离地面1.60m,你能帮助小明求出旗杆AB的高度吗?
解:由已知得DC=EB=20cm
∵tan∠ADC=tan42°= ,
∴AC=DC·tan42°,
∴AB=AC+CB=20·tan42°+1.6,
这里的tan42°是多少呢?
第一步:按计算器 键,
sin
求sin18°
屏幕显示答案:sin18°=0.309 016 994;
第一种方法:
第二步:输入角度值18,
(也有的计算器是先输入角度再按函数名称键).
用计算器求三角函数值
例1
第一步:按计算器 键,
tan
求tan30°36'.
屏幕显示答案:0.591 398 351;
第一种方法:
第二种方法:
第一步:按计算器 键,
tan
第二步:输入角度值30.6 (因为30°36'=30.6°)
屏幕显示答案:0.591 398 351.
第二步:输入角度值30,分值36 (可以使用 键),
°'″
例2
1.求sin63°52′41″的值.(精确到0.0001)
先用如下方法将角度单位状态设定为“度”:MODE MODE 1
显示结果为0.897 859 012.所以sin63°52′41″≈0.8979
显示D再按下列顺序依次按键:sin 63 ′″ 52 ′″ 41 ′″ =
解:
练一练
2.用计算器求下列各式的值(精确到0.0001):
(1)cos34°35′; (2)tan66°15′17'';
(3)sin47°; (4)sin18°+cos55°-tan59°.
(3)sin47°≈0.7314;
练一练
解:根据题意用计算器求出:
(1)cos34°35′≈0.8233;
(4)sin18°+cos55°-tan59°≈-0.7817.
(2)tan66°15′17''≈2.2732;
利用计算器求锐角的度数
如果已知锐角三角函数值,可以使用计算器求出相应的锐角.
已知sinA=0.5086,用计算器求锐角A可以按照下面方法操作:
第一步:按计算器 键,
2nd F
sin
第二步:然后输入函数值0. 5086
屏幕显示答案: 30.57062136°
还以以利用 键,进一步得到∠A=30°34'14 ".
°'″
2nd F
已知锐角α的三角函数值,求锐角α的值:
(1)sinα=0.6325;(2)cosα=0.3894;(3)tanα=3.5492
例3
解:(1)依次按键 ,然后输入函数值0.6325,得到结果α=39.23480979°;
2nd F
sin
(2)依次按键 ,然后输入函数值0.3894,得到结果α=67.0828292°;
2nd F
cos
(3)依次按键 ,然后输入函数值3.5492,得到结果α=74.26462479°.
2nd F
tan
练一练
已知下列锐角三角函数值,用计算器求锐角∠A,∠B的度数(结果精确到0.1°):
(1)sinA=0.7,sinB=0.01;
(2)cosA=0.15,cosB=0.8;
(3)tanA=2.4,tanB=0.5.
(3)由tanA=2.4,得∠A≈67.4°;由tanB=0.5,得∠B≈26.6°.
(1)由sinA=0.7,得∠A≈44.4°;由sinB=0.01,得∠B≈0.6°;
(2)由cosA=0.15,得∠A≈81.4°;由cosB=0.8,得∠B≈36.9°;
解:
cos55°=
cos70°=
cos74°28 '=
tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
0.3420
0.3420
0.5735
0.5735
0.2678
0.2678
5.930
0.0547
角度增大
正弦值增大
余弦值减小
正切值增大
比一比,你能得出什么结论?
tan3°8 ' =
正切值随着角度的增大(或减小)而增大(或减小).
正弦值随着角度的增大(或减小)而增大(或减小);
余弦值随着角度的增大(或减小)而减小(或增大);
利用三角函数解决实际问题
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)
例4
C
A
B
45°
25°
10
(1)求改直后的公路AB的长;
∵∠CBA=45°,∴BD=CD=4.2(千米),
所以,改直后的公路AB的长约为13.3千米;
解:(1)过点C作CD⊥AB于点D,
∵AC=10千米,∠CAB=25°,
∴CD=sin∠CAB·AC=sin25°×10≈0.42×10=4.2(千米),
AD=cos∠CAB·AC=cos25°×10≈0.91×10=9.1(千米).
∴AB=AD+BD=9.1+4.2=13.3(千米).
BC= = ≈5.9(千米).
∵∠CBA=45°,∴BD=CD=4.2(千米),
D
C
A
B
45°
25°
10
(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)
所以,公路改直后该段路程比原来缩短了约2.6千米.
【方法总结】解决问题的关键是作出辅助线,构造直角三角形,利用三角函数关系求出有关线段的长.
D
C
A
B
45°
25°
10
解:∵AC=10千米,BC=5.9千米,
∴AC+BC-AB=10+5.9-13.3=2.6(千米).
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米
(结果精确到个位).
例5
B
E
N
D
A
45°
61.4°
25.6°
所以,塔高DE大约是81米.
解:延长DE交AB延长线于点F,则∠DFA=90°.
∵∠A=45°,
∴AF=DF.
设EF=x,
∴BF=2x,则DF=AF=50+2x,
解得x≈31.
故DE=DF-EF=50+31×2-31=81(米).
∵tan25.6°= ≈0.5,
故tan61.4°= = =1.8,
B
E
N
D
A
45°
61.4°
25.6°
F
随堂练习
1. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627 5,sinB=0.054 7;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 5,tanB=0.881 6.
∠B=38°8″
∠A=38°51′57″
∠A=51°18′11″
∠B=80°27′2″
∠A=78°19′58″
∠B=41°23′58″
随堂练习
2.在Rt△ABC中,∠C=90°,则下列式子定成立的是( )
A.sinA=sinB B.cosA=cosB
C.tanA=tanB D.sinA=cosB
3.已知:sin232°+cos2α=1,则锐角α等于( )
A.32° B.58°
C.68° D.以上结论都不对
D
B
4.如图,在Rt△ABC中,∠C=90°,∠A=35°,AC=6,求BC,AB的长(精确到0.001).
解:因为 =tanA=tan35°,
由计算器求得tan35°≈0.7002,
所以BC=AC·tanA≈6×0.7002≈4.201,
又 =cosA≈cos35°,
由计算器求得cos35°=0.8192,
所以AB= ≈7.324.
35°
6
随堂练习
5.如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到度).
∴V型角的大小约为55°.
由计算器求得∠ACD≈27.51°,
∴∠ACB=2∠ACD≈2×27.51°≈55°.
解:∵tan∠ACD= = ≈0.5208,
20mm
19.2mm
随堂练习
三角函数的计算
用计算器求锐角的三角函数值或角的度数
不同的计算器操作步骤可能有所不同
利用计算器探索锐三角函数的新知
