10.1平方根(3)[下学期]
文档属性
| 名称 | 10.1平方根(3)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-12 00:00:00 | ||
图片预览








文档简介
课件28张PPT。
10.1 平方根(3) 小丽想用一块面积为 400cm2
正方形纸片,沿着边的方向裁出一块
面积为300cm2的长方形纸片用来绘
画,使它的长宽之比为3:2, 不知能否裁出来,正在发愁。小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗? 小丽能用这块纸片裁出符合要求的纸片吗?例3:小丽想用一块面积为400cm2的正方形纸片沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,不知能否裁出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?解:设长方形纸片的长为3x cm,宽为2x cm. 根据边长与面积的关系得已知正方形纸片的边长只有20cm,这样,长方形纸片的长将大于正方形纸片的边长.答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.若x2=a(x≥0),那么x叫做a的算术平方根。
记作:x=一般地,如果一个数的平方等于a,
那么这个数叫做a的平方根或二次方根。即:若x2=a,那么x叫做a的平方根。
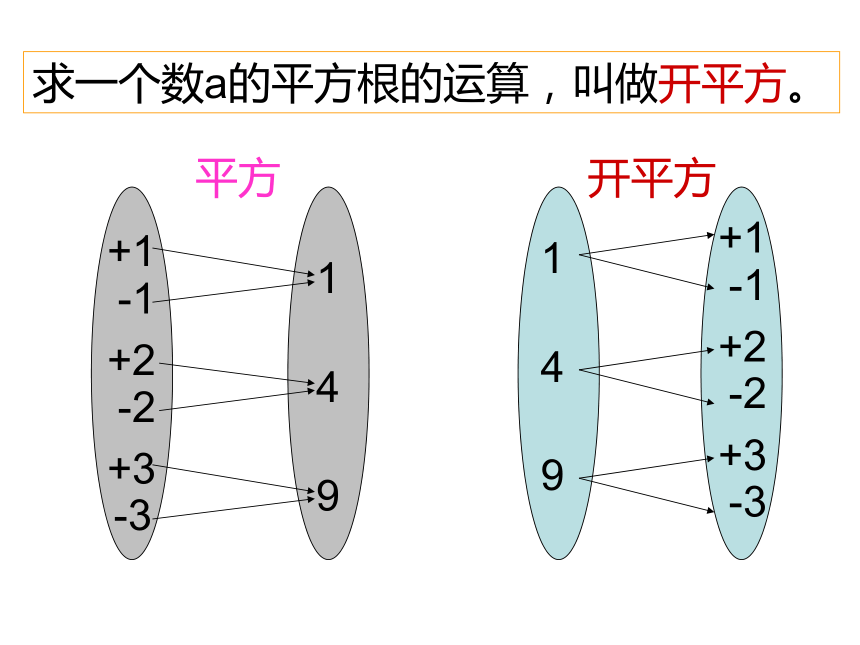
记作:x=求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方例如:∵∴5 和 -5 都是25的平方根。∵∴ 和 - 都是 的平方根。25的平方根是±5±63±2试一试:(1)144的平方根是什么? (2)0的平方根是什么? (3) 的平方根是什么?
(4)-4的平方根是什么?为什么?从上面的回答中,你发现了什么?练习:下列说法中不正确的个数有 ( )
①0.25的平方根是0.5
②-0.5的平方 根是-0.25
③只有正数才有平方根
④0的平方根是0CA. 1个 B. 2个. C. 3个 D. 4个正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。正数a的正的平方根叫做a的算术平方根。正数a的算术平方根记作:它的另一个平方根记作:一个正数a的平方根表示为:0的算术平方根还是0说明:这样求一个正数的平方根,只要求出它的算术平方根后,就可以写出它的平方根了。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。平方与开平方是互为逆运算.举一个实际例子吧!5 的平方根,可以记作 和- ,或± 注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。即式子 中的 a 是一个非负数。 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。(1)81
(2)-81
(3)0
(4)
(5) 例2:求下列各数的平方根。(1)100;(2)1.44;(3) ;(4)解: (1)∴100的平方根是±10即注意:不能写成请你妨照上面的例子完成其余三个小题。学习小结:本节课我们学习了哪些内容,你能回答吗?1.平方根的概念:一个数的平方等于a,这个数叫做a的平方根.2.平方根的性质:一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.3.平方根的表示法:4.算术平方根的概念:正数a的正的平方根叫做a的算术平方根比一比看谁最聪明?如图,求左圈和右圈中的表示的数:?练一练:
求出下列各数的平方根(1)225(2)(3)6.25(4)用计算器求下列各数的算术平方根(1) 529; (2)1225; (3)44.81思考: 你能求出下列各式中的未知数x吗?
(1) x2=49
(2)(x-1)2=25想一想判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( )3.a2的算术平方根是a. ( )4.若 ,则a=-5. ( )5. . ( )6.-6是(-6)2的平方根. ( )7.若x2=36,则x= ( ) 8.如果两个数平方后相等,那么它们的也相等×××××√√例2. 已知 有意义,则x一定是 ( )
A.正数 B. 负数 C. 非负数 D. 非正数例3.求下列各式的值例3. 求使 有意义x的取值范围.例4.已知a、b满足等式 +︱b+5︱=0, 求a2-12b的算术平方根.X≤0补充练习;213256≥0-5互为相反数我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。补充练习:练习:国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间,现有一个长方形的足球场其长是宽的1.5倍,面积为7560m2,问:这个足球场能用作国际比赛吗?作业: 书本p167 3,4,8,10课后思考题:
正方形纸片,沿着边的方向裁出一块
面积为300cm2的长方形纸片用来绘
画,使它的长宽之比为3:2, 不知能否裁出来,正在发愁。小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗? 小丽能用这块纸片裁出符合要求的纸片吗?例3:小丽想用一块面积为400cm2的正方形纸片沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,不知能否裁出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?解:设长方形纸片的长为3x cm,宽为2x cm. 根据边长与面积的关系得已知正方形纸片的边长只有20cm,这样,长方形纸片的长将大于正方形纸片的边长.答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.若x2=a(x≥0),那么x叫做a的算术平方根。
记作:x=一般地,如果一个数的平方等于a,
那么这个数叫做a的平方根或二次方根。即:若x2=a,那么x叫做a的平方根。
记作:x=求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方例如:∵∴5 和 -5 都是25的平方根。∵∴ 和 - 都是 的平方根。25的平方根是±5±63±2试一试:(1)144的平方根是什么? (2)0的平方根是什么? (3) 的平方根是什么?
(4)-4的平方根是什么?为什么?从上面的回答中,你发现了什么?练习:下列说法中不正确的个数有 ( )
①0.25的平方根是0.5
②-0.5的平方 根是-0.25
③只有正数才有平方根
④0的平方根是0CA. 1个 B. 2个. C. 3个 D. 4个正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。正数a的正的平方根叫做a的算术平方根。正数a的算术平方根记作:它的另一个平方根记作:一个正数a的平方根表示为:0的算术平方根还是0说明:这样求一个正数的平方根,只要求出它的算术平方根后,就可以写出它的平方根了。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。平方与开平方是互为逆运算.举一个实际例子吧!5 的平方根,可以记作 和- ,或± 注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。即式子 中的 a 是一个非负数。 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。(1)81
(2)-81
(3)0
(4)
(5) 例2:求下列各数的平方根。(1)100;(2)1.44;(3) ;(4)解: (1)∴100的平方根是±10即注意:不能写成请你妨照上面的例子完成其余三个小题。学习小结:本节课我们学习了哪些内容,你能回答吗?1.平方根的概念:一个数的平方等于a,这个数叫做a的平方根.2.平方根的性质:一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.3.平方根的表示法:4.算术平方根的概念:正数a的正的平方根叫做a的算术平方根比一比看谁最聪明?如图,求左圈和右圈中的表示的数:?练一练:
求出下列各数的平方根(1)225(2)(3)6.25(4)用计算器求下列各数的算术平方根(1) 529; (2)1225; (3)44.81思考: 你能求出下列各式中的未知数x吗?
(1) x2=49
(2)(x-1)2=25想一想判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( )3.a2的算术平方根是a. ( )4.若 ,则a=-5. ( )5. . ( )6.-6是(-6)2的平方根. ( )7.若x2=36,则x= ( ) 8.如果两个数平方后相等,那么它们的也相等×××××√√例2. 已知 有意义,则x一定是 ( )
A.正数 B. 负数 C. 非负数 D. 非正数例3.求下列各式的值例3. 求使 有意义x的取值范围.例4.已知a、b满足等式 +︱b+5︱=0, 求a2-12b的算术平方根.X≤0补充练习;213256≥0-5互为相反数我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。补充练习:练习:国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间,现有一个长方形的足球场其长是宽的1.5倍,面积为7560m2,问:这个足球场能用作国际比赛吗?作业: 书本p167 3,4,8,10课后思考题:
