14.1.1同底数幂的乘法 课件(21张PPT)
文档属性
| 名称 | 14.1.1同底数幂的乘法 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 17:45:30 | ||
图片预览








文档简介
(共21张PPT)
14.1.1 同底数幂的乘法
人教版八年级上册
教学目标
1、理解同底数幂乘法的性质,并能进行简单的运算
2、在探索性质的过程中让学生经历观察、猜想、交流、验证、归纳总结的思维过程,让学生体会由特殊到一般再到特殊的思维方法和辩证的数学思想。
3、引导学生自主探索,体验成功的快乐,增强对数学学习的兴趣,在轻松、和谐有序的教学氛围中,培养学生的个性。
新知导入
一种电子计算机每秒可进行1千万亿(1015 ) 次运算,它工作103 s 可进行多少次运算?
列式:1015×103
怎样计算1015×103呢?
归纳:
底数相同的幂叫做同底数幂。
复习回顾
1、an 表示的意义是什么?其中a、n、an分别叫做什么
2、(-a)n 表示的意义是什么?底数、指数分别是什么?
3、10×10×10×10×10 可以写成________
意义:表示n个a相乘
a叫底数,n叫指数,an叫幂.
意义:表示n个-a相乘
-a叫底数,n叫指数,(-a)n叫幂.
105
新知讲解
根据乘方的意义可知
新知讲解
根据乘方的意义填空,观察计算结果,你能发现什
么规律?
(1)
(2)
(3) .
探究
新知讲解
根据乘方的意义填空,观察计算结果,并根据你的观察回答下列问题:
(1)
(2)
(3) .
(1)上述三个乘法运算的乘数有什么共同的特征?
(2)它们的积都是什么形式?积的各个部分与乘数有什么关系?
(3)你能再举一个例子,使它具有上述三个乘法运算的乘数的共同特征吗?不写计算过程直接猜出它的运算结果.
新知讲解
猜想: am · an= (m、n都是正整数)
am+n
am · an =
(aa…a)
m个a
(aa…a)
n个a
(乘方的意义)
= aa…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
即
am · an = am+n (当m、n都是正整数)
猜想与证明
新知讲解
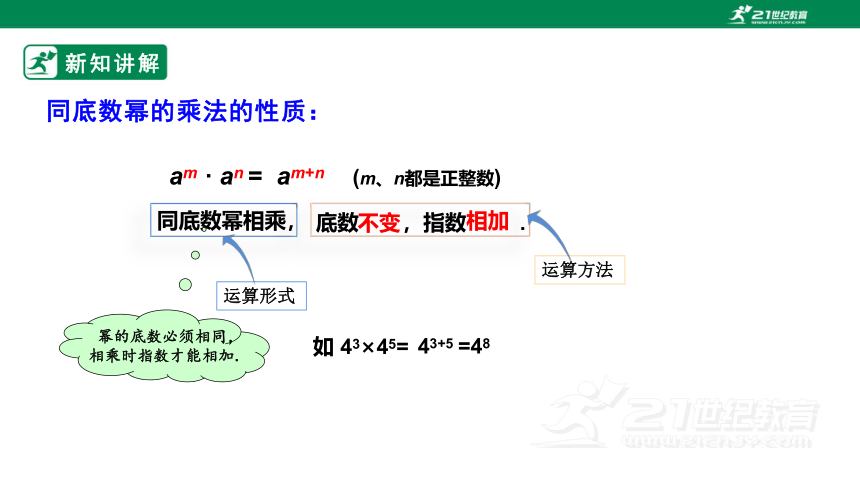
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 .
不变
相加
运算形式
运算方法
幂的底数必须相同,相乘时指数才能相加.
如 43×45=
43+5
=48
同底数幂的乘法的性质:
新知讲解
am·an·ap =
am+n+p
(m、n、p都是正整数)
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
想一想
同底数幂的乘法运算法则
am · an = am+n (m、n都是正整数) am·an·ap = am+n+p (m、n、p都是正整数)
强化练习
1、计算:
① 103×104; ② a·a3;
③ a·a3·a5; ④ x·x2+x2·x.
=107
=a4
=a9
=2x3
典例讲解
例1 计算:
(1) (2)
(3) (4)
(5)(b+2)3·(b+2)4·(b+2)
解: (1) x2·x5 =x2+5 =x 7.
(2) a·a6 =a1+6 =a7.
a=a1
(3) 原式=(-2)1+4+3 =(-2)8 =256
(4) xm·x3m+1=xm+3m+1 = x 4m+1.
(5) ( b+2)3·(b+2)4·(b+2)=(b+2)3+4+1=(b+2)8
思考:该式中相同的底数是多少?
-2
新知归纳
(-2)×(-2)4×(-2)3 ≠-21+4+3=-28 =-256
方法点拨
不要忽略指数是“1”的因式,如:a·a6≠a0+6 .
2. 底数是单项式,也可以是多项式,通常把底数看成一个整体来运算,如:
强化练习
2.计算:
① b2·b ② 10×102×103 ③ -a2·a6
=b3
=106
=-a8
④ y2n·yn+1 ⑤ -5·(-5)2·(-5)4
=y3n+1
=-57
3.判断:
① a5=a3+a2 ( )
② a5=a3·a2 ( )
③ am+n=am+an ( )
×
√
×
典例讲解
例2 已知:am=4, an=5.求am+n 的值.
分析: 把同底数幂的乘法法则逆运用,可以求出值.
解: am+n = am · an (逆运算)
=4 × 5
=20
强化练习
4.已知2x=3,2y=6,试写出2x+y的值.
解:2x+y
=2x×2y
=3×6
=18
课堂总结
学到了什么?
知识
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)(注:这个性质也适用于三个及三个以上的同底数幂相乘)
不变,
相加.
方法
“特殊→一般→特殊”
例子 公式 应用
易错点
(1)不要忽略指数是“1”的因式.
(2)底数可以是单项式,也可以是多项式,通常把底数看成一个整体来运算.
拓展提高
1. 计算:
(1)b5·b; (2)
(3)a2·a6 (4) y2n·yn+1
【课本P96 练习 】
拓展提高
提示:3x+2=3x·32=36,3x=4.
2. 若3x+2=36,则 .
2
3. 已知2a=2,2b=6,2c=18,试探求a,b,c之间的关系.
解:∵ 2b=6,∴2b · 2b=36,2a·2c=36,
2a·2c=2b · 2b ,
∴ 2a+c=22b,
∴ a+c=2b.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.1.1 同底数幂的乘法
人教版八年级上册
教学目标
1、理解同底数幂乘法的性质,并能进行简单的运算
2、在探索性质的过程中让学生经历观察、猜想、交流、验证、归纳总结的思维过程,让学生体会由特殊到一般再到特殊的思维方法和辩证的数学思想。
3、引导学生自主探索,体验成功的快乐,增强对数学学习的兴趣,在轻松、和谐有序的教学氛围中,培养学生的个性。
新知导入
一种电子计算机每秒可进行1千万亿(1015 ) 次运算,它工作103 s 可进行多少次运算?
列式:1015×103
怎样计算1015×103呢?
归纳:
底数相同的幂叫做同底数幂。
复习回顾
1、an 表示的意义是什么?其中a、n、an分别叫做什么
2、(-a)n 表示的意义是什么?底数、指数分别是什么?
3、10×10×10×10×10 可以写成________
意义:表示n个a相乘
a叫底数,n叫指数,an叫幂.
意义:表示n个-a相乘
-a叫底数,n叫指数,(-a)n叫幂.
105
新知讲解
根据乘方的意义可知
新知讲解
根据乘方的意义填空,观察计算结果,你能发现什
么规律?
(1)
(2)
(3) .
探究
新知讲解
根据乘方的意义填空,观察计算结果,并根据你的观察回答下列问题:
(1)
(2)
(3) .
(1)上述三个乘法运算的乘数有什么共同的特征?
(2)它们的积都是什么形式?积的各个部分与乘数有什么关系?
(3)你能再举一个例子,使它具有上述三个乘法运算的乘数的共同特征吗?不写计算过程直接猜出它的运算结果.
新知讲解
猜想: am · an= (m、n都是正整数)
am+n
am · an =
(aa…a)
m个a
(aa…a)
n个a
(乘方的意义)
= aa…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
即
am · an = am+n (当m、n都是正整数)
猜想与证明
新知讲解
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 .
不变
相加
运算形式
运算方法
幂的底数必须相同,相乘时指数才能相加.
如 43×45=
43+5
=48
同底数幂的乘法的性质:
新知讲解
am·an·ap =
am+n+p
(m、n、p都是正整数)
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
想一想
同底数幂的乘法运算法则
am · an = am+n (m、n都是正整数) am·an·ap = am+n+p (m、n、p都是正整数)
强化练习
1、计算:
① 103×104; ② a·a3;
③ a·a3·a5; ④ x·x2+x2·x.
=107
=a4
=a9
=2x3
典例讲解
例1 计算:
(1) (2)
(3) (4)
(5)(b+2)3·(b+2)4·(b+2)
解: (1) x2·x5 =x2+5 =x 7.
(2) a·a6 =a1+6 =a7.
a=a1
(3) 原式=(-2)1+4+3 =(-2)8 =256
(4) xm·x3m+1=xm+3m+1 = x 4m+1.
(5) ( b+2)3·(b+2)4·(b+2)=(b+2)3+4+1=(b+2)8
思考:该式中相同的底数是多少?
-2
新知归纳
(-2)×(-2)4×(-2)3 ≠-21+4+3=-28 =-256
方法点拨
不要忽略指数是“1”的因式,如:a·a6≠a0+6 .
2. 底数是单项式,也可以是多项式,通常把底数看成一个整体来运算,如:
强化练习
2.计算:
① b2·b ② 10×102×103 ③ -a2·a6
=b3
=106
=-a8
④ y2n·yn+1 ⑤ -5·(-5)2·(-5)4
=y3n+1
=-57
3.判断:
① a5=a3+a2 ( )
② a5=a3·a2 ( )
③ am+n=am+an ( )
×
√
×
典例讲解
例2 已知:am=4, an=5.求am+n 的值.
分析: 把同底数幂的乘法法则逆运用,可以求出值.
解: am+n = am · an (逆运算)
=4 × 5
=20
强化练习
4.已知2x=3,2y=6,试写出2x+y的值.
解:2x+y
=2x×2y
=3×6
=18
课堂总结
学到了什么?
知识
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)(注:这个性质也适用于三个及三个以上的同底数幂相乘)
不变,
相加.
方法
“特殊→一般→特殊”
例子 公式 应用
易错点
(1)不要忽略指数是“1”的因式.
(2)底数可以是单项式,也可以是多项式,通常把底数看成一个整体来运算.
拓展提高
1. 计算:
(1)b5·b; (2)
(3)a2·a6 (4) y2n·yn+1
【课本P96 练习 】
拓展提高
提示:3x+2=3x·32=36,3x=4.
2. 若3x+2=36,则 .
2
3. 已知2a=2,2b=6,2c=18,试探求a,b,c之间的关系.
解:∵ 2b=6,∴2b · 2b=36,2a·2c=36,
2a·2c=2b · 2b ,
∴ 2a+c=22b,
∴ a+c=2b.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
