数学人教A版2019选择性必修第一册3.2.1双曲线及其标准方程(共36张ppt)
文档属性
| 名称 | 数学人教A版2019选择性必修第一册3.2.1双曲线及其标准方程(共36张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 15:59:48 | ||
图片预览









文档简介
(共36张PPT)
直线
3.2.1 双曲线及其标准方程
复习引入
l
双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定位等都要用到双曲线的性质.本节我们将类比椭圆的研究方法研究双曲线的有关问题.
l
我们知道,平面内与两个定点
的距离的和等于常数(大于)的点的轨迹是一个椭圆.一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?下面我们先用信息技术探究一下.
新知探索
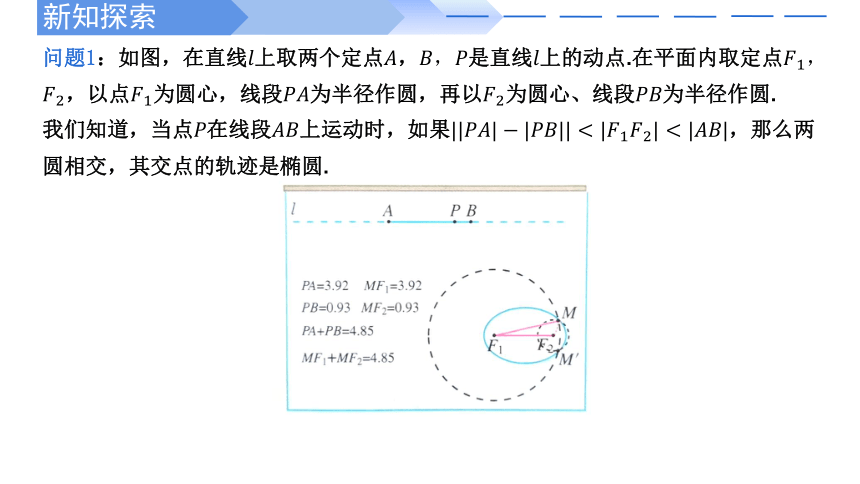
问题1:如图,在直线上取两个定点,是直线上的动点.在平面内取定点,,以点为圆心,线段为半径作圆,再以为圆心、线段为半径作圆.
我们知道,当点在线段上运动时,如果,那么两圆相交,其交点的轨迹是椭圆.
l
新知探索
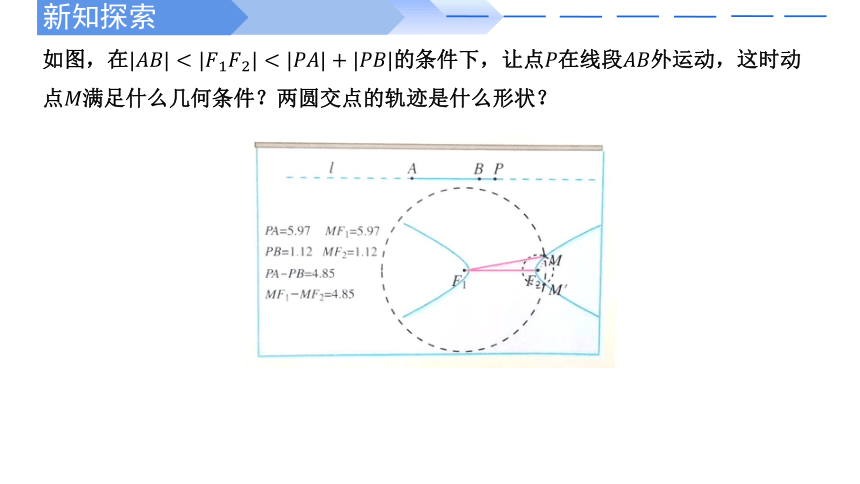
如图,在的条件下,让点在线段外运动,这时动点满足什么几何条件?两圆交点的轨迹是什么形状?
l
新知探索
如图,在的条件下,让点在线段外运动,这时动点满足什么几何条件?两圆交点的轨迹是什么形状?
l
新知探索
我们发现,在的条件下,点在线段外运动时,当点靠近定点时,;当点靠近定点时,.总之,点与两个定点,距离的差的绝对值是一个常数().这时,两圆交点的轨迹是不同于椭圆的曲线,它分左右两支.
l
一般地,我们把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
l
新知探索
问题2:类比求椭圆标准方程的过程,我们如何建立适当的坐标系,得出双曲线的方程?
l
观察我们画出的双曲线,发现它也具有对称性,而且直线是它的一条对称轴,所以我们取经过两焦点和的直线为轴,线段的垂直平分线为轴,建立如图所示的平面直角坐标系.设是双曲线上任意一点,双曲线的焦距为,那么,焦点,的坐标分别是,,又设(为大于的常数,).
新知探索
l
由双曲线的定义,双曲线就是下列点的集合:
因为,
所以①
类比椭圆标准方程的化简过程,化简①,得
两边同时除以,得
由双曲线得定义知,,即,所以.
类比椭圆标准方程的建立过程,令,其中,代入上式,
得.②
新知探索
l
从上述过程可以看到,双曲线上任意一点的坐标都是方程②的解,以方程②的解为坐标的点与双曲线的两个焦点,的距离之差的绝对值都为即以方程②的解为坐标的点都在双曲线上.
我们称方程是双曲线的方程,这个方程叫做双曲线的标准方程.它表示焦点在轴上,焦点分别是,的双曲线,这里.
新知探索
思考1:类比焦点在轴上的椭圆标准方程,焦点在轴上的双曲线的把标准方程是什么?
l
如图,双曲线的焦距为,焦点,的坐标分别是,,的意义同上,这时双曲线的方程是,这个方程也是双曲线的标准方程.
新知探索
答案:×,×,√.
辨析1.判断正误.
(1)在双曲线标准方程中,,,且.( )
(2)方程表示焦点在轴上的双曲线.( )
(3)方程表示双曲线.( )
新知探索
答案:C.
辨析2.(1)若动点到点,的距离之差的绝对值为,则点的轨迹是( ).
A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
答案:C.
辨析2.(2)已知双曲线的,,则该双曲线的标准方程为( ).
A. B.
C.或D.或
例析
例1.已知双曲线的两个焦点分别为,,双曲线上一点与,的距离差的绝对值等于,求双曲线的标准方程.
l
解:由于椭圆的焦点在轴上,所以设它的标准方程为.
由得又,
因此
所以,双曲线的标准方程为.
例析
例2.已知,两地相距,在地听到炮弹爆炸声比在地晚,且声速为,求炮弹爆炸点的轨迹方程.
l
解:如图,建立平面直角坐标系,使两点在轴上,并且原点与线段的中点重合.
设炮弹爆炸点的坐标为,
则,即.
又,所以,,.
所以,炮弹爆炸点的轨迹方程为
因为,所以点的轨迹是双曲线的右支,因此
新知探索
l
利用两个不同的观测点测得同一点发出信号的时间差,可以确定点所在双曲线的方程.如果再增设一个观测点,利用(或)两处测得的点发出信号的时间差,就可以确定点所在另一双曲线的方程.解这两个方程组成的方程组就能确定点的准确位置,这是双曲线的一个重要应用.
问题3:如图,点的坐标分别是,直线相交于点,且它们的斜率之积是,试求点的轨迹方程,并由点的轨迹方程判断轨迹的形状,与例比较,你有什么发现?
新知探索
l
问题3:如图,点的坐标分别是,直线相交于点,且它们的斜率之积是,试求点的轨迹方程.
化简整理,得
因此,点的轨迹是焦点在轴上的双曲线(除两点外).
解:设则,.
由题意知,即
回顾
3.1例3.如图,在,两点的坐标分别为,.直线相交于点,且它们的斜率之积是,求点的轨迹方程.
l
解:设点的坐标为,因为点的坐标为,
所以直线的斜率为
同理,直线的斜率为
由已知,有,
化简,得点的轨迹方程为.
点的轨迹是除去两点的椭圆.
新知探索
l
规律总结:若一个动点与两个定点连线的斜率之积为一个常数.
则当时,轨迹为双曲线(除,两点外),方程为;
当时,轨迹为椭圆(除,两点外),方程为;
当时,轨迹为圆(除两点外),方程为.
练习
题型一:双曲线的定义及应用
例1.若,是双曲线的两个焦点.
(1)若双曲线上一点到它的一个焦点的距离等于,求点到另一个焦点的距离;
(2)若点是双曲线上的一点,且,求的面积.
由定义和余弦定理得,,
,
解:(1)设,根据双曲线的定义知,
即,解得或
(2)由,得
∴,∴
∴
练习
方法技巧:
1.求双曲线上一点到某一焦点的距离时,若已知该点的横、纵坐标,则根据两点间距离公式可求出结果;若已知该点到另一焦点的距离,则根据求解,注意对所求结果进行必要的验证(负数应该舍去,且所求距离应该不小于
).
2.在解决双曲线中与焦点三角形有关的问题时,首先要注意定义中的条件的应用,其次要利用余弦定理、勾股定理或三角形面积公式等知识进行运算,在运算中要注意整体思想和一些变形技巧的应用.
练习
变1.已知双曲线的左、右焦点分别为,,为双曲线的右支上一点,且,则的面积等于__________.
解:在中,,,,
如图,过作于于,则为的中点,且,
∴,∴.
又∵为双曲线的右支上一点,∴∴
∴由条件知,.
练习
题型二:方程表示双曲线的条件
例2.如果方程表示双曲线,那么实数的取值范围是().
A. B.或 C. D.或
∴解得或.
答案:D.
解:∵方程表示双曲线,
练习
方法技巧:
将双曲线的方程化为标准方程的形式,假如双曲线的方程为,则当时,方程表示双曲线.
若则方程表示焦点在轴上的双曲线;
若则方程表示焦点在轴上的双曲线.
练习
变2.若曲线表示双曲线,则的取值范围是().
A. B. C.D.
答案:C.
解得.
则有,
解:根据题意,若曲线表示双曲线,
练习
题型三:双曲线标准方程的求法
例3.根据下列条件求双曲线的标准方程.
(1)求以椭圆的短轴的两个端点为焦点,且过点的双曲线的标准方程;
设双曲线的标准方程为,
解:法一.(待定系数法)
由题意知双曲线的两焦点,.
将点代入双曲线方程得,又,解得,.
所以双曲线的标准方程为.
练习
题型三:双曲线标准方程的求法
例3.根据下列条件求双曲线的标准方程.
(1)求以椭圆的短轴的两个端点为焦点,且过点的双曲线的标准方程;
即双曲线的标准方程为.
解:法二.(定义法)
由题意知双曲线的两焦点,.
且点在双曲线上,则
∴∴.
练习
(2)已知双曲线通过,两点,求双曲线的标准方程.
∵在双曲线上,
解:法一.若焦点在轴上,设双曲线的标准方程为
若焦点在轴上,设双曲线的标准方程为
∴解得
同理有解得(不符题意,舍去)
综上,双曲线的标准方程为
练习
(2)已知双曲线通过,两点,求双曲线的标准方程.
将点代入上述方程,得
解:法二.设所求双曲线的方程为
∴解得
所以所求双曲线的标准方程为
练习
方法技巧:
1.求双曲线标准方程的步骤
(1)是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
(2)是指确定,的数值,常由条件列出方程组求解.
2.双曲线标准方程的两种求法
(1)根据双曲线的定义得到相应的,,,再写出双曲线的标准方程.
(2)待定系数法:先设出双曲线的标准方程或(均为正数),然后根据条件求出待定的系数代入方程即可.
练习
变3.如图,已知双曲线以长方形的顶点为左、右焦点,且过两顶点.若,,求此双曲线的标准方程.
解:设双曲线的标准方程为.
∴双曲线得标准方程为.
∴解得
由题意,得.
练习
题型四:与双曲线有关的轨迹问题
例4.在中,已知,且三个内角满足,建立适当的坐标系,求顶点的轨迹方程.
解:以边所在的直线为轴,的垂直平分线为轴,建立平面直角坐标系,如图所示,则,.
由正弦定理,得,(为的外接圆半径).
∵,
∴,即,从而有.
练习
题型四:与双曲线有关的轨迹问题
例4.在中,已知,且三个内角满足,建立适当的坐标系,求顶点的轨迹方程.
由双曲线的定义知,点的轨迹为双曲线的右支(除去与轴的交点)
∵,,∴
即所求轨迹方程为.
练习
方法技巧:
求与双曲线有关的轨迹问题的方法
(1)列出等量关系,化简得到方程.
(2)寻找几何关系,由双曲线的定义,得出对应的方程.
[提醒](1)分清双曲线的焦点所在的坐标轴是哪个.
(2)检验所求的轨迹对应的是双曲线的一支还是两支.
练习
变4.已知圆和圆,动圆同时与圆及圆相外切,求动圆圆心的轨迹方程.
解:如图所示,设动圆与圆及圆分别外切于点和,
这表明动点与两定点的距离的差为常数,且.
∵,∴
根据两圆外切的条件,得,.
根据双曲线的定义,动点的轨迹为双曲线的左支,
则,∴.
因此所求动点的轨迹方程为.
课堂小结
1.双曲线的定义:
(1)定义:平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.
(2)焦点:两个定点叫做双曲线的焦点.
(3)焦距:两焦点间的距离叫做双曲线的焦距.
(4)双曲线就是下列点的集合:
[注]:平面内与两个定点的距离的差的绝对值等于非零常数,即,关键词“平面内”.
当时,轨迹是双曲线;当时,轨迹是分别以,为端点的两条射线;当时,轨迹不存在.
作业
(1)整理本节课的题型;
(2)课本P121的练习1——4题;
(3)课本P127习题3.2第1、2、5、6、7题.
直线
3.2.1 双曲线及其标准方程
复习引入
l
双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定位等都要用到双曲线的性质.本节我们将类比椭圆的研究方法研究双曲线的有关问题.
l
我们知道,平面内与两个定点
的距离的和等于常数(大于)的点的轨迹是一个椭圆.一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?下面我们先用信息技术探究一下.
新知探索
问题1:如图,在直线上取两个定点,是直线上的动点.在平面内取定点,,以点为圆心,线段为半径作圆,再以为圆心、线段为半径作圆.
我们知道,当点在线段上运动时,如果,那么两圆相交,其交点的轨迹是椭圆.
l
新知探索
如图,在的条件下,让点在线段外运动,这时动点满足什么几何条件?两圆交点的轨迹是什么形状?
l
新知探索
如图,在的条件下,让点在线段外运动,这时动点满足什么几何条件?两圆交点的轨迹是什么形状?
l
新知探索
我们发现,在的条件下,点在线段外运动时,当点靠近定点时,;当点靠近定点时,.总之,点与两个定点,距离的差的绝对值是一个常数().这时,两圆交点的轨迹是不同于椭圆的曲线,它分左右两支.
l
一般地,我们把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
l
新知探索
问题2:类比求椭圆标准方程的过程,我们如何建立适当的坐标系,得出双曲线的方程?
l
观察我们画出的双曲线,发现它也具有对称性,而且直线是它的一条对称轴,所以我们取经过两焦点和的直线为轴,线段的垂直平分线为轴,建立如图所示的平面直角坐标系.设是双曲线上任意一点,双曲线的焦距为,那么,焦点,的坐标分别是,,又设(为大于的常数,).
新知探索
l
由双曲线的定义,双曲线就是下列点的集合:
因为,
所以①
类比椭圆标准方程的化简过程,化简①,得
两边同时除以,得
由双曲线得定义知,,即,所以.
类比椭圆标准方程的建立过程,令,其中,代入上式,
得.②
新知探索
l
从上述过程可以看到,双曲线上任意一点的坐标都是方程②的解,以方程②的解为坐标的点与双曲线的两个焦点,的距离之差的绝对值都为即以方程②的解为坐标的点都在双曲线上.
我们称方程是双曲线的方程,这个方程叫做双曲线的标准方程.它表示焦点在轴上,焦点分别是,的双曲线,这里.
新知探索
思考1:类比焦点在轴上的椭圆标准方程,焦点在轴上的双曲线的把标准方程是什么?
l
如图,双曲线的焦距为,焦点,的坐标分别是,,的意义同上,这时双曲线的方程是,这个方程也是双曲线的标准方程.
新知探索
答案:×,×,√.
辨析1.判断正误.
(1)在双曲线标准方程中,,,且.( )
(2)方程表示焦点在轴上的双曲线.( )
(3)方程表示双曲线.( )
新知探索
答案:C.
辨析2.(1)若动点到点,的距离之差的绝对值为,则点的轨迹是( ).
A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
答案:C.
辨析2.(2)已知双曲线的,,则该双曲线的标准方程为( ).
A. B.
C.或D.或
例析
例1.已知双曲线的两个焦点分别为,,双曲线上一点与,的距离差的绝对值等于,求双曲线的标准方程.
l
解:由于椭圆的焦点在轴上,所以设它的标准方程为.
由得又,
因此
所以,双曲线的标准方程为.
例析
例2.已知,两地相距,在地听到炮弹爆炸声比在地晚,且声速为,求炮弹爆炸点的轨迹方程.
l
解:如图,建立平面直角坐标系,使两点在轴上,并且原点与线段的中点重合.
设炮弹爆炸点的坐标为,
则,即.
又,所以,,.
所以,炮弹爆炸点的轨迹方程为
因为,所以点的轨迹是双曲线的右支,因此
新知探索
l
利用两个不同的观测点测得同一点发出信号的时间差,可以确定点所在双曲线的方程.如果再增设一个观测点,利用(或)两处测得的点发出信号的时间差,就可以确定点所在另一双曲线的方程.解这两个方程组成的方程组就能确定点的准确位置,这是双曲线的一个重要应用.
问题3:如图,点的坐标分别是,直线相交于点,且它们的斜率之积是,试求点的轨迹方程,并由点的轨迹方程判断轨迹的形状,与例比较,你有什么发现?
新知探索
l
问题3:如图,点的坐标分别是,直线相交于点,且它们的斜率之积是,试求点的轨迹方程.
化简整理,得
因此,点的轨迹是焦点在轴上的双曲线(除两点外).
解:设则,.
由题意知,即
回顾
3.1例3.如图,在,两点的坐标分别为,.直线相交于点,且它们的斜率之积是,求点的轨迹方程.
l
解:设点的坐标为,因为点的坐标为,
所以直线的斜率为
同理,直线的斜率为
由已知,有,
化简,得点的轨迹方程为.
点的轨迹是除去两点的椭圆.
新知探索
l
规律总结:若一个动点与两个定点连线的斜率之积为一个常数.
则当时,轨迹为双曲线(除,两点外),方程为;
当时,轨迹为椭圆(除,两点外),方程为;
当时,轨迹为圆(除两点外),方程为.
练习
题型一:双曲线的定义及应用
例1.若,是双曲线的两个焦点.
(1)若双曲线上一点到它的一个焦点的距离等于,求点到另一个焦点的距离;
(2)若点是双曲线上的一点,且,求的面积.
由定义和余弦定理得,,
,
解:(1)设,根据双曲线的定义知,
即,解得或
(2)由,得
∴,∴
∴
练习
方法技巧:
1.求双曲线上一点到某一焦点的距离时,若已知该点的横、纵坐标,则根据两点间距离公式可求出结果;若已知该点到另一焦点的距离,则根据求解,注意对所求结果进行必要的验证(负数应该舍去,且所求距离应该不小于
).
2.在解决双曲线中与焦点三角形有关的问题时,首先要注意定义中的条件的应用,其次要利用余弦定理、勾股定理或三角形面积公式等知识进行运算,在运算中要注意整体思想和一些变形技巧的应用.
练习
变1.已知双曲线的左、右焦点分别为,,为双曲线的右支上一点,且,则的面积等于__________.
解:在中,,,,
如图,过作于于,则为的中点,且,
∴,∴.
又∵为双曲线的右支上一点,∴∴
∴由条件知,.
练习
题型二:方程表示双曲线的条件
例2.如果方程表示双曲线,那么实数的取值范围是().
A. B.或 C. D.或
∴解得或.
答案:D.
解:∵方程表示双曲线,
练习
方法技巧:
将双曲线的方程化为标准方程的形式,假如双曲线的方程为,则当时,方程表示双曲线.
若则方程表示焦点在轴上的双曲线;
若则方程表示焦点在轴上的双曲线.
练习
变2.若曲线表示双曲线,则的取值范围是().
A. B. C.D.
答案:C.
解得.
则有,
解:根据题意,若曲线表示双曲线,
练习
题型三:双曲线标准方程的求法
例3.根据下列条件求双曲线的标准方程.
(1)求以椭圆的短轴的两个端点为焦点,且过点的双曲线的标准方程;
设双曲线的标准方程为,
解:法一.(待定系数法)
由题意知双曲线的两焦点,.
将点代入双曲线方程得,又,解得,.
所以双曲线的标准方程为.
练习
题型三:双曲线标准方程的求法
例3.根据下列条件求双曲线的标准方程.
(1)求以椭圆的短轴的两个端点为焦点,且过点的双曲线的标准方程;
即双曲线的标准方程为.
解:法二.(定义法)
由题意知双曲线的两焦点,.
且点在双曲线上,则
∴∴.
练习
(2)已知双曲线通过,两点,求双曲线的标准方程.
∵在双曲线上,
解:法一.若焦点在轴上,设双曲线的标准方程为
若焦点在轴上,设双曲线的标准方程为
∴解得
同理有解得(不符题意,舍去)
综上,双曲线的标准方程为
练习
(2)已知双曲线通过,两点,求双曲线的标准方程.
将点代入上述方程,得
解:法二.设所求双曲线的方程为
∴解得
所以所求双曲线的标准方程为
练习
方法技巧:
1.求双曲线标准方程的步骤
(1)是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
(2)是指确定,的数值,常由条件列出方程组求解.
2.双曲线标准方程的两种求法
(1)根据双曲线的定义得到相应的,,,再写出双曲线的标准方程.
(2)待定系数法:先设出双曲线的标准方程或(均为正数),然后根据条件求出待定的系数代入方程即可.
练习
变3.如图,已知双曲线以长方形的顶点为左、右焦点,且过两顶点.若,,求此双曲线的标准方程.
解:设双曲线的标准方程为.
∴双曲线得标准方程为.
∴解得
由题意,得.
练习
题型四:与双曲线有关的轨迹问题
例4.在中,已知,且三个内角满足,建立适当的坐标系,求顶点的轨迹方程.
解:以边所在的直线为轴,的垂直平分线为轴,建立平面直角坐标系,如图所示,则,.
由正弦定理,得,(为的外接圆半径).
∵,
∴,即,从而有.
练习
题型四:与双曲线有关的轨迹问题
例4.在中,已知,且三个内角满足,建立适当的坐标系,求顶点的轨迹方程.
由双曲线的定义知,点的轨迹为双曲线的右支(除去与轴的交点)
∵,,∴
即所求轨迹方程为.
练习
方法技巧:
求与双曲线有关的轨迹问题的方法
(1)列出等量关系,化简得到方程.
(2)寻找几何关系,由双曲线的定义,得出对应的方程.
[提醒](1)分清双曲线的焦点所在的坐标轴是哪个.
(2)检验所求的轨迹对应的是双曲线的一支还是两支.
练习
变4.已知圆和圆,动圆同时与圆及圆相外切,求动圆圆心的轨迹方程.
解:如图所示,设动圆与圆及圆分别外切于点和,
这表明动点与两定点的距离的差为常数,且.
∵,∴
根据两圆外切的条件,得,.
根据双曲线的定义,动点的轨迹为双曲线的左支,
则,∴.
因此所求动点的轨迹方程为.
课堂小结
1.双曲线的定义:
(1)定义:平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.
(2)焦点:两个定点叫做双曲线的焦点.
(3)焦距:两焦点间的距离叫做双曲线的焦距.
(4)双曲线就是下列点的集合:
[注]:平面内与两个定点的距离的差的绝对值等于非零常数,即,关键词“平面内”.
当时,轨迹是双曲线;当时,轨迹是分别以,为端点的两条射线;当时,轨迹不存在.
作业
(1)整理本节课的题型;
(2)课本P121的练习1——4题;
(3)课本P127习题3.2第1、2、5、6、7题.
