人教版八年级上册 15.3 分式方程(第2课时) 课件(共40张PPT)
文档属性
| 名称 | 人教版八年级上册 15.3 分式方程(第2课时) 课件(共40张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 20:14:38 | ||
图片预览









文档简介
(共44张PPT)
人教版八年级数学上册第15章
15.3 分式方程
第2课时
课件说明
本课是在学生已经学习了分式方程解法的基础上,
进一步探索在实际问题中,如何将等量关系用分
式方程表示,从而利用分式方程解决实际问题.
教学目标:
1、用列表法列分式方程、
解决现实情境中的问题。
2、体会数学模型的应用价值。
教学重点:利用列表法审明题意,
将实际问题转化为分式方程的数学模型。
教学难点:从有形的列表逐渐过渡到无形的列表
(脑中理清题意)找准等量关系。
学习目标
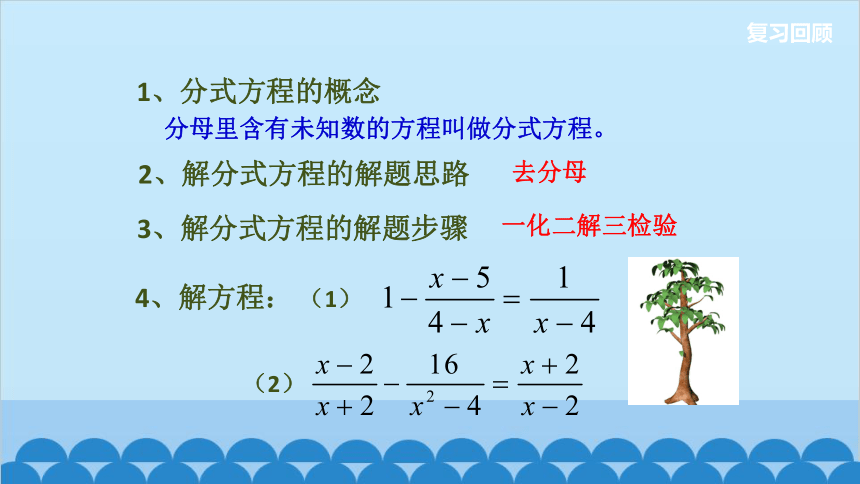
分母里含有未知数的方程叫做分式方程。
1、分式方程的概念
2、解分式方程的解题思路
一化二解三检验
去分母
3、解分式方程的解题步骤
4、解方程: (1)
(2)
复习回顾
2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。
速度×时间
静水速度 + 水流速度
静水速度-水流速度
1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________
工作效率×工作时间
复习回顾
甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用的时间相等,求甲、乙每小时各做多少个零件?
请审题分析题意设元
新课导入
解:设甲每小时做x个零件,则乙每小时做(x-6)个零件,依题意得:
经检验x=18是原分式方程的解,且符合题意.
答:甲每小时做18个,乙每小时做12个.
我们所列的是一个分式方程,这是分式方程的应用
由x=18得x-6=12
解得
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出方程.
4.解:认真仔细解这个分式方程.
5.验:检验.
6.答:注意单位和语言完整.
问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?
区别:解方程后要检验
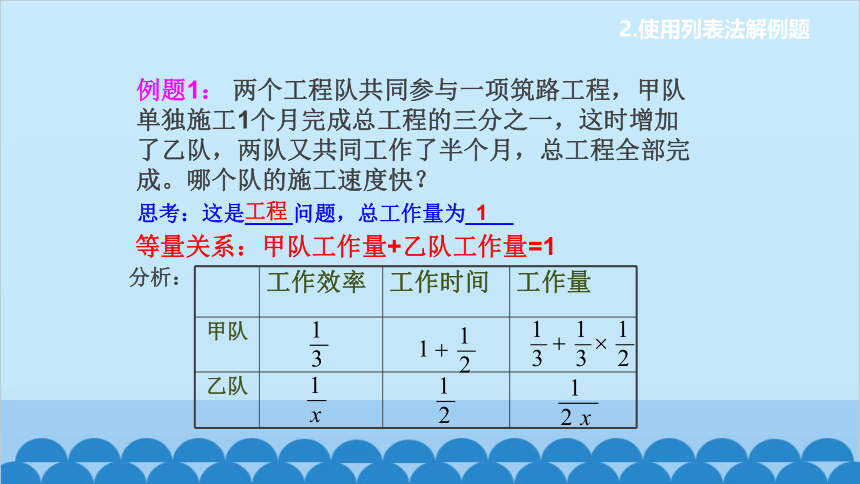
例题1: 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作效率 工作时间 工作量
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
2.使用列表法解例题
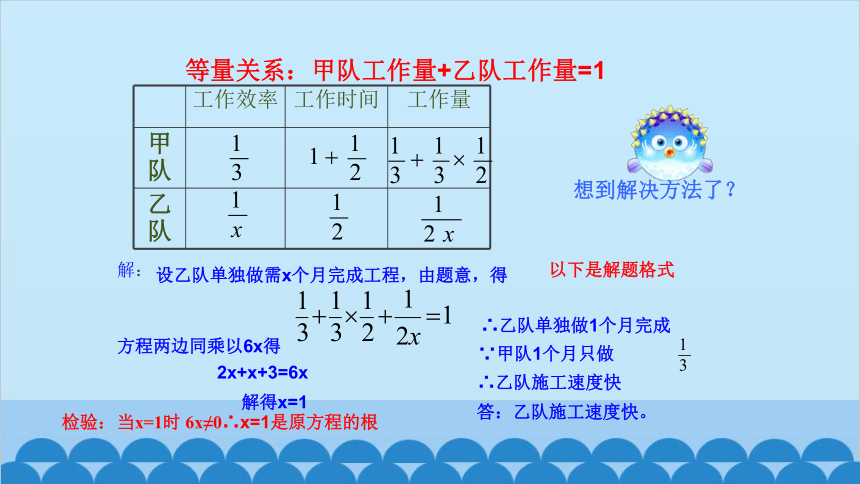
等量关系:甲队工作量+乙队工作量=1
解:
设乙队单独做需x个月完成工程,由题意,得
解得x=1
当x=1时 6x≠0∴x=1是原方程的根
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
想到解决方法了?
以下是解题格式
工作效率 工作时间 工作量
甲队
乙队
方程两边同乘以6x得
2x+x+3=6x
检验:
例2 某列车平均提速v km/h,用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少?
分析:这里的v,s表示已知数据,设提速前列车的平均速度为x km/h,先考虑下面的填空:
提速前列车行驶s km所用的时间为 h,提速后列车的平均速度为 km/h,提速后列车运行 km
所用时间为 h. 根据行驶时间的等量关系可以列出
方程:
(x+v)
(s+50)
x+v
s+50
路程km 速度km/h 时间h
提速前
提速后
等量关系:时间相等
可列方程:
去分母得:s(x+v)=x (s+50)
去括号,得
sx+sv=sx+50x.
移项、合并同类项,得
50x=xv.
解得
检验:由于v,s都是正数, 时x(x+v)≠0,
是原分式方程的解.
答:提速前列车的平均速度为 km/h.
解:
设提速前列车的平均速度为x千米/时由题意得
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
3.随时小结
练习1、 A、B两种机器人都被用来搬运化工原料,A型 机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
分析:(列表)
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
等量关系:时间相等
思考:这是____问题,三个工作量为____________________
工程
工作量、工作效率、工作时间
4.小组合作完成练习
解:
等量关系:时间相等
设A种机器人每小时搬运x kg,由题意得
=
解得x=90
检验:当x=90时,x(x-30)≠0
∴ x=90是原方程的根
∴ x-30=60
答:A和B两种机器人每小时分别能搬90kg和60kg。
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
以下是解题格式
在方程两边都乘以x(x-30)得
900(x-30)=600x
练习2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
工作效率 工作时间 完成的工作量
甲
乙
思考:这是____问题
工程
等量关系:甲完成的工作量+乙完成的工作量=总工作量
4.小组合作完成练习
工作效率 工作时间 完成的工作量
甲
乙
等量关系:甲完成的工作量+乙完成的工作量=总做总量
解:
设规定日期是x天,由题意,得
解得x=
答:规定日期是6天。
检验:当x=6时,x(x+3)≠0
∴ x=6是原方程的根
在方程两边都乘以x(x+3)得:
2(x+3)+x=x(x+3)
练习3、八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
思考:这是____问题,三个量为______________
行程
路程、速度、时间
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
4.小组合作完成练习
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
解:
设骑车同学的速度为x千米/时,由题意,得
解得x=15
答:骑车同学的速度为15千米/时。
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
检验:当x=15时,2x≠0
∴ x=15是原方程的根
在方程两边都乘以2x得:
60-30=2x
练习4、甲、乙两人分别从相距目的地6千米和10千米的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20分到达目的地。求甲、乙的速度。
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
思考:这是____问题,三个工作量为______________
行程
路程、速度、时间
等量关系:乙用的时间-甲用的时间=20分钟= 小时
4.小组合作完成练习
解:
设甲的速度x千米/时,则乙的速度是3x千米/时由题意得
解得x=1.5
答:甲的速度4.5千米/时,乙的速度是6千米/时。
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
等量关系:乙用的时间-甲用的时间=20分钟= 小时
∴ 3x=4.5 ,4x=6
检验:当x=1.5时,12x≠0
∴ x=1.5是原方程的根
在方程两边都乘以12x得:
30-24=4x
等量关系:
第二组用的时间-第一组用的时间=15分钟
练习5、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
思考:这是____问题,三个工作量为_______________
行程
路程、速度、时间
4.小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是1.2x米/分由题意得
解得x=5
答:第一组的速度6米/分,第二组的速度是5米/分。
以下是解题格式
∴ 1.2x=6
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
等量关系:
第二组用的时间-第一组用的时间=15分钟
检验:当x=5时,12x≠0
∴ x=5是原方程的根
在方程两边都乘以12x得:
5400-4500=180x
等量关系:
第二组用的时间-第一组用的时间=t分钟
练习6、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
思考:这是____问题,三个工作量为__________________
行程
路程、速度、时间
4.小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是ax米/分由题意得
∴解得x=
以下是解题格式
∴ ax=
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
等量关系:
第二组用的时间-第一组用的时间=t分钟
∵at≠0
答:第一组的速度 米/分,第二组的速度是 米/分。
ah-h=atx
在方程两边都乘以ax得:
检验:当x= 时,ax≠0
∴ x= 是原方程的根
2、老师小结:列表法可以方便理解解应用题。列表是一种手段而不是目的,平常做应用题可在心中自有一张表格,逐项理清,而不必都要列在纸上。
1、学生小结(心情、知识点、疑惑处等)
小结
【跟踪训练】
解:设自行车的速度为x km/h,那么汽车的速度是3x km/h, 依题意得:
汽车所用的时间=自行车所用时间-
可解得x=15.
经检验,x=15是原方程的解,并符合题意,
由x=15得3x=45.
答:自行车的速度是15 km/h,汽车的速度是45 km/h.
得到结果记住要检验.
2. 农机厂到距工厂15 km的向阳村检修农机,一部分人骑自行车先走,过了40 min,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
课堂练习
3.(绵阳·中考)在5月汛期,重庆某沿江村庄因洪
水而沦为孤岛.当时洪水流速为10 km/h,张师傅奉命
用冲锋舟去救援,他发现沿洪水顺流以最大速度航行2
km所用时间与以最大速度逆流航行1.2 km所用时间相
等.则该冲锋舟在静水中的最大航速为____.
【解析】设冲锋舟在静水中的最大航速为x km/h,根据题意
得 解得x=40,经检验x=40是所列方程的解.
答案:40 km/h
4.(珠海·中考)为了提高产品的附加值,某公司计划将研发生产的1 200件新产品进行精加工后再投放市场,现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
【解析】设甲工厂每天加工x件产品,则乙工厂每天加工
1.5x件产品,依题意得 ,
解得:x=40.
经检验x=40是原方程的解,所以1.5x=60.
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.
5.(潼南·中考)某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天
(2)若甲工程队独做a天后,再由甲、乙两工程队合作____天(用含a的代数式表示)可完成此项工程;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元
【解析】(1)设乙单独做x天完成此项工程,则甲单独做(x+30)天完成此项工程.
由题意得:20( )=1
整理得x2-10x-600=0,
解得x1=30,x2= -20.
经检验:x1=30,x2=-20都是分式方程的解,
但x2=-20不符合题意舍去.
x+30=60.
答:甲、乙两工程队单独完成此项工程各需要60天,30天.
(2)设甲单独做a天后,甲、乙再合作(20- )天,可以完成此项
工程.
(3)由题意得1×a+(1+2.5)(20- )≤64
解得a≥36
答:甲工程队至少要单独做36天后,再由甲、乙两队合作完成剩
下的工程,才能使施工费不超过64万元.
通过本课时的学习,需要我们
1.会列出分式方程解决简单的实际问题 ,并能根据实际问题的意义检验所得的结果是否合理.
2.掌握列分式方程解应用题的一般步骤:
(1)审:分析题意,找出数量关系和相等关系;
(2)设:直接设法与间接设法;
(3)列:根据等量关系,列出方程;
(4)解:解方程,得未知数的值;
(5)检:有两次检验.①是否是所列方程的解;②是否满足实际意义.
(6)答:注意单位和答案完整.
课堂小结
不要将过去看成是寂寞的,因为这是再也不会回头的。应想办法改善现在,因为那就是你,毫不畏惧地鼓起勇气向着未来前进。
—— 朗费罗
人教版八年级数学上册第15章
15.3 分式方程
第2课时
课件说明
本课是在学生已经学习了分式方程解法的基础上,
进一步探索在实际问题中,如何将等量关系用分
式方程表示,从而利用分式方程解决实际问题.
教学目标:
1、用列表法列分式方程、
解决现实情境中的问题。
2、体会数学模型的应用价值。
教学重点:利用列表法审明题意,
将实际问题转化为分式方程的数学模型。
教学难点:从有形的列表逐渐过渡到无形的列表
(脑中理清题意)找准等量关系。
学习目标
分母里含有未知数的方程叫做分式方程。
1、分式方程的概念
2、解分式方程的解题思路
一化二解三检验
去分母
3、解分式方程的解题步骤
4、解方程: (1)
(2)
复习回顾
2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。
速度×时间
静水速度 + 水流速度
静水速度-水流速度
1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________
工作效率×工作时间
复习回顾
甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用的时间相等,求甲、乙每小时各做多少个零件?
请审题分析题意设元
新课导入
解:设甲每小时做x个零件,则乙每小时做(x-6)个零件,依题意得:
经检验x=18是原分式方程的解,且符合题意.
答:甲每小时做18个,乙每小时做12个.
我们所列的是一个分式方程,这是分式方程的应用
由x=18得x-6=12
解得
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出方程.
4.解:认真仔细解这个分式方程.
5.验:检验.
6.答:注意单位和语言完整.
问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?
区别:解方程后要检验
例题1: 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作效率 工作时间 工作量
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
2.使用列表法解例题
等量关系:甲队工作量+乙队工作量=1
解:
设乙队单独做需x个月完成工程,由题意,得
解得x=1
当x=1时 6x≠0∴x=1是原方程的根
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
想到解决方法了?
以下是解题格式
工作效率 工作时间 工作量
甲队
乙队
方程两边同乘以6x得
2x+x+3=6x
检验:
例2 某列车平均提速v km/h,用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少?
分析:这里的v,s表示已知数据,设提速前列车的平均速度为x km/h,先考虑下面的填空:
提速前列车行驶s km所用的时间为 h,提速后列车的平均速度为 km/h,提速后列车运行 km
所用时间为 h. 根据行驶时间的等量关系可以列出
方程:
(x+v)
(s+50)
x+v
s+50
路程km 速度km/h 时间h
提速前
提速后
等量关系:时间相等
可列方程:
去分母得:s(x+v)=x (s+50)
去括号,得
sx+sv=sx+50x.
移项、合并同类项,得
50x=xv.
解得
检验:由于v,s都是正数, 时x(x+v)≠0,
是原分式方程的解.
答:提速前列车的平均速度为 km/h.
解:
设提速前列车的平均速度为x千米/时由题意得
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
3.随时小结
练习1、 A、B两种机器人都被用来搬运化工原料,A型 机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
分析:(列表)
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
等量关系:时间相等
思考:这是____问题,三个工作量为____________________
工程
工作量、工作效率、工作时间
4.小组合作完成练习
解:
等量关系:时间相等
设A种机器人每小时搬运x kg,由题意得
=
解得x=90
检验:当x=90时,x(x-30)≠0
∴ x=90是原方程的根
∴ x-30=60
答:A和B两种机器人每小时分别能搬90kg和60kg。
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
以下是解题格式
在方程两边都乘以x(x-30)得
900(x-30)=600x
练习2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
工作效率 工作时间 完成的工作量
甲
乙
思考:这是____问题
工程
等量关系:甲完成的工作量+乙完成的工作量=总工作量
4.小组合作完成练习
工作效率 工作时间 完成的工作量
甲
乙
等量关系:甲完成的工作量+乙完成的工作量=总做总量
解:
设规定日期是x天,由题意,得
解得x=
答:规定日期是6天。
检验:当x=6时,x(x+3)≠0
∴ x=6是原方程的根
在方程两边都乘以x(x+3)得:
2(x+3)+x=x(x+3)
练习3、八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
思考:这是____问题,三个量为______________
行程
路程、速度、时间
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
4.小组合作完成练习
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
解:
设骑车同学的速度为x千米/时,由题意,得
解得x=15
答:骑车同学的速度为15千米/时。
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
检验:当x=15时,2x≠0
∴ x=15是原方程的根
在方程两边都乘以2x得:
60-30=2x
练习4、甲、乙两人分别从相距目的地6千米和10千米的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20分到达目的地。求甲、乙的速度。
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
思考:这是____问题,三个工作量为______________
行程
路程、速度、时间
等量关系:乙用的时间-甲用的时间=20分钟= 小时
4.小组合作完成练习
解:
设甲的速度x千米/时,则乙的速度是3x千米/时由题意得
解得x=1.5
答:甲的速度4.5千米/时,乙的速度是6千米/时。
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
等量关系:乙用的时间-甲用的时间=20分钟= 小时
∴ 3x=4.5 ,4x=6
检验:当x=1.5时,12x≠0
∴ x=1.5是原方程的根
在方程两边都乘以12x得:
30-24=4x
等量关系:
第二组用的时间-第一组用的时间=15分钟
练习5、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
思考:这是____问题,三个工作量为_______________
行程
路程、速度、时间
4.小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是1.2x米/分由题意得
解得x=5
答:第一组的速度6米/分,第二组的速度是5米/分。
以下是解题格式
∴ 1.2x=6
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
等量关系:
第二组用的时间-第一组用的时间=15分钟
检验:当x=5时,12x≠0
∴ x=5是原方程的根
在方程两边都乘以12x得:
5400-4500=180x
等量关系:
第二组用的时间-第一组用的时间=t分钟
练习6、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
思考:这是____问题,三个工作量为__________________
行程
路程、速度、时间
4.小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是ax米/分由题意得
∴解得x=
以下是解题格式
∴ ax=
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
等量关系:
第二组用的时间-第一组用的时间=t分钟
∵at≠0
答:第一组的速度 米/分,第二组的速度是 米/分。
ah-h=atx
在方程两边都乘以ax得:
检验:当x= 时,ax≠0
∴ x= 是原方程的根
2、老师小结:列表法可以方便理解解应用题。列表是一种手段而不是目的,平常做应用题可在心中自有一张表格,逐项理清,而不必都要列在纸上。
1、学生小结(心情、知识点、疑惑处等)
小结
【跟踪训练】
解:设自行车的速度为x km/h,那么汽车的速度是3x km/h, 依题意得:
汽车所用的时间=自行车所用时间-
可解得x=15.
经检验,x=15是原方程的解,并符合题意,
由x=15得3x=45.
答:自行车的速度是15 km/h,汽车的速度是45 km/h.
得到结果记住要检验.
2. 农机厂到距工厂15 km的向阳村检修农机,一部分人骑自行车先走,过了40 min,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
课堂练习
3.(绵阳·中考)在5月汛期,重庆某沿江村庄因洪
水而沦为孤岛.当时洪水流速为10 km/h,张师傅奉命
用冲锋舟去救援,他发现沿洪水顺流以最大速度航行2
km所用时间与以最大速度逆流航行1.2 km所用时间相
等.则该冲锋舟在静水中的最大航速为____.
【解析】设冲锋舟在静水中的最大航速为x km/h,根据题意
得 解得x=40,经检验x=40是所列方程的解.
答案:40 km/h
4.(珠海·中考)为了提高产品的附加值,某公司计划将研发生产的1 200件新产品进行精加工后再投放市场,现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
【解析】设甲工厂每天加工x件产品,则乙工厂每天加工
1.5x件产品,依题意得 ,
解得:x=40.
经检验x=40是原方程的解,所以1.5x=60.
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.
5.(潼南·中考)某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天
(2)若甲工程队独做a天后,再由甲、乙两工程队合作____天(用含a的代数式表示)可完成此项工程;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元
【解析】(1)设乙单独做x天完成此项工程,则甲单独做(x+30)天完成此项工程.
由题意得:20( )=1
整理得x2-10x-600=0,
解得x1=30,x2= -20.
经检验:x1=30,x2=-20都是分式方程的解,
但x2=-20不符合题意舍去.
x+30=60.
答:甲、乙两工程队单独完成此项工程各需要60天,30天.
(2)设甲单独做a天后,甲、乙再合作(20- )天,可以完成此项
工程.
(3)由题意得1×a+(1+2.5)(20- )≤64
解得a≥36
答:甲工程队至少要单独做36天后,再由甲、乙两队合作完成剩
下的工程,才能使施工费不超过64万元.
通过本课时的学习,需要我们
1.会列出分式方程解决简单的实际问题 ,并能根据实际问题的意义检验所得的结果是否合理.
2.掌握列分式方程解应用题的一般步骤:
(1)审:分析题意,找出数量关系和相等关系;
(2)设:直接设法与间接设法;
(3)列:根据等量关系,列出方程;
(4)解:解方程,得未知数的值;
(5)检:有两次检验.①是否是所列方程的解;②是否满足实际意义.
(6)答:注意单位和答案完整.
课堂小结
不要将过去看成是寂寞的,因为这是再也不会回头的。应想办法改善现在,因为那就是你,毫不畏惧地鼓起勇气向着未来前进。
—— 朗费罗
